数据结构与算法——DFS(深度优先搜索)
算法介绍:
深度优先搜索(Depth-First Search,简称DFS)是一种用于遍历或搜索树或图的算法。这种算法会尽可能深地搜索图的分支,直到找到目标节点或达到叶节点(没有子节点的节点),然后回溯到上一个分支继续搜索。DFS可以用于许多问题,比如路径寻找、连通性验证、拓扑排序等。
在ACM、蓝桥杯等著名竞赛中DFS算法是比较重要的,特别是在蓝桥杯中每一年几乎都要考DFS/BFS算法。DFS算法在OI赛中用处非常大,可以通过DFS/BFS暴力的方式可以拿到部分分数,蓝桥杯一般可以拿到20%的分数,有的甚至高达50%,是暴力得分的不二之选。

基本步骤:
DFS通常使用递归或栈来实现。以下是DFS的基本步骤:
- 选择起始点:选择图中的一个点作为起始点。
- 访问节点:标记起始节点为已访问,并将该节点加入递归或栈中。
- 探索邻接节点:从该点周围取出一个点,检查它的所有未访问的邻接节点。
- 递归或迭代:对每个未访问的邻接节点,将其标记为已访问,然后将其推入递归或栈中。
- 回溯:当当前节点的所有邻接节点都被访问后,递归中回溯/从栈中弹出该节点,继续搜索上一个点的其他分支。
- 结束条件:当栈为空或找到目标节点时,搜索结束。
图解算法:
下面放一张我们学校ACM在大一培训时使用的一张动态BFS/DFS步骤图。注:红色遍历为BFS、黄色遍历为DFS。(绿色为起点,紫色为终点,黑色为障碍物)

由上图中我们可以看出,DFS的遍历为一条路,用我们学长的话说就是一条路走到头,找不到就再回头换另一条路,继续搜索,直到找到终点。那么BFS就是在一个点的周围每一个点都走一遍试一下,属于扩散型的。找不到的话在这个点的基础上再去扩散四周寻找。BFS一般通过栈来实现,DFS一般通过递归来实现。
下面我们将以3*3的网格,只考虑上下左右四个方向,上左、下左等四个方向不考虑,递归顺序为{上、下、左、右},顺序可按照自己的想法,这里以上下左右顺序为例,给大家模拟实现一下过程。
第一步:
本身就在起点,先把此时起点标记为已经走过了,即vis[起点]=true,告诉后面这个点不能再搜索了,不标记的话可能会陷入死循环。在寻找起点的上下左右格子,我们发现,{上}、{左}方向都已经超出了格子范围,在题中就是超出了下标范围,那么我们能考虑的就只有{下}、{右}方向,由于我们递归的顺序为{上、下、左、右},{上}方向超出了格子范围,那么级别最高且合法的就是{下}方向了,从起点向下走。
第二步:
先标记,vis[第一步]=true。此时我们发现{左}方向已经不在网格里面了,下标已经越界了,所以不考虑{左}方向,此时递归顺序为{上、下、右}方向,向上走,在第一步一开始我们就把vis[起点]标记为true,说明已经走过了,下面不允许走了,{上}方向也不能走了。此时优先级最高的为下方向了,下方向没有被标记过,所以可以走。

第三步:
还是先标记,把当前位置所走的标记为已经走过,即vis[第二步]=true。此时我们发现{左、下}两个方向已经越界了,所以不考虑,此时递归优先级为{上、右},由于第三步刚开始就把vis[第二步]=true,已经标记了,不能走了,所以这一步只能向右走。

第四步:
还还还是先标记,vis[第三步]=true。此时我们发现{下}方向已经越界了,所以不考虑{下}方向了,在这一步刚开始我们把{左}方向这个点已经给标记过了,所以不能走,那么剩余的合法递归顺序为{上、右},此时我们便可以向上走,找到终点,完成此次DFS(深度优先搜索)。

算法模板:
从上面的图解算法中步骤我们把算法步骤归结为一下:
首先我们需要一个数组即输入的数据数组,可能为int、也肯为char,在绝大部分题目中都需要一个标记数组,即bool类型的vis数组。然后在题目中找到搜索的起点跟终点,设置dfs函数的参数,根据题目的不同参数个数不同。在主函数dfs函数之前先把vis[起点]标记为true,一定不要忘记,否则就是死循环。确定了起点,把参数传给dfs函数参数,进入dfs递归函数,确定函数的终止条件,即当前状态==目标状态或者递归值==某个数等,终止条件一定在函数的最前面,否则会影响答案。再次,在当前点,寻找当前点的周围(根据题目,可能四个点,也可能八个点等),用for循环遍历每一个点,如果这个点已经被标记过了或者数组下标越界都是不合法的,直接continue掉。那么剩下的就是合法的,可以访问下一个点,先把下一个点给标记完再去递归下一个点,再进入dfs函数递归,注意大部分dfs都需要回溯的,即把vis[当前点]=false,为什么需要回溯,这就是我们所说的一条路走不通,回头换一条路走,那么我要回头,前面走过的已经被标记的,还咋走,那就要vis[当前点]=false解除标记。下面贴一个dfs函数的一般模板。
void dfs(int dep){//dep为当前状态if(dep==x){//当前状态==目标状态,终止条件更新结果return;}for(int i=0;i<n;i++){//遍历每一种可能if(不符合条件){continue;//跳过}//符合条件vis[访问的点]=true;//先标记dfs(下一个状态);vis[访问的点]=false;//恢复现场,大部分需要回溯,有的不需要这一步}
}算法例题:
现在各大算法刷题网站上dfs题目非常的多,dfs题目的变化也比较多,现在各种各样的题目层出不穷,博主所做过的题印象中大部分在终止条件哪里变化的比较多,像是还有在条件判断上增加附加条件等等,下面博主选取几个比较具有代表性的给大家讲解一下,加深理解一下dfs算法。
一、马走日
题目描述:
马在中国象棋以日字形规则移动。请编写一段程序,给定n×m大小的棋盘,以及马的初始位置(x,y),要求不能重复经过棋盘上的同一个点,计算马可以有多少途径遍历棋盘上的所有点。
输入
第一行为整数T(T < 10),表示测试数据组数。
每一组测试数据包含一行,为四个整数,分别为棋盘的大小以及初始位置坐标n,m,x,y。(0≤x≤n-1,0≤y≤m-1, m < 10, n < 10)。
输出
每组测试数据包含一行,为一个整数,表示马能遍历棋盘的途径总数,0为无法遍历一次。
输入示例
1
5 4 0 0
输出示例
32
解题思路:
这个题不同在了马走的方向跟之前走四个方向的不同他是斜着跳,与象棋上的马一样,例如(1,2)、(-2,1)等,初始状态就是起点(x,y),终点的话,除了起点每个点都可能是终点,这样不好确定终点,但是我们有一个条件,遍历完所有点,有两种方法可以确定遍历完所有点,第一种是n*m的棋盘,那么如果走完了n*m步就完成了一次,第二种设置一个标记数组,标记棋盘上每一个点都被标记完了就完成一次,很明显第一种方法比第二种好。由于统计的是途径总数,每完成一次计数就++,直到他无路可走,自动退出函数。
AC代码:
#include<iostream>
using namespace std;
int a[15][15],vis[15][15];
int n,m,sx,sy;
int ans;//途径数
int dx[]={1,1,-1,-1,2,2,-2,-2};//马在棋盘上可以跳八个方向
int dy[]={2,-2,2,-2,1,-1,1,-1};
void dfs(int x,int y,int dep){//(x,y)当前坐标,dep当前步数if(dep==n*m){//终止条件ans++;return;}for(int i=0;i<8;i++){//八个方向遍历int bx=x+dx[i];int by=y+dy[i];if(vis[bx][by]==1){//已经被标记过了continue;}if(bx<0||bx>=n||by<0||by>=m){//下标越界continue;}vis[bx][by]=1;//先标记该点dfs(bx,by,dep+1);//再去递归下一次vis[bx][by]=0;//回溯--解标记}
}
int main(){int t;cin>>t;while(t--){ans=0;scanf("%d%d%d%d",&n,&m,&sx,&sy);vis[sx][sy]=1;//起点标记dfs(sx,sy,1);printf("%d",ans);}return 0;
}二、AcWing 3428. 放苹果
把 M个同样的苹果放在 N个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?
盘子相对顺序不同,例如 5,1,1和 1,5,1算作同一种分法。
输入格式
输入包含多组测试数据。
每组数据占一行,包含两个整数 M 和 N。
输出格式
每组数据,输出一行一个结果表示分法数量。
数据范围
1≤M,N≤10;
输入样例:
7 3输出样例:
8
解题思路:
N与M最大只有10,dfs可以适用,M个苹果放到N个盘子里,允许盘子空着不放,可以直接dfs递归实现,我们设置两个参数,一个遍历的盘子数dep,一个遍历的苹果数sum,每一次向盘子里面放t个苹果,那么苹果数sum-t,盘子数sum+1,当超出了盘子数不符合条件或者苹果数<0则返回上一步执行。
AC代码:
#include<iostream>
using namespace std;int a[101]={1};//初始化为1放苹果的至少放一个
int m,n,num=0;//m:苹果,n:盘子void dfs(int sum,int dep){if(sum<0){//没有苹果就没法放了,回溯return;}if(sum==0&&dep<=n+1){//终止条件num++;return;}for(int i=a[dep-1];i<=m;i++){//防止重复放比如{1,5,1}跟{5,1,1}是一样的放法a[dep]=i;//放的个数dfs(sum-i,dep+1);//继续搜索下一个盘子//没有回溯,因为这是组合问题,分的苹果数重复了属于同一种}
}
int main(){while(scanf("%d%d",&m,&n)!=EOF){num=0;dfs(m,1);printf("%d\n",num);}return 0;
}三、八皇后问题
会下国际象棋的人都很清楚:皇后可以在横、竖、斜线上不限步数地吃掉其他棋子。
如何将 8 个皇后放在棋盘上(有 8×8 个方格),使它们谁也不能被吃掉!
这就是著名的八皇后问题。
已经知道 8 皇后问题一共有 92 组解。
要求打印每一种解。
解题思路:
对于八皇后问题以后博主感觉不会出类似的题,但是我还是想把八皇后加入到例题来讲解,因为它实在是太经典了。八皇后问题是最经典的递归问题,你可以说没学过八皇后,但是不能说学了dfs但是不会八皇后。为什么说八皇后问题最经典,八皇后问题的条件一般是不会改变的,它在标记这一块动了手脚,本来由标记一个点变为标记整行、整列、点所在的主对角线、点所在的副对角线。主要麻烦在了标记这一块,标记处理好了,回溯的时候也比较好处理,现在对于标记网上有很多方法,我看了很多方法找出了一种我认为比较好的方法,是acking老师讲解的方法,跟大家分享一下。
首先,它需要标记四条线,分别是行、列、上左到右下、上右到左下,把它简化一下,我每次遍历从第一行开始,每次向下一个,这样保证了每次行不一样,可以少标记一个数组。列的话,一个一维vis数组就够了,上左到右下这条线,把它顺时针旋转45°,会发现是竖直的线。每一条线满足i-j+n不一样(i,j)是坐标。上右到左下这条线逆时针旋转45°,也会发现是一条竖线,每一条线满足i+j是不一样的。这样可以把它们的值当作下标值处理。
视频讲解:acking老师讲解--->点击这里<---


代码实现:
#include<stdio.h>
int a[10][10];
int vis1[8]/*标记列*/, vis2[16],/*标记左上右下*/ vis3[16]/*标记右上左下*/;
int n = 8, ans = 0;
void vis(int i, int j, int flag) {a[i][j] = flag;vis1[j] = flag;vis2[i - j + n] = flag;vis3[i + j] = flag;
}
void dfs(int i) {if (i == n) {printf("No.%d\n", ++ans);for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {printf("%d ", a[i][j]);}printf("\n");}return;}for (int j = 0; j < n; j++) {if (vis1[j] == 0 && vis2[i - j + n] == 0 && vis3[i + j] == 0) {vis(i, j, 1);dfs(i + 1);vis(i, j, 0);}}
}
int main() {dfs(0);return 0;
}四、第十四届蓝桥杯省赛大学B组 岛屿个数
题目描述:
小蓝得到了一副大小为 M×N 的格子地图,可以将其视作一个只包含字符 0(代表海水)和 1(代表陆地)的二维数组,地图之外可以视作全部是海水,每个岛屿由在上/下/左/右四个方向上相邻的 1 相连接而形成。
在岛屿 A 所占据的格子中,如果可以从中选出 k 个不同的格子,使得他们的坐标能够组成一个这样的排列:(x0,y0),(x1,y1),...,(xk−1,yk−1),其中 (x(i+1)%k,y(i+1)%k) 是由 (xi,yi) 通过上/下/左/右移动一次得来的 (0≤i≤k−1),此时这 k 个格子就构成了一个 “环”。
如果另一个岛屿 B 所占据的格子全部位于这个 “环” 内部,此时我们将岛屿 B 视作是岛屿 A 的子岛屿。若 B 是 A 的子岛屿,C 又是 B 的子岛屿,那 C 也是 A 的子岛屿。
请问这个地图上共有多少个岛屿?在进行统计时不需要统计子岛屿的数目。
输入格式:
第一行一个整数 T,表示有 T 组测试数据。
接下来输入 T 组数据。
对于每组数据,第一行包含两个用空格分隔的整数 M、N 表示地图大小;接下来输入 M行,每行包含 N 个字符,字符只可能是 0 或 1。
输出格式:
对于每组数据,输出一行,包含一个整数表示答案。
数据范围:
对于 30% 的评测用例,1≤M,N≤10。
对于 100% 的评测用例,1≤T≤10,1≤M,N≤50。
解题思路:
这个题博主感觉是蓝桥杯出的比较成功的题,它考查的非常具有思维性,打破了传统的dfs思路。加入了新的判断条件,很具有挑战性,博主感觉以后的像蓝桥杯这种比赛,dfs的考察一定会向着这个方向发展,传统的dfs将会退出题海战术。具体的讲解跟AC代码,请看我这一篇文章,文章单独讲解了这一道题,由于文章长度限制这里不再详解,请移步下面链接。
第十四届省赛大学B组(C/C++)岛屿个数-CSDN博客文章浏览阅读1.1k次,点赞30次,收藏14次。这不是普通的DFS/BFS搜索题,看着很像最少连通块,但是题目中又有了新的定义就是在陆地环里面(被陆地包围)也算属于此外围岛屿,那么我们就也要判定这种环岛屿,博主的思路是先BFS也可DFS找出连通块的个数(四个方向),建一个vector把连通块的起点存进去,方便去找环岛屿,只要有一个起点(或者此连通块任意一个点),此连通块的点便可通过移动一网打尽,再BFS(或者DFS)判定该岛屿是否属于这种环岛屿,不属于就结果加一,属于就不用加。对于 100% 的评测用例,1≤T≤10,1≤M,N≤50。https://blog.csdn.net/m0_73633807/article/details/137248445?spm=1001.2014.3001.5501
感谢大家支持,下篇更新BFS(广度优先搜索)
相关文章:
数据结构与算法——DFS(深度优先搜索)
算法介绍: 深度优先搜索(Depth-First Search,简称DFS)是一种用于遍历或搜索树或图的算法。这种算法会尽可能深地搜索图的分支,直到找到目标节点或达到叶节点(没有子节点的节点),然后…...

基于lambda简化设计模式
写在文章开头 本文将演示基于函数式编程的理念,优化设计模式中繁琐的模板化编码开发,以保证用尽可能少的代码做尽可能多的事,希望对你有帮助。 Hi,我是 sharkChili ,是个不断在硬核技术上作死的 java coder ÿ…...

揭秘! 经纬恒润“车路云一体化”方案研发服务背后的科技驱动力
随着高级别智能驾驶技术的飞速发展,自动驾驶与路侧基础设施协同合作已成为行业内的又一热点。我国率先提出以“车路云一体化”为核心的战略布局,国家政策密集出台,地方试点积极推进,行业标准日趋完善,智能网联汽车“车…...

Redis操作--RedisTemplate(二)StringRedisTemplate
一、介绍 1、简介 由于存储在 Redis 中的 key 和 value 通常是很常见的 String 类型,Redis模块提供了 RedisConnection 和 RedisTemplate 的扩展,分是 StringRedisConnection 和 StringRedisTemplate,作为字符串操作的解决方案。 通过源码…...

【自动驾驶】ROS中自定义格式的服务通信,含命令行动态传参(c++)
目录 通信流程创建服务器端及客户端新建服务通讯文件修改service的xml及cmakelistCMakeLists.txt编辑 msg 相关配置编译消息相关头文件在cmakelist中包含头文件的路径在service包下编写service.cpp在client包下编写client.cpp测试运行查询服务的相关指令列出目前的所有服务&…...

优思学院|PDCA和DMAIC之间如何选择?
在现代组织中,提升方法、质量和效率是企业追求卓越、保持竞争力的核心目标。在这条道路上,DMAIC(定义、测量、分析、改进、控制)和PDCA(计划、执行、检查、行动)被广泛应用于持续改进和问题解决。这两者虽然…...

5 款最佳 Micro SD 卡恢复软件,助您恢复文件
您是否对数据恢复存在某些疑问,并想知道如何恢复 Micro SD 卡上的文件?如果是,那么在本文中您将找到答案。网上有许多专门用于从 Micro SD 卡或格式化的 Micro 卡恢复已删除文件而设计的软件。因此,在本文中,我们将向您…...

【使用教程】CiA402中的“原点回归模式”和“轮廓位置模式”搭配使用操作实例
使用“原点回归模式”配合“轮廓位置模式”是步进或伺服电机使用过程中最常用的方法,其对于提高自动化生产线的准确性和效率具有重要意义,本文将对正常使用控制电机中发送的命令及顺序进行简要说明。 说明:“原点回归”以“堵转回原点”的方式…...

服务器网络不通排查方案
服务器网络不通排查方案 最近遇到了服务器上服务已经启动,但是在浏览器上无法访问的问题,记录一下排查流程 文章目录 服务器网络不通排查方案netstart排查网络连接信息netstat 命令netstat -aptn 命令 iptables总结 netstart排查网络连接信息 netstat …...
问题解决历程)
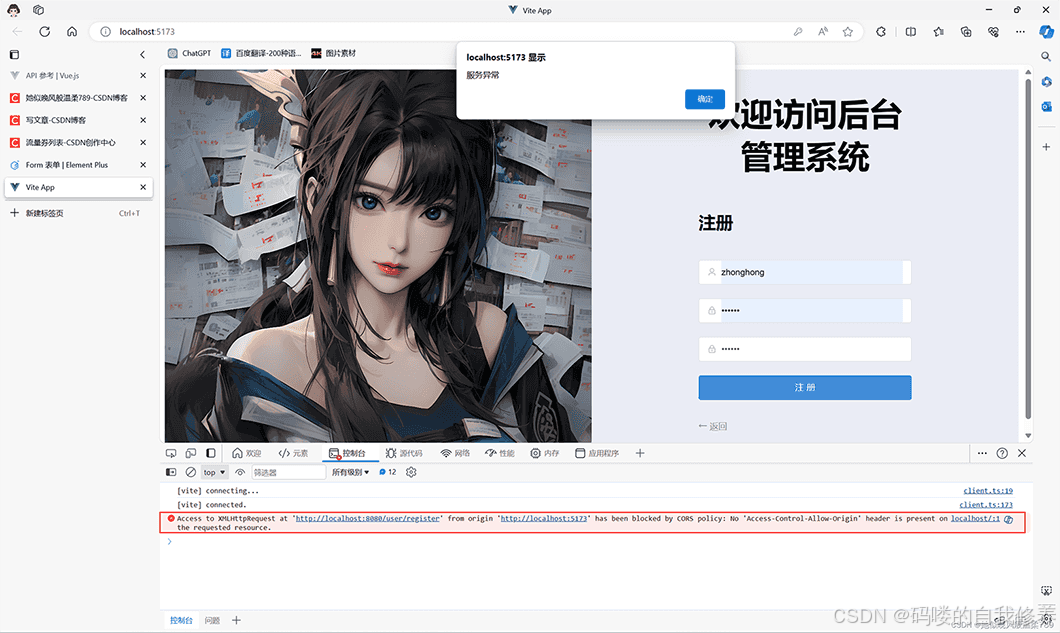
Spring Boot + Vue 跨域配置(CORS)问题解决历程
在使用 Spring Boot 和 Vue 开发前后端分离的项目时,跨域资源共享(CORS)问题是一个常见的挑战。接下来,我将分享我是如何一步步解决这个问题的,包括中间的一些试错过程,希望能够帮助到正在经历类似问题的你…...
Think | 大模型迈向AGI的探索和对齐
注:节选自我于24年初所写的「融合RL与LLM思想探寻世界模型以迈向AGI」散文式风格文章,感兴趣的小伙伴儿可以访问我的主页置顶或专栏收录,并制作了电子书供大家参考,有需要的小伙伴可以关注私信我,因为属于技术散文风格…...
为什么选择在Facebook投放广告?
2024年了你还没对 Facebook 广告产生兴趣?那你可就亏大了! 今天这篇文章,我们会分享它对你扩大业务的好处。要知道,Facebook 广告凭借它庞大的用户群和先进的定位选项,已经是企业主们有效接触目标受众的必备神器。接下…...
10 ARM 体系
10 ARM 体系 ARM体系1、基本概念1.1 常见的处理器1.2 ARM7三级指令流水线1.3 初识PC寄存器 2、 ARM核的七种工作模式3、ARM核七种异常 ARM体系 1、基本概念 1.1 常见的处理器 PowerPC处理器:飞思卡尔MPC系列 DSP:TI达芬奇系列 FPGA:Xilinx赛灵思的ZYN…...
指令)
ubuntu中设置开机自动运行的(sudo)指令
ubuntu版本:22.04.4 在Ubuntu中设置开机自动运行某一条(需要sudo权限的)指令,我们可以通过编辑系统的启动脚本来实现: 创建一个新的启动脚本:创建一个新的脚本文件,并将其放置在 /etc/init.d/ 目…...

删掉Elasticsearch6.x 的 .security-6索引会怎么样?
背景 玩了下 Elasticsearch 的认证,启动 ES 并添加认证后,看到索引列表额外多了一个 .security-6 。以为是没用的,手欠就给删掉了,然后 Elasticsearch 就访问不了了。 只好再重新部署,再看索引内容,发现这…...
Navicat Premium15 下载与安装(免费版)以及链接SqlServer数据库
转自:https://blog.csdn.net/m0_75188141/article/details/139842565...
Vue3配置vite.config.js代理解决跨域问题
前言: 当浏览器发出一个请求时,只要请求URL的协议、域名、端口三者之间任意一个与当前页面URL不同,就称为跨域。 跨域一般出现在开发阶段,由于线上环境前端代码被打包成了静态资源,因而不会出现跨域问题,这篇文章主要给大家介绍了关于Vue3配置vite.config.js解决跨域问题的相…...

Solidity面试题,由浅入深
Solidity是Ethereum智能合约的主要编程语言,面试题的设计旨在评估候选人对Solidity语言特性的掌握程度,以及他们对区块链和智能合约的理解。下面列出了一些常见的Solidity面试题,涵盖基础知识到高级概念,并简要说明每个问题的答案…...
变量的注意或许需要调试
输入一个自然数N(1<N<9),从小到大输出用1~N组成的所有排列,也就说全排列。例如输入3则输出 123 132 213 231 312 321 输入格式: 输入一个自然数N(1<N<9) 输出格式: N的全排列,每行一…...

C# 增删改查教程 代码超级简单
目录 一.留言 二 .帮助类 三 .增删改查代码展示 一.留言 大家好,前几篇文章我们更新了 C# 三层架构的相关代码,主要写了登录,以及增删改查的相关代码,用的三层架构的框架,那么本篇文章一次性更新C#的增删改查相关代…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...
