数据结构之栈的使用
栈是计算机科学中一个重要的数据结构。它是一种特殊的线性表,只允许在一端进行进出操作。这一端被称为栈顶,另外一端被称为栈底。栈的特点是后进先出,即最后进入栈的元素会先被弹出栈。栈的应用广泛,例如在编译器中,栈被用来实现表达式的求值和函数的调用。在操作系统中,栈被用来处理函数调用、异常处理和内存分配等。
栈的基本操作有两个:入栈和出栈。在入栈操作中,元素首先被压入栈顶,并将栈顶指针向上移动一位。在出栈操作中,元素从栈顶弹出,并将栈顶指针向下移动一位。当栈为空时,栈顶指针指向栈底。
栈可以用数组或链表来实现。使用数组实现的栈被称为顺序栈,使用链表实现的栈被称为链式栈。顺序栈的优点是随机访问速度快,但是缺点是容量固定,当栈满时无法再进行入栈操作。链式栈的容量可以动态增长,但是访问速度相对较慢。
常见的栈的应用场景包括函数调用、表达式求值、括号匹配等。在函数调用中,每进入一个函数,就将返回地址和一些参数压入栈中,当函数返回时,再从栈中弹出这些值。在表达式求值中,使用两个栈来分别存储操作数和操作符,通过比较操作符的优先级来进行计算。在括号匹配中,每遇到一个左括号就将其压入栈中,当遇到右括号时,弹出栈顶元素进行匹配。如果最终栈为空,则表示所有的括号都匹配成功。
由于栈的特殊性质和广泛应用,学习栈成为计算机科学中重要的知识点之一。在实际编程中,熟练掌握栈的相关操作和应用,有助于增强程序设计的能力。同时,栈的实现也是许多其他数据结构和算法的基础,例如队列、图的深度优先搜索等,因此深入了解栈的原理和实现对于进一步学习计算机科学非常有帮助。
在使用栈时,需要注意栈的溢出和下溢问题。栈的溢出指在入栈操作时,栈已经满了,无法再继续入栈,这时应该进行相应的处理,例如扩容操作;栈的下溢指在出栈操作时,栈已经为空,无法继续出栈,这时也需要进行相应的处理,例如抛出异常或者返回默认值。
栈作为一种重要的数据结构,在各种应用场景中发挥着重要的作用。通过深入了解栈的实现和应用,可以提高程序设计的效率和质量,也有助于理解其他数据结构和算法的原理和实现。同时,在使用栈时需要注意栈的溢出和下溢问题,这样才能保证程序的稳定性和可靠性。
栈(Stack)是一种基于先进后出(LIFO)原则的数据结构,它可以用数组或链表实现。栈限定了只能在表尾进行插入和删除操作。
下面是一个用数组实现的栈的代码示例:
```
#include <iostream>
using namespace std;
const int MAXSIZE = 100; // 定义栈的最大容量
class Stack {
private:
int top; // 栈顶指针
int data[MAXSIZE]; // 栈元素数组
public:
Stack() { top = -1; } // 构造函数,初始化 top 为 -1
bool push(int x);
int pop();
bool isEmpty();
};
/* 插入元素 x 到栈顶 */
bool Stack::push(int x) {
if (top >= MAXSIZE - 1) { // 栈已满
cout << "Stack overflow." << endl;
return false;
}
data[++top] = x; // 将 x 插入栈顶,并将 top 加一
return true;
}
/* 弹出栈顶元素 */
int Stack::pop() {
if (isEmpty()) { // 栈为空
cout << "Stack underflow." << endl;
return -1;
}
return data[top--]; // 返回栈顶元素,并将 top 指针减一
}
/* 判断栈是否为空 */
bool Stack::isEmpty() {
return (top == -1);
}
int main() {
Stack s;
s.push(1);
s.push(2);
s.push(3);
cout << s.pop() << endl; // 输出 3
cout << s.pop() << endl; // 输出 2
cout << s.pop() << endl; // 输出 1
cout << s.pop() << endl; // 输出 "Stack underflow."
return 0;
}
```
以上代码中,栈的核心操作包括:
- `push`:将元素插入栈顶。
- `pop`:弹出栈顶元素。
- `isEmpty`:判断栈是否为空。
在使用栈时要注意栈的容量限制,避免栈溢出。另外,插入和删除操作的时间复杂度为 O(1)。
总的来说,栈可用于许多场景,如括号匹配、计算表达式等,这些应用需要对栈的性质有深入理解,并熟练掌握栈相关的算法和操作。
相关文章:

数据结构之栈的使用
栈是计算机科学中一个重要的数据结构。它是一种特殊的线性表,只允许在一端进行进出操作。这一端被称为栈顶,另外一端被称为栈底。栈的特点是后进先出,即最后进入栈的元素会先被弹出栈。栈的应用广泛,例如在编译器中,栈…...
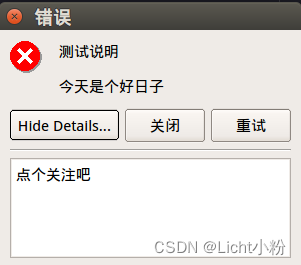
QMessageBox手动添加按钮并绑定按钮的信号
视频展示效果(结合代码看效果更佳哦,代码在最下面): QMessageBox手动添加有重试效果的按钮效果图: 点击详细文本之后展开如下图: 图标可选: QMessageBox::Critical错误图标QMessageBox::NoIco…...
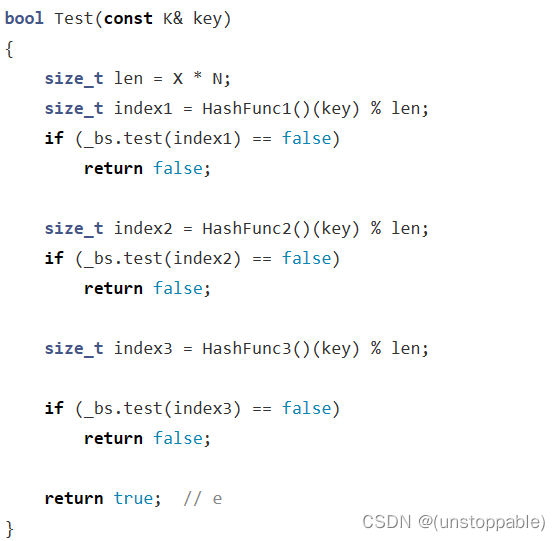
【C++进阶】位图和布隆过滤器
文章目录位图位图概念位图使用场景位图的结构构造setresettest完整代码布隆过滤器布隆过滤器概念布隆过滤器结构构造setresettest完整版代码位图 位图概念 所谓位图,就是用每一位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用…...
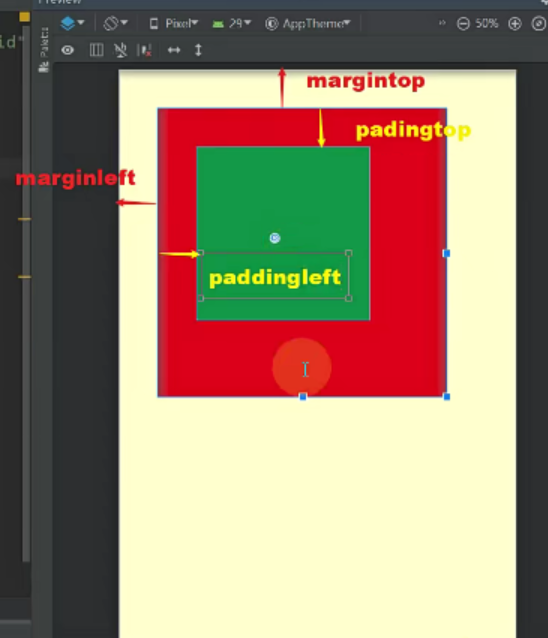
Android开发-Android UI与布局
01 Android UI 1.1 UI 用户界面(User Interface,简称 UI,亦称使用者界面)是系统和用户之间进行交互和信息交换的媒介,它实现信息的内部形式与人类可以接受形式之间的转换。软件设计可分为两个部分:编码设计与UI设计。 1.2 Andr…...
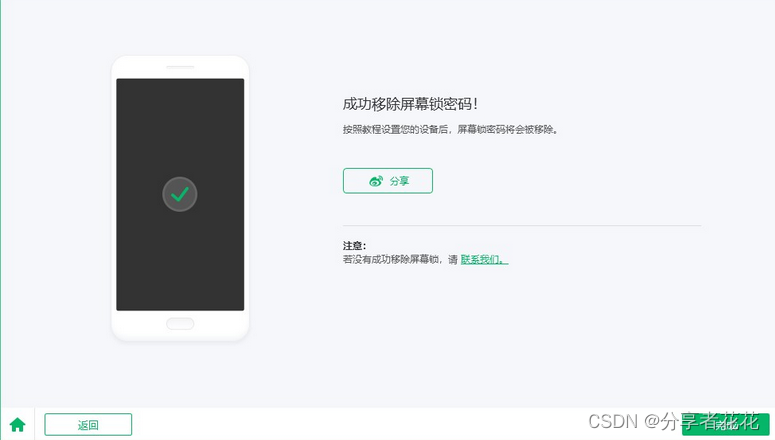
在不丢失数据的情况下解锁锁定的 Android 手机的 4 种方法
尽管您可以使用指纹解锁手机,但大多数智能手机都需要 PIN 码、图案或字母数字代码作为主密码。如果您有一段时间没有输入手机密码,很容易忘记。正是由于这个原因,即使您打开了指纹解锁,大多数智能手机也会让您每天至少输入一次 PI…...

【11】核心易中期刊推荐——人工智能 | 图形图像处理
🚀🚀🚀NEW!!!核心易中期刊推荐栏目来啦 ~ 📚🍀 核心期刊在国内的应用范围非常广,核心期刊发表论文是国内很多作者晋升的硬性要求,并且在国内属于顶尖论文发表,具有很高的学术价值。在中文核心目录体系中,权威代表有CSSCI、CSCD和北大核心。其中,中文期刊的数…...

Spring 中的事件发布与监听
主要代码在org.springframework.context,org.springframework.context.event包中 事件发布与监听主要包含以下角色: 事件:ApplicationEvent事件监听器:ApplicationListener SmartApplicationListener GenericApplicationListene…...

c++ 一些常识 2
前言 今天主要讲类相关概念。 构造和析构函数是否可以抛出异常 在构造函数中抛出异常,控制权会转出构造函数之外,对象的析构函数不会被调用,造成内存泄漏。 如果析构函数中抛出异常,而且没有在当地捕捉,析构函数便执…...
用嘴写代码?继ChatGPT和NewBing之后,微软又开始整活了,Github Copilot X!
用嘴写代码?继ChatGPT和NewBing之后,微软又开始整活了,Github Copilot X! AI盛行的时代来临了,在这段时间,除了爆火的GPT3.5后,OpenAI发布了GPT4版本,同时微软也在Bing上开始加入了A…...

3分钟阐述这些年我的 接口自动化测试 职业生涯经验分享
接口自动化测试学习教程地址:https://www.bilibili.com/video/BV1914y1F7Bv/ 你好,我是凡哥。 很高兴能够分享我的接口自动化测试经验和心得体会。在我目前的职业生涯中,接口自动化测试是我经常进行的一项任务。通过不断地学习和实践…...

十大Python可视化工具,太强了
今天介绍Python当中十大可视化工具,每一个都独具特色,惊艳一方。 Matplotlib Matplotlib 是 Python 的一个绘图库,可以绘制出高质量的折线图、散点图、柱状图、条形图等等。它也是许多其他可视化库的基础。 import matplotlib.pyplot as p…...

五.ElasticSearch的基础+实战
五.ElasticSearch的基础+实战 1.Elasticsearch的是什么? 2.Elasticsearch的作用是什么? 3.Elasticsearch的核心思想? 4.Elasticsearch启动与简单使用 5.kibana结合elasticsearch实现简单的增删改查 6.elasticsearch安装中文分词器 7.elasticsearch结合springboot开发…...

Oracle的学习心得和知识总结(十三)|Oracle数据库Real Application Testing之Database Reply实操(一)
目录结构 注:提前言明 本文借鉴了以下博主、书籍或网站的内容,其列表如下: 1、参考书籍:《Oracle Database SQL Language Reference》 2、参考书籍:《PostgreSQL中文手册》 3、EDB Postgres Advanced Server User Guid…...

CAD外部参照如何重新定位?CAD外部参照重定位步骤
CAD外部参照如何重新定位?这个问题并不算是一个常见的问题,但偶尔也会遇到,今天小编就来给大家简单介绍一下浩辰CAD软件中CAD外部参照重定位的操作步骤,一起来看看吧! CAD外部参照重定位步骤: 浩辰CAD软件…...

11. C#高级进阶
一、C# 异常处理 在 C# 中,异常是在程序运行出错时引发的,所有异常都派生自 System.Exception 类。异常处理就是处理运行时错误的过程,通过异常处理可以使程序在发生错误时保持正常运行。 C# 中的异常处理基于四个关键字构建,分别…...
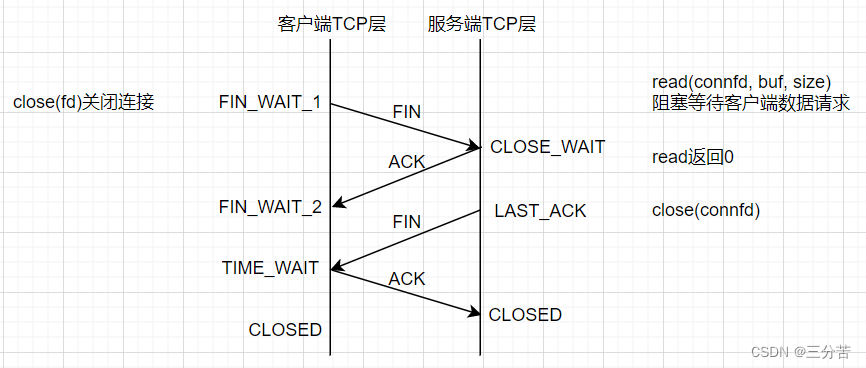
网络编程套接字( TCP协议通讯流程)
目录 1、绑定失败问题 2、TCP协议通讯流程 三次握手的过程 数据传输的过程 四次挥手的过程 TCP和UDP对比 1、绑定失败问题 当我们测试网络代码时,先将服务端绑定8080端口运行,然后运行客户端,并让客户端连接当前服务器: 当有客户…...

WPF毛笔字实现过程
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
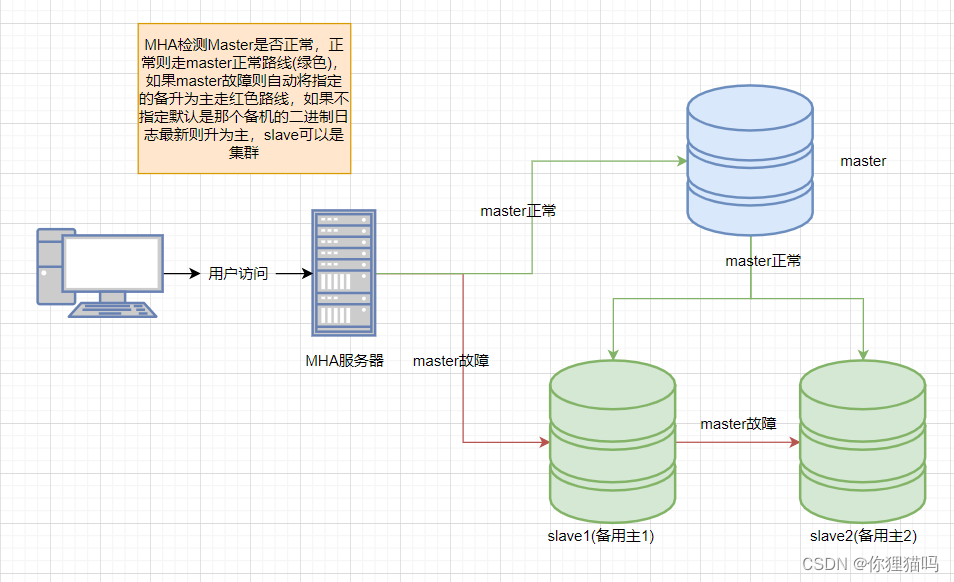
MHA实现mysql数据库高可用
目录 MHA原理 MHA工具包 MHA实现mysql高可用实战 MHA原理 ①MHA利用 SELECT 1 As Value 指令判断master服务器的健康性,一旦master 宕机,MHA 从宕机崩溃的master保存二进制日志事件(binlog events) ②识别含有最新更新的slave ③应用差异的中继日志&…...

leetcode每日一题:55. 跳跃游戏
系列:贪心算法 语言:java 题目来源:Leetcode55. 跳跃游戏 题目 给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。 数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标。 示例 1: 输…...

【C++】map 和 set
文章目录一、关联式容器与键值对1、关联式容器2、键值对 pair3、树形结构的关联式容器二、set1、set 的介绍2、set 的使用三、multiset四、map1、map 的介绍2、map 的使用五、multimap一、关联式容器与键值对 1、关联式容器 在C初阶的时候,我们已经接触了 STL 中的…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
