排序算法详解
💎所属专栏:数据结构与算法学习
💎 欢迎大家互三:2的n次方_

🍁1. 插入排序
🍁1.1 直接插入排序
插入排序是一种简单直观的排序算法,它的原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
以从小到大排序为例
1.从第一个元素开始,可以看作是有序的元素
2.取出下一个元素,与前面已经排好序的元素比较,如果前面的元素大于此元素,就把前面的元素往后移,继续往前找,找到小于或等于的位置进行插入,直到找到最前面

public class InsertSort {public static void main(String[] args) {int[] arr = {5, 1, 2, 4, 3};insertSort(arr);System.out.println(Arrays.toString(arr));}public static void insertSort(int[] arr) {for (int i = 1; i < arr.length; i++) {int tmp = arr[i];int j = i - 1;//比tmp大的元素往后移for (; j >= 0 && arr[j] > tmp; j--) {arr[j + 1] = arr[j];}arr[j + 1] = tmp;}}
}🍁1.2 希尔排序
希尔排序的基本思想是:
先选定一个整数,把待排序的数据分为多个组,对每一个组内进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。

假设有一个数组
arr = [9, 8, 3, 7, 5, 6, 4, 1],我们采用最简单的增量序列(每次减半)来进行希尔排序:1. 初始增量
d = 4,将数组分为4组,每组进行插入排序:[9, 7], [8, 5], [3, 6], [4, 1]2. 增量
d = 2,将数组分为2组,每组进行插入排序:[7, 5, 6, 1], [9, 8, 3, 4]3. 增量
d = 1,整个数组作为一组进行插入排序,得到最终结果:[1, 3, 4, 5, 6, 7, 8, 9]
public static void shellSort(int[] arr) {int gap = arr.length;//增量每次减半while (gap > 1) {gap /= 2;shell(arr, gap);}}private static void shell(int[] arr, int gap) {for (int i = gap; i < arr.length; i++) {int tmp = arr[i];int j = i - gap;//比tmp大的元素往后移for (; j >= 0 && arr[j] > tmp; j -= gap) {arr[j + gap] = arr[j];}arr[j + gap] = tmp;}}🍁2. 选择排序
🍁2.1 直接选择排序
直接选择排序的思想:
每次从待排序的数据中选择一个最小(最大)的元素放在序列起始位置,直到整个序列元素排序完毕

public static void selectSort(int[] arr) {for (int i = 0; i < arr.length; i++) {int minIndex = i;for (int j = i + 1; j < arr.length; j++) {if (arr[j] < arr[minIndex]) {minIndex = j;}}swap(arr, i, minIndex);}}🍁2.2 堆排序
堆排序在上一节中已经有过介绍,这里再简单回顾下,还是以从小到大排序为例,这时我们创建一个大根堆,堆顶元素也就是最大的,把最顶元素和堆尾元素进行交换,接着向下调整,再把堆顶元素和堆尾元素进行交换,也就是排在了上一个最大元素的前面,重复此过程,就实现了从小到大排序。
上一篇回顾
public static void heapSort(int[] arr) {createHeap(arr);int end = arr.length - 1;while (end > 0) {//堆顶和end元素互换swap(arr, 0, end);//向下调整siftDown(arr, 0, end);end--;}}public static void createHeap(int[] arr) {for (int parent = (arr.length - 1 - 1) / 2; parent >= 0; parent--) {siftDown(arr, parent, arr.length);}}private static void siftDown(int[] arr, int parent, int length) {int child = 2 * parent + 1;while (child < length) {if (child + 1 < length && arr[child] < arr[child + 1]) {child += 1;}if (arr[child] > arr[parent]) {swap(arr, child, parent);child = 2 * child + 1;} else {break;}}}
🍁3. 交换排序
🍁3.1 冒泡排序
冒泡排序是一种简单的排序算法,它重复地遍历要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。
比较每一对相邻的元素:如果第一个比第二个大(升序排序),就交换它们两个,这步做完后,最后的元素会是最大的数。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。

public static void bubbleSort(int[] arr) {for (int i = 0; i < arr.length - 1; i++) {boolean flag = false;for (int j = 0; j < arr.length - 1 - i; j++) {if (arr[j] > arr[j + 1]) {swap(arr, j, j + 1);flag = true;}}//如果这一趟没有交换任何一对元素,表示已经排好序了if(!flag){break;}}}这里做了一个优化,如果给出的数据只有一对数据不符合顺序,那么交换这对数据之后就不用再重复后续的程序了,所以直接结束循环即可,在一些情况下,通过这种优化,冒泡排序的时间复杂度可以达到O(n)
🍁3.2 快速排序
首先把0索引的位置当作基准数,定义两个指针,先将右指针从数组末尾开始往前找,遇到比基准数小的停下来,左指针从1索引开始往后找,遇到比基准数大的停下来,交换左右指针的数,重复此过程,直到左右指针相遇,此时和基准数交换,就可以把基准数排到正确的位置,此时左边都是比基准数小的,右边都是比基准数大的,再依次递归基准数左边部分和右边部分,就实现了排序
注意:一定要先从右边开始找比基准数小的,先从左边开始就无法达到效果

public static void quickSort(int[] arr, int start, int end) {if (start >= end) {return;}int mid = part(arr, start, end);quickSort(arr, start, mid - 1);quickSort(arr, mid + 1, end);}public static int part(int[] arr, int i, int j) {int tmp = arr[i];int tmpStart = i;while (i < j) {while (i < j && arr[j] >= tmp) {j--;}while (i < j && arr[i] <= tmp) {i++;}swap(arr, i, j);}swap(arr, tmpStart, i);return i;}关于基准数归位的过程还有一种优化的方法,由于上面使用了大量的交换,也会浪费一些时间
public static int part1(int[] arr, int i, int j) {int tmp = arr[i];while (i < j) {while (i < j && arr[j] >= tmp) {j--;}arr[i] = arr[j];while (i < j && arr[i] <= tmp) {i++;}arr[j] = arr[i];}arr[i] = tmp;return i;}也就是先把基准数拿出来,这时就留出来一个空位,接着从右边找比基准数小的,填上空位,再从左边找比基准数大的,再填上右边的空位,以此类推
还有一个优化的点是,输入数组已经是有序(升序或降序)的,或者每次划分(partition)操作都选择到最小(或最大)的元素作为基准(pivot),导致每次划分只将一个元素移到它最终的位置上,而其他所有元素都留在原数组的另一侧。这种情况下,每次划分后的递归调用处理的子数组大小几乎相同,递归的深度接近n,导致总的比较和交换次数接近n^2。
下面通过三数取中法来更换基准数进行优化
private static int getMid(int[] arr, int left, int right) {int mid = (left + right) / 2;if (arr[left] > arr[right]) {if (arr[mid] > arr[left]) {return left;} else if (arr[mid] < arr[right]) {return right;} else {return mid;}} else {if (arr[mid] > arr[right]) {return right;} else if (arr[mid] < arr[left]) {return left;} else {return mid;}}}获取中位数之后进行交换:

另一个可以优化的是,由于快速排序的递归是一棵二叉树,每一层都是指数级的增长,所以最后两层会有很多递归需要走,但此时元素也趋于有序,就可以调用插入排序
if(end - start + 1 <= 3){insertSort(arr,start,end);return;}非递归实现
递归需要一直在栈上开辟空间,容易造成栈溢出,这里我们直接通过栈来进行非递归的实现
public static void yquickSort(int[] arr,int start,int end){Stack<Integer> stack = new Stack<>();int pivot = part1(arr,start,end);if(pivot > start + 1){stack.push(start);stack.push(pivot - 1);}if(pivot < end - 1){stack.push(pivot + 1);stack.push(end);}while(!stack.isEmpty()){end = stack.pop();start = stack.pop();pivot = part1(arr,start,end);if(pivot > start + 1){stack.push(start);stack.push(pivot - 1);}if(pivot < end - 1){stack.push(pivot + 1);stack.push(end);}}}🍁4. 归并排序
归并排序主要利用了分治法,先使每个子序列有序,再使子序列段间有序,组后合并分解的子序列

首先把要排序的数组依次分解,直到两两一组,之后开始合并,合并的过程也就是把两个有序数组再合并为一个有序数组的过程,每次取出两个数组的较小者存入合并的数组中,最终合并为一整个数组
public static void mergeSort(int[] arr, int left, int right) {if (left >= right) return;int mid = (left + right) / 2;mergeSort(arr, left, mid);mergeSort(arr, mid + 1, right);merge(arr, left, mid, right);}//也就是合并两个有序数组public static void merge(int[] arr, int left, int mid, int right) {int[] tmp = new int[right - left + 1];int k = 0;int s1 = left;int s2 = mid + 1;//将分解后的两个数组每次取出最小值放在tmp数组中while (s1 <= mid && s2 <= right) {if (arr[s1] >= arr[s2]) {tmp[k++] = arr[s2++];} else {tmp[k++] = arr[s1++];}}while (s1 <= mid) {tmp[k++] = arr[s1++];}while (s2 <= right) {tmp[k++] = arr[s2++];}for (int i = 0; i < k; i++) {arr[left + i] = tmp[i];}}非递归实现归并排序
非递归实现也就是通过循环来模拟递归,依次合并数组,gap取
public static void mergeSortNor(int[] arr) {int gap = 1;while (gap < arr.length) {for (int i = 0; i < arr.length; i += gap * 2) {int left = i;int mid = i + gap - 1;if (mid >= arr.length) {mid = arr.length - 1;}int right = mid + gap;if (right >= arr.length) {right = arr.length - 1;}merge(arr, left, mid, right);}gap *= 2;}}🍁5. 计数排序
计数排序是一种基于非比较的排序算法,计数排序的主要特点是通过统计每个元素出现的次数,来确定每个元素在排序后数组中的位置,从而实现排序。

计算出以上数据出现的次数之后,再根据次数进行遍历,就可以达到排序的效果
public static void countSort(int[] arr) {int maxVal = arr[0];int minVal = arr[0];//找到最大值和最小值for (int i = 0; i < arr.length; i++) {if (arr[i] > maxVal) {maxVal = arr[i];}if (arr[i] < minVal) {minVal = arr[i];}}int[] tmp = new int[maxVal - minVal + 1];//开始计数for (int i = 0; i < arr.length; i++) {tmp[arr[i] - minVal]++;}int index = 0;//将数据赋值给数组for (int i = 0; i < tmp.length; i++) {while (tmp[i]-- != 0) {arr[index] = i + minVal;index++;}}}
相关文章:

排序算法详解
💎所属专栏:数据结构与算法学习 💎 欢迎大家互三:2的n次方_ 🍁1. 插入排序 🍁1.1 直接插入排序 插入排序是一种简单直观的排序算法,它的原理是通过构建有序序列,对于未排序数…...
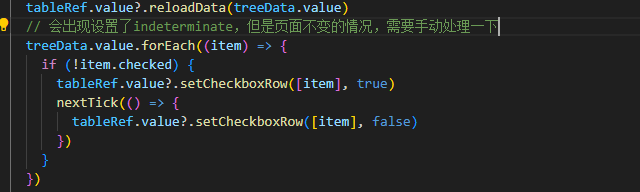
vxe-table树形结构使用setCheckboxRow卡顿--已解决
项目场景: vxe-table树形结构使用setCheckboxRow进行部分节点选中 问题描述 vxe-table树形结构使用setCheckboxRow,在数据较多时卡顿 原因分析: setCheckboxRow内部进行了多次的循环遍历,导致速度慢 解决方案: 设…...

配置错误和 IAM 弱点是云安全的主要隐患
根据云安全联盟发布的《2024 年云计算最大威胁》报告,通常与云服务提供商 (CSP) 相关的传统云安全问题的重要性正在持续下降。 配置错误、IAM 弱点和 API 风险仍然至关重要 这些发现延续了 2022 年报告中首次发现的轨迹,同时,诸如错误配置的…...

Redis系列之Redis Cluster
概述 Redis 2.8版本发布稳定版Redis Sentinel,不过Sentinel集群版存在一些问题: 高可用性:Sentinel集群对Redis既有的主从集群提供有限的高可用保障;在线扩容:节点下线,触发选举,选举涉及两个…...

网站证书过期导致WordPress后台无法登录问题解决,页面样式丢失
1、首先打开网站目录文件\wp-includes\functions.php,找到代码,应该就是就在在第8行。 require( ABSPATH . WPINC . /option.php ); 在下面添加以下代码,作用就是把http替换为https add_filter(script_loader_src, agnostic_script_loader…...

LeetCode刷题笔记第191题:位1的个数
LeetCode刷题笔记第191题:位1的个数 题目: 想法: 通过位运算判断二级制形式中有多少个1,代码及解释如下: class Solution:def hammingWeight(self, n: int) -> int:return sum(1 for i in range(32) if n & …...
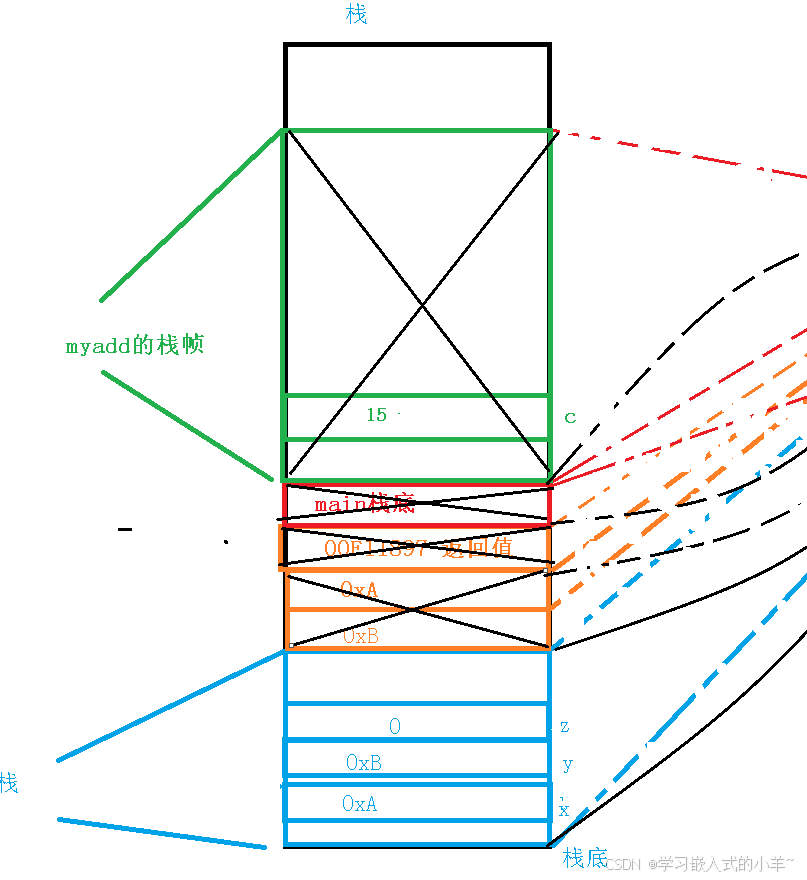
C语言—函数栈帧
函数,一般都有返回值,函数名,参数,再下来还有什么mian函数,函数写出来就是要被调用的,上面图片上的代码,main函数和myadd函数,都要在自己的栈结构什么形成自己的栈,可以帮…...
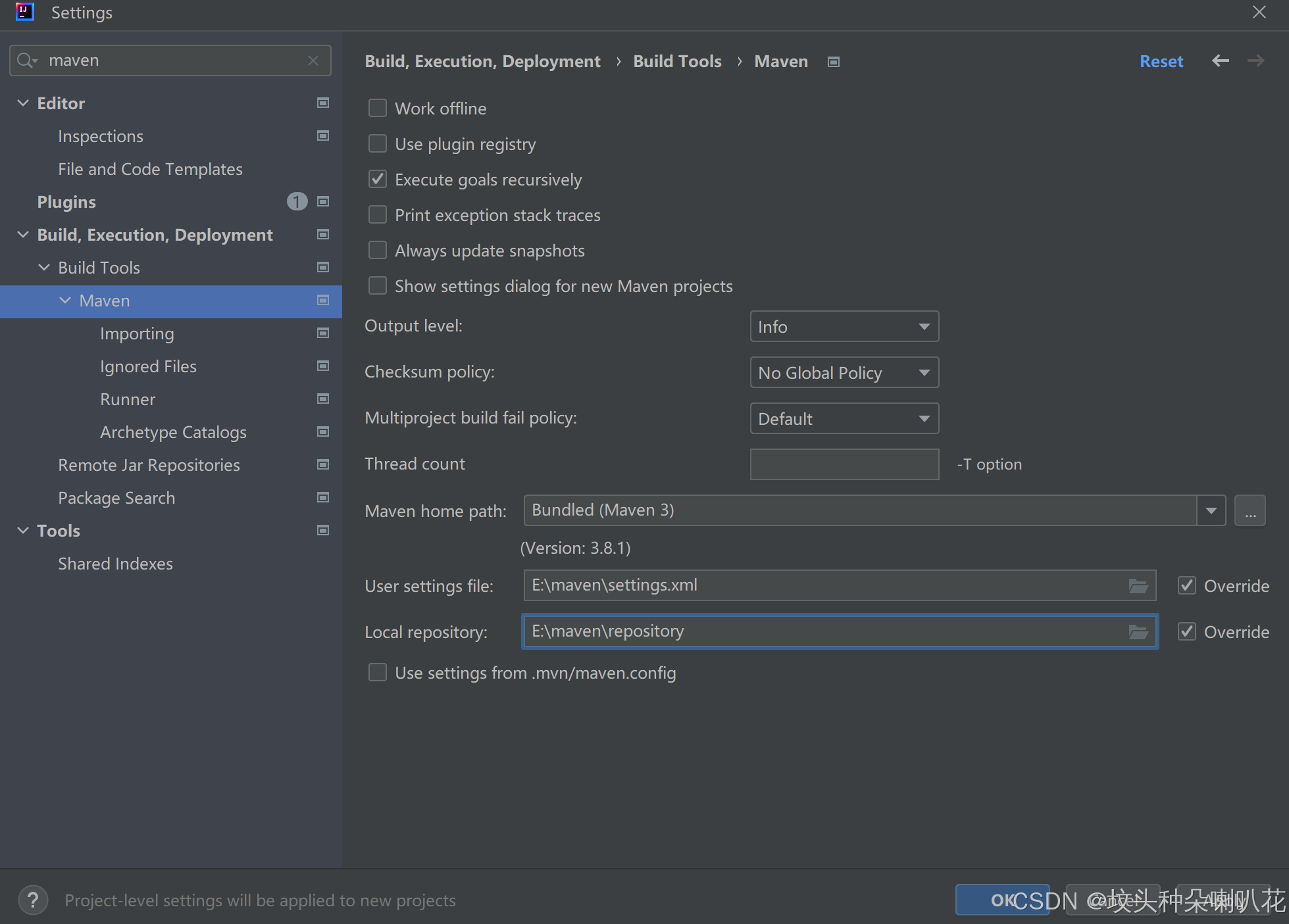
IDEA 2022.1.4用前需知
目录 一、配置国内源 二、正确再次创建新项目方式 IDEA 2022.1.4下载地址 一、配置国内源 1、查看本地仓库地址 2、设置国内源-添加Setting.xml文件内容 3、修改目录(考虑到当前硬盘空间大小,英文目录名) 1)创建你要移动过去…...
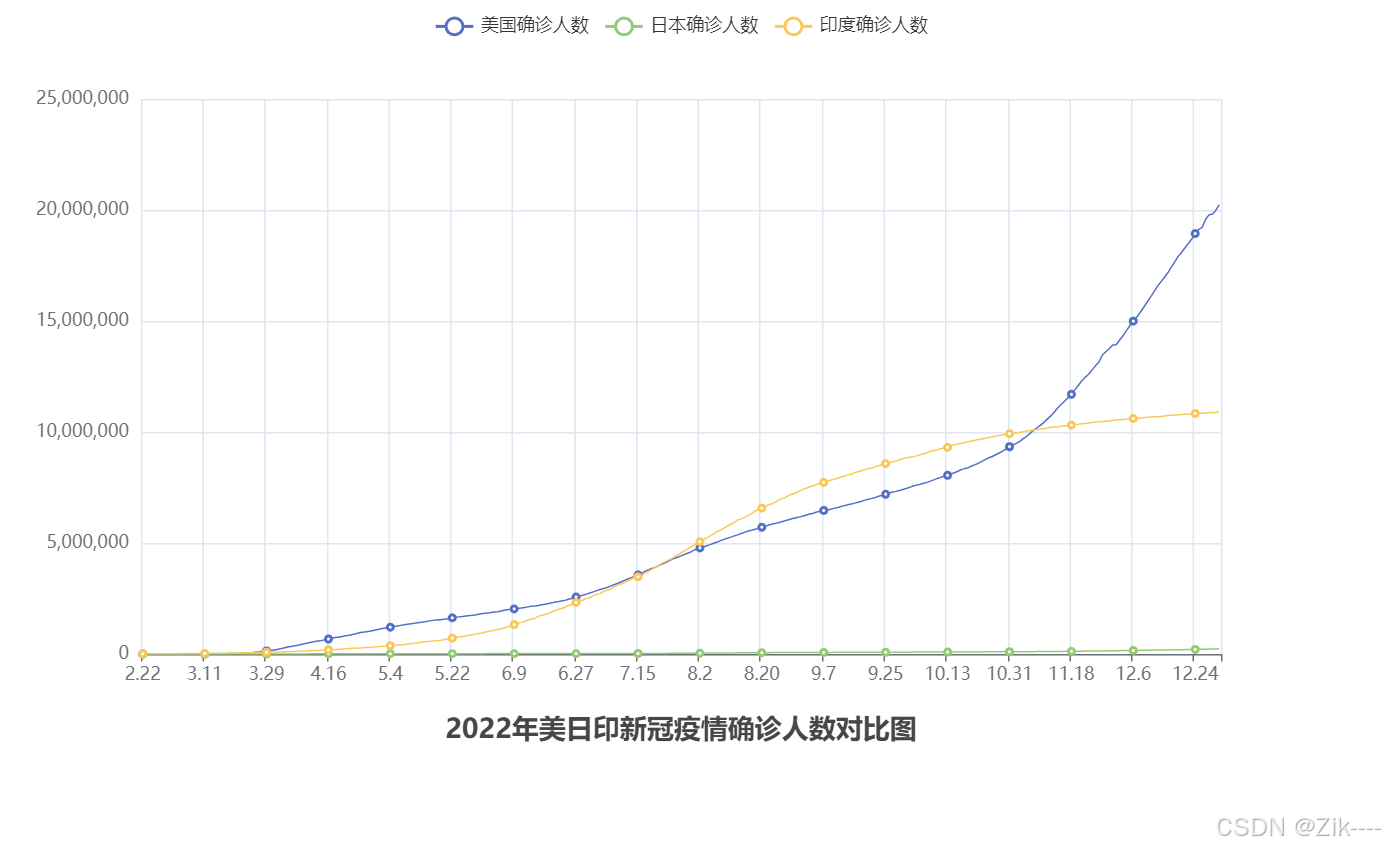
Python数据可视化案例——折线图
目录 json介绍: Pyecharts介绍 安装pyecharts包 构建一个基础的折线图 配置全局配置项 综合案例: 使用工具对数据进行查看 : 数据处理 json介绍: json是一种轻量级的数据交互格式,采用完全独立于编程语言的文…...
Ubuntu虚拟机安装及汉化
一、安装 1.勾选典型(推荐)(T)——点击下一步 2.点击浏览找到光盘映像文件打开(此文件很重要安装好后安装包不要卸载,放在不容易被删除的地方)——点击下一步 3.将信息补充完整——点击下一步 4.点击浏览选择要将虚拟机安装在哪个路径&…...
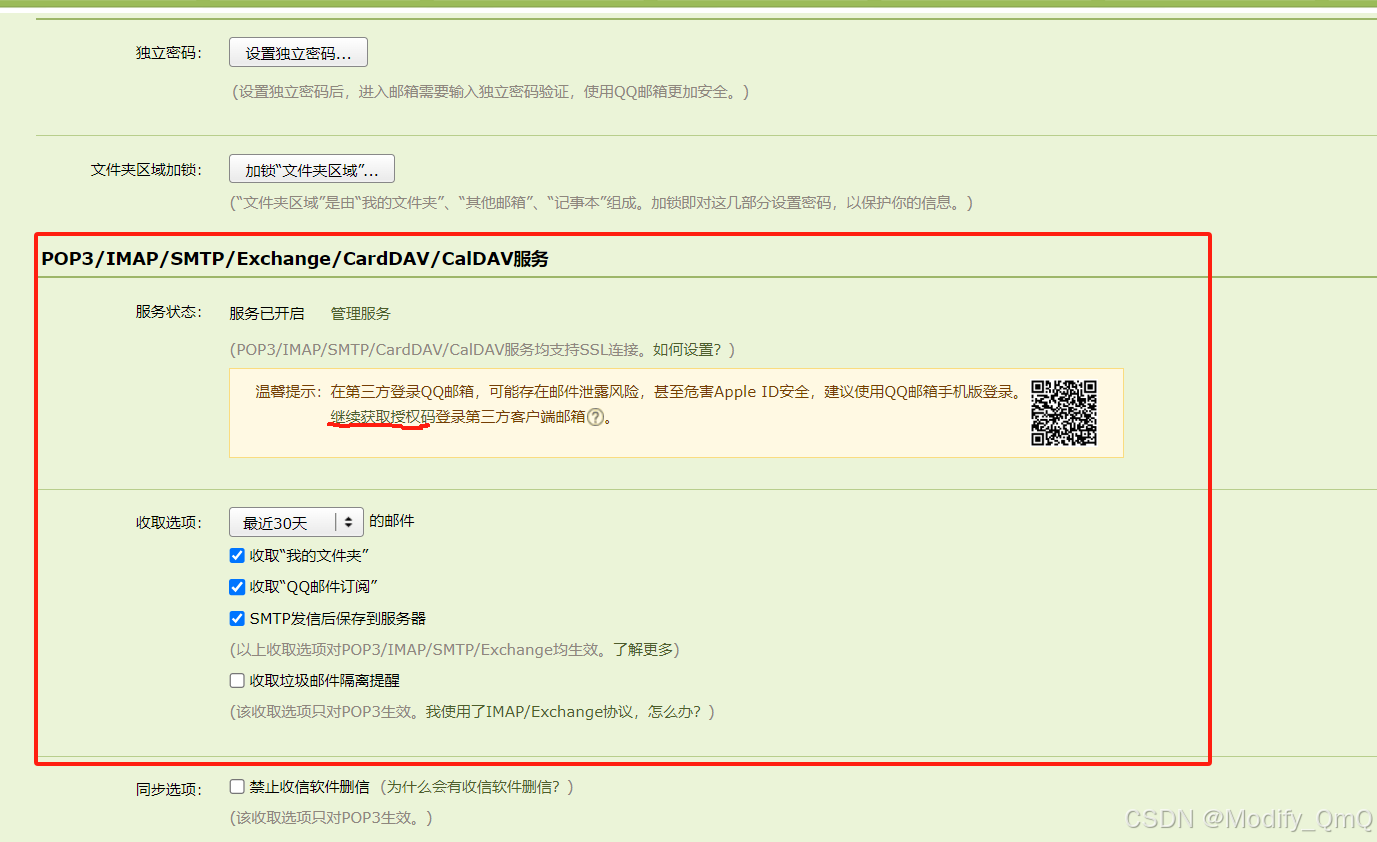
记2024-08原生微信小程序开发
继2024.08 最近需要开发一个微信小程序的一个功能模块,但是之前在学的时候都是好几年前的东东了,然后重新快速过了一遍b站大学的教程,这篇文章就是基于教程进行的一些总结,和自己开发过程当中使用到的一些点和一些技巧什么的吧。 …...

嵌入式linux系统镜像制作day1
点击上方"蓝字"关注我们 01、前言 嵌入式设备(例如心电图检测仪,售票系统等)。尽管,嵌入式设备像那些智能手机一样,绝大多数都使用同样的硬件和软件,包括系统芯片SoC、储存、连接和多媒体接口、…...

【相机与图像】2. 相机内外参的标定的代码示例
1 摄像头内参的标定 【相机标定具体操作】 使用将要标定的摄像头,以不同的角度采集棋盘格,要保证视野内出现完整的棋盘格。采集图片数量约15张左右即可。 以11*8的棋盘格为例,具体流程如下: step 1. 设置棋盘格3D点;通…...

重启人生计划-拒绝内耗
🥳🥳🥳 茫茫人海千千万万,感谢这一刻你看到了我的文章,感谢观赏,大家好呀,我是最爱吃鱼罐头,大家可以叫鱼罐头呦~🥳🥳🥳 如果你觉得这个【重启人生…...

盘点电脑开机慢的几大高频原因
常规的话一台电脑正常我们都要用个2年以上的时间,有的可能更长,5年的都有,而电脑目前占多数的主流操作系统就是微软的Windows。那么随着使用年限的增加,无论是系统还是电脑硬件,都会随着使用次数和使用的时间的增加而有损耗,系统软件上就是文件越来越臃肿,空间越来越小,…...
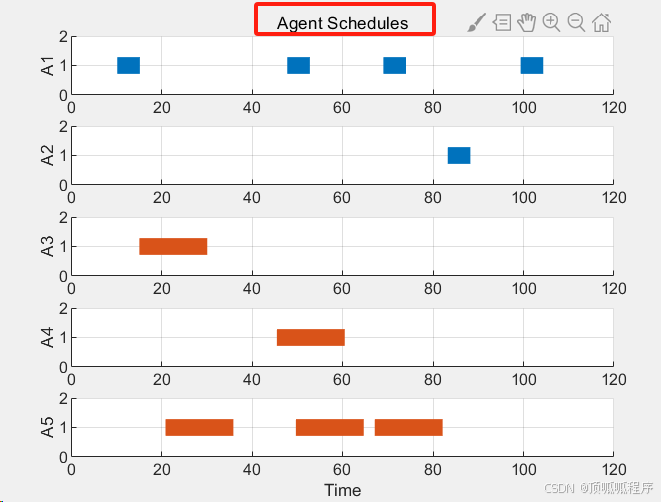
2-64 基于matlab的Consensus-Based Bundle Algorithm (CBBA)算法
基于matlab的Consensus-Based Bundle Algorithm (CBBA)算法,可为异构代理网络上的多代理多任务分配问题提供良好的解决方案。支持具有有效时间窗口的任务、异构代理-任务兼容性要求,以及平衡任务奖励和燃料成本的得分函数。奖励和燃料成本的分数函数。程…...

Win10 去掉桌面右上角 了解有关此图片的信息
1. 进入注册表 Win R运行regedit 2. 找到以下路径 计算机\HKEY_CURRENT_USER\SOFTWARE\Microsoft\Windows\CurrentVersion\Explorer\HideDesktopIcons\NewStartPanel 3. 新建 DWORD(32位)值(D) 右击 NewStartPanel新建 DWORD…...

tcpdump入门——抓取三次握手数据包
1. 使用docker启动一个tcp应用 参考:https://blog.csdn.net/LONG_Yi_1994/article/details/141175526 2. 获取容器id docker ps |grep gochat 3. 获取容器的 PID 首先,你需要获得容器的进程 ID(PID)。可以使用 docker inspect…...

漏洞复现-GitLab任意读取文件(CVE-2023-2825)
1.漏洞描述 GitLab是一个用于仓库管理系统的开源项目,其使用Git作为代码管理工具,可通过Web界面访问公开或私人项目。据悉,该漏洞影响 GitLab社区版(CE)和企业版(EE)的 16.0.0 版本,其它更早的版本几乎都不受影响。 该漏洞存在于GitLab CE/EE版本16.0.0…...

二叉树——9.找树左下角的值
力扣题目链接 给定一个二叉树,在树的最后一行找到最左边的值。 示例: 输出:7 题干很简单,找到树的最后一行,在该行找到最左边的值,结合完整代码进行分析。 完整代码如下: class Solution:d…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
