二分查找——我欲修仙(功法篇)
个人主页:【😊个人主页】
系列专栏:【❤️我欲修仙】
学习名言:临渊羡鱼,不如退而结网——《汉书董仲舒传》
系列文章目录
第一章 ❤️ 二分查找
文章目录
- 系列文章目录
- 前言🚗🚗🚗
- 二分查找?
- 第一阶段 二分查找?🤔🤔🤔
- 第二阶段 易错点😬😬😬
- 问题一:
- 问题二
- 总结
- 题目代码(C语言实现)
前言🚗🚗🚗
经历了一段时间的《数据结构与算法》学习,你已经从凡人步入了修仙界,现在你可以尝试去接触一些简单的算法题开始你的修仙生涯了,那今天我们来看看今天的修炼吧⛽⛽⛽

这是是一道非常经典的入门级修炼功法,收录在力扣# 704,而它的名字就已经将写法写在你的脸上了😂——二分查找
ps:工欲善其事必先利其器,一部好的功法可以让你在修仙路上少走许多弯路。😏😏😏
二分查找?
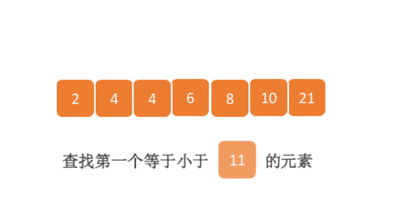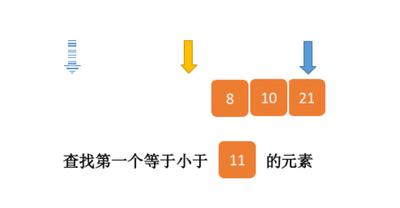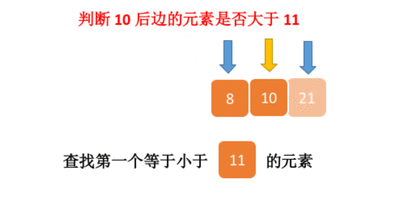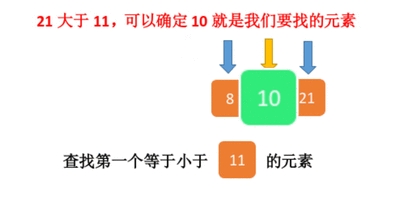
二分查找又称折半查找,优点是比较次数少,查找速度快,平均性能好,占用系统内存较少;其缺点是要求待查表为有序表,且插入删除困难。因此,折半查找方法适用于不经常变动而查找频繁的有序列表。首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。
第一阶段 二分查找?🤔🤔🤔
二分查找的基本思想是将n个元素分成大致相等的两部分,取a[n/2]与x做比较,如果x=a[n/2],则找到x,算法中止;如果x<a[n/2],则只要在数组a的左半部分继续搜索x,如果x>a[n/2],则只要在数组a的右半部搜索x.
因此我们需要left变量middle变量,right变量以及以各target变量
在这个阶段我们需要了解二分查找的基本运算方式,以及需要使用的变量。
第二阶段 易错点😬😬😬
我们应该了解下二分算法的易错点
1.在循环体的跳出判定条件是左边大于等于右边(left>=right)还是左边大于右边(left>right)
2.如果(str[middle]>target),那么接下来我们应该将(middle)更新为(right)还是(right-1)?
问题一:
对待该问题我们需要首先将题意理解清楚,我们根据查找区间分为两种写法——左闭右闭写法和左必右开写法
左闭右闭写法故名思意在该区间我们两头的数都应该取到,我们假设一个这样的区间[1,1],很明显我们的判定条件上必须加上等于,与之相反的当区间为[1,1)左闭右开时我们不能加上等于号。
问题二
应对第二个问题我们只需简单的假设一下当我们使用左闭右闭写法时我们已经判断了(str[middle]>target)那么我们下一次判断的时候就不用该将(middle)加入进去那么自然我们会将(right)更新为(middle-1),当我们使用左闭右开写法时本来定义中就已经不包含(middle)值,那么我们为啥还要将(right)更新为(middle-1)呢?
总结
简单总结一下:
左闭右闭写法——要等于号,并且(middle)应更新为(left=right+1)或(right=middle-1)
左闭右开写法——不要等于号,并且(middle)应更新为(right=middle和(left=middle+1)(这个地方要好好理解下哟)
题目代码(C语言实现)
#include<stdio.h>
#include<string.h>
#define MAX 100000
int search(int* nums, int numsSize, int target)
{int left=0, right, middle;right = numsSize;while (left <= right)//这里是左闭右闭写法{middle = (left + right) / 2;if (*(nums + middle) > target)right = middle - 1;else if (*(nums + middle) < target)left = middle + 1;elsereturn middle;}return -1;//查找失败,无该目标值
}
int main()
{int nums[MAX] = { 0 };int target = 0;int numsSize = 0, i;scanf("%d", &numsSize);//输入区间长度printf("\n");for (i = 0;i < numsSize;i++)scanf("%d", nums + i);//输入查找区间printf("\n");scanf("%d", &target);//输入目标值numsSize = strlen(nums);printf("下标为:%d", search(nums,numsSize,target));}
相关文章:

二分查找——我欲修仙(功法篇)
个人主页:【😊个人主页】 系列专栏:【❤️我欲修仙】 学习名言:临渊羡鱼,不如退而结网——《汉书董仲舒传》 系列文章目录 第一章 ❤️ 二分查找 文章目录系列文章目录前言🚗🚗🚗二分查找&…...

Python 多线程
文章目录一、简介1.1 多线程的特性1.2 GIL二、线程1.2 单线程1.3 多线程三、线程池3.1 pool.submit3.2 pool.map四、Lock(线程锁)4.1 无锁导致的线程资源异常4.2 有锁五、Event(事件)5.1 简介5.2 示例六、Queue(队列&a…...
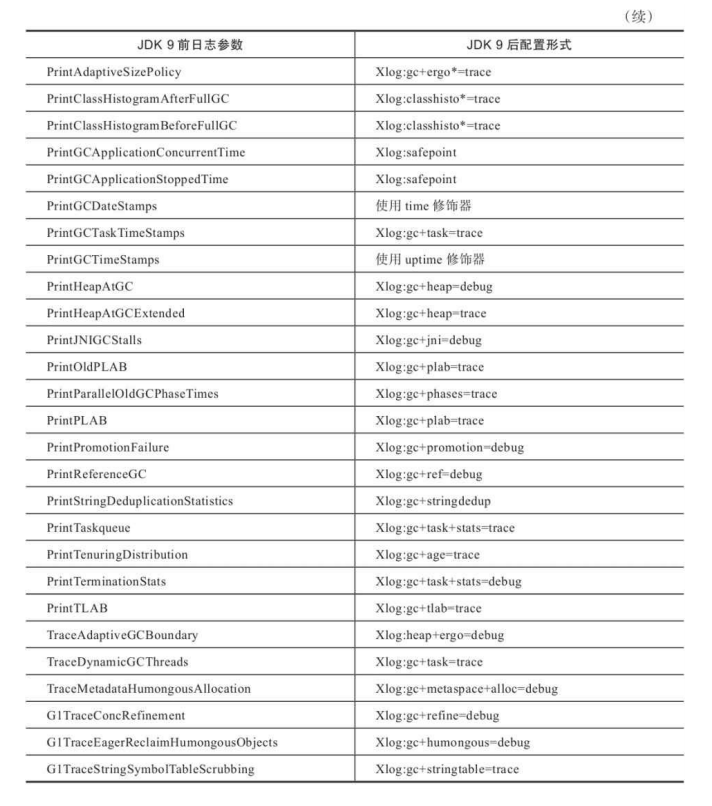
JVM笔记(九)选择合适的垃圾收集器
Epsilon收集器Epsilon收集器由RedHat公司在JEP 318中提出,在此提案里Epsilon被形容成一个无操作的收集器(A No-Op Garbage Collector),而事实上只要Java虚拟机能够工作,垃圾收集器便不可能是真正“无操作”的。原因是“…...

二维图像处理到三维点云处理
一、Opencv和PCL 下面是opencv和pcl的特点、区别和联系的详细对比表格。 特点/区别/联系OpenCVPCL英文全称Open Source Computer Vision LibraryPoint Cloud Library语言C、Python、JavaC功能图像处理(图像处理和分析、特征提取和描述、图像识别和分类、目标检测和跟踪等)、计…...

leetcode 删除有序数组中的重复项
题目 给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。 由于在某些语言中不能改变数组的长度,所以必须将结果放在数组nums的第一…...

JVM学习.03 类加载机制
1、前言从事Java开发工作的都知道,Java程序提交到JVM运行时,需要编译成Class文件,才能被JVM加载运行。那么这些Class文件进入到虚拟机后会发生什么?以及Class是如何被加载的?这些都是本文要讲解的部分。2、类加载时机所…...
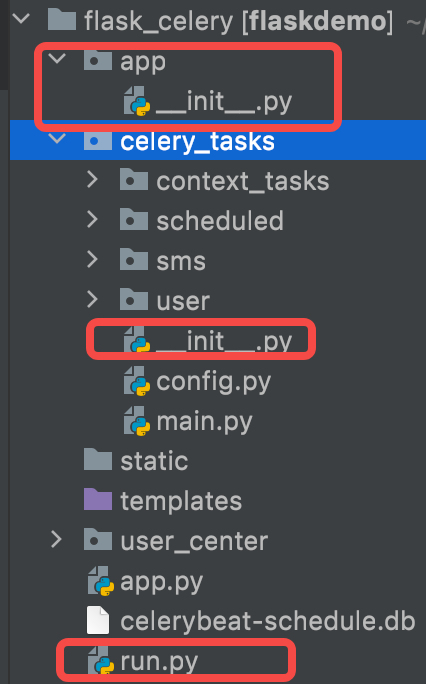
Celery使用:优秀的python异步任务框架
目录Celery 简介介绍安装基本使用Flask使用Celery异步任务定时任务Celery使用Flask上下文进阶使用参考停止Worker后台运行Celery 简介 介绍 Celery 是一个简单、灵活且可靠的,处理大量消息的分布式系统,并且提供维护这样一个系统的必需工具。 它是一个…...
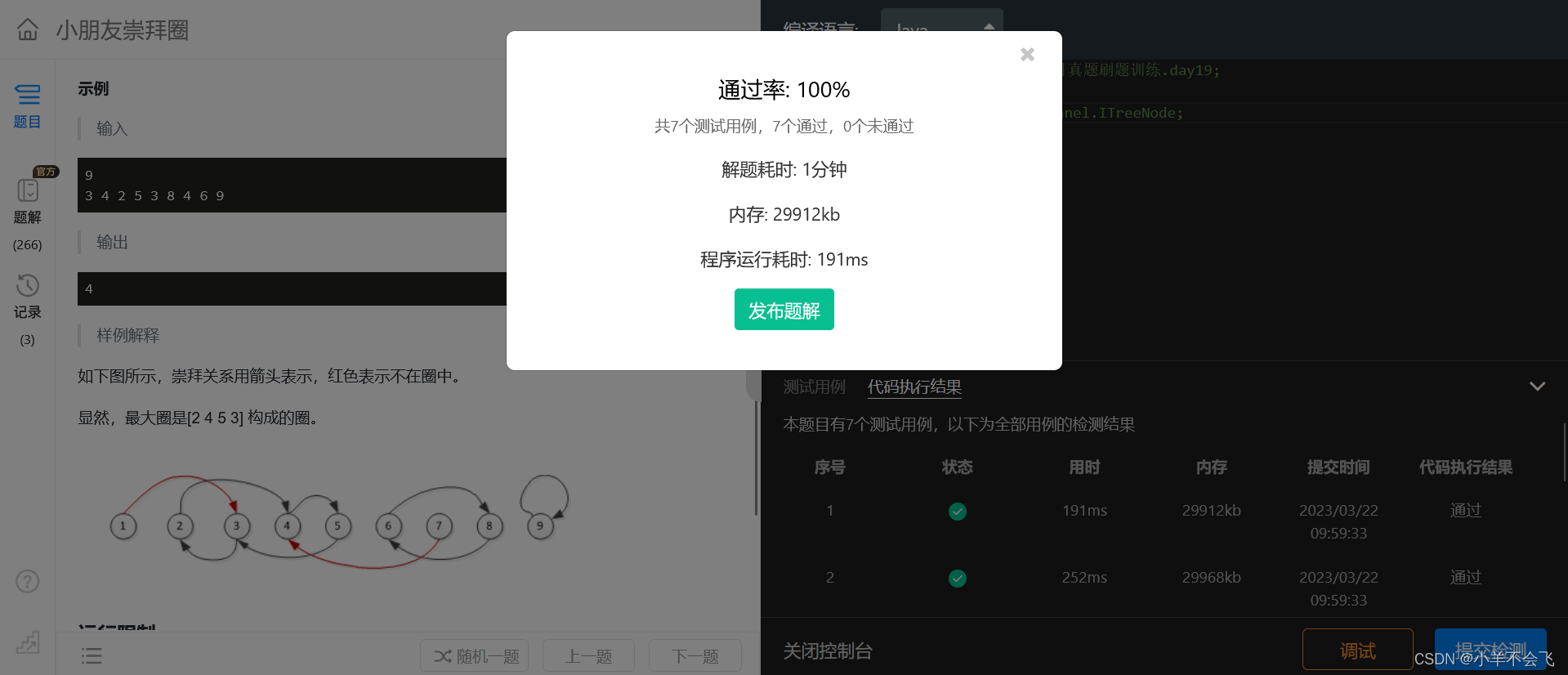
第十四届蓝桥杯三月真题刷题训练——第 19 天
第 1 题:灌溉_BFS板子题 题目描述 小蓝负责花园的灌溉工作。 花园可以看成一个 n 行 m 列的方格图形。中间有一部分位置上安装有出水管。 小蓝可以控制一个按钮同时打开所有的出水管,打开时,有出水管的位置可以被认为已经灌溉好。 每经过一分…...

类和对象 - 下
本文已收录至《C语言》专栏! 作者:ARMCSKGT 目录 前言 正文 初始化列表 成员变量的定义与初始化 初始化列表的使用 变量定义顺序 explicit关键字 隐式类型转换 自定义类型隐式转换 explicit 限制转换 关于static static声明类成员 友元 友…...

【云原生】Linux基础IO(文件理解与操作)
✨个人主页: Yohifo 🎉所属专栏: Linux学习之旅 🎊每篇一句: 图片来源 🎃操作环境: CentOS 7.6 阿里云远程服务器 Great minds discuss ideas. Average minds discuss events. Small minds disc…...

CentOS 7 安装 mysql 8.0 客户端
只想安装 mysql-client 8.0 , 结果发现直接 yum install mysql mysql-client 安装的版本是 mysql Ver 15.1 Distrib 5.5.68-MariaDB ,这个版本太低,连接其他服务器上的 mysql 8.0 时总是失败,因为 mysql 8.0 加密方式改变了&#…...

Ubuntu下载、配置、安装和编译opencv
1 安装相关依赖安装opencv前,需要先准备好编译器、相关依赖sudo apt-get install gcc g cmake vim sudo apt-get install build-essential libgtk2.0-dev libavcodec-dev libavformat-dev libjpeg-dev libswscale-dev libtiff5-dev sudo apt-get install libgtk2.0-…...

第七讲 贪心
文章目录股票买卖 II货仓选址(贪心:排序中位数)糖果传递(❗贪心:中位数)雷达设备(贪心排序)付账问题(平均值排序❓)乘积最大(排序/双指针)后缀表达…...

数字藏品的未来及发展趋势
随着互联网的普及以及数字文化的日益发展,数字藏品作为一种全新的收藏方式正在逐步兴起。数字藏品可以是数字版权、数字艺术品、数字音乐以及数字视频等形式,这些藏品通过数字化技术保存下来,并在互联网上进行传播和交易。数字藏品的发展趋势…...

值得记忆的STL常用算法,分分钟摆脱容器调用的困境,以vector为例,其余容器写法类似
STL常用算法 概述: 算法主要是由头文件<algorithm> <functional> <numeric>组成 <algorithm>是所有STL头文件中最大的一个,范围涉及到比较、交换、查找、遍历操作、复制、修改等等 <nuneric>体积很小,只包括…...
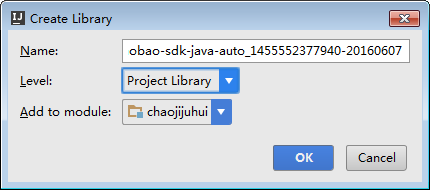
java如何手动导jar包
今天用IDEA,需要导入一个Jar包,因为以前都是用eclipse的,所以对这个idea还不怎么上手,连打个Jar包都是谷歌了一下。 但是发现网上谷歌到的做法一般都是去File –> Project Structure中去设置,有没有如同eclipse一样…...

怎么防止SQL注入?
首先SQL注入是一种常见的安全漏洞,黑客可以通过注入恶意代码来攻击数据库和应用程序。以下是一些防止SQL注入的基本措施: 数据库操作层面 使用参数化查询:参数化查询可以防止SQL注入,因为参数化查询会对用户输入的数据进行过滤和…...
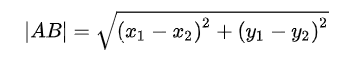
【千题案例】TypeScript获取两点之间的距离 | 中点 | 补点 | 向量 | 角度
我们在编写一些瞄准、绘制、擦除等功能函数时,经常会遇到计算两点之间的一些参数,那本篇文章就来讲一下两点之间的一系列参数计算。 目录 1️⃣ 两点之间的距离 ①实现原理 ②代码实现及结果 2️⃣两点之间的中点 ①实现原理 ②代码实现及结果 3…...
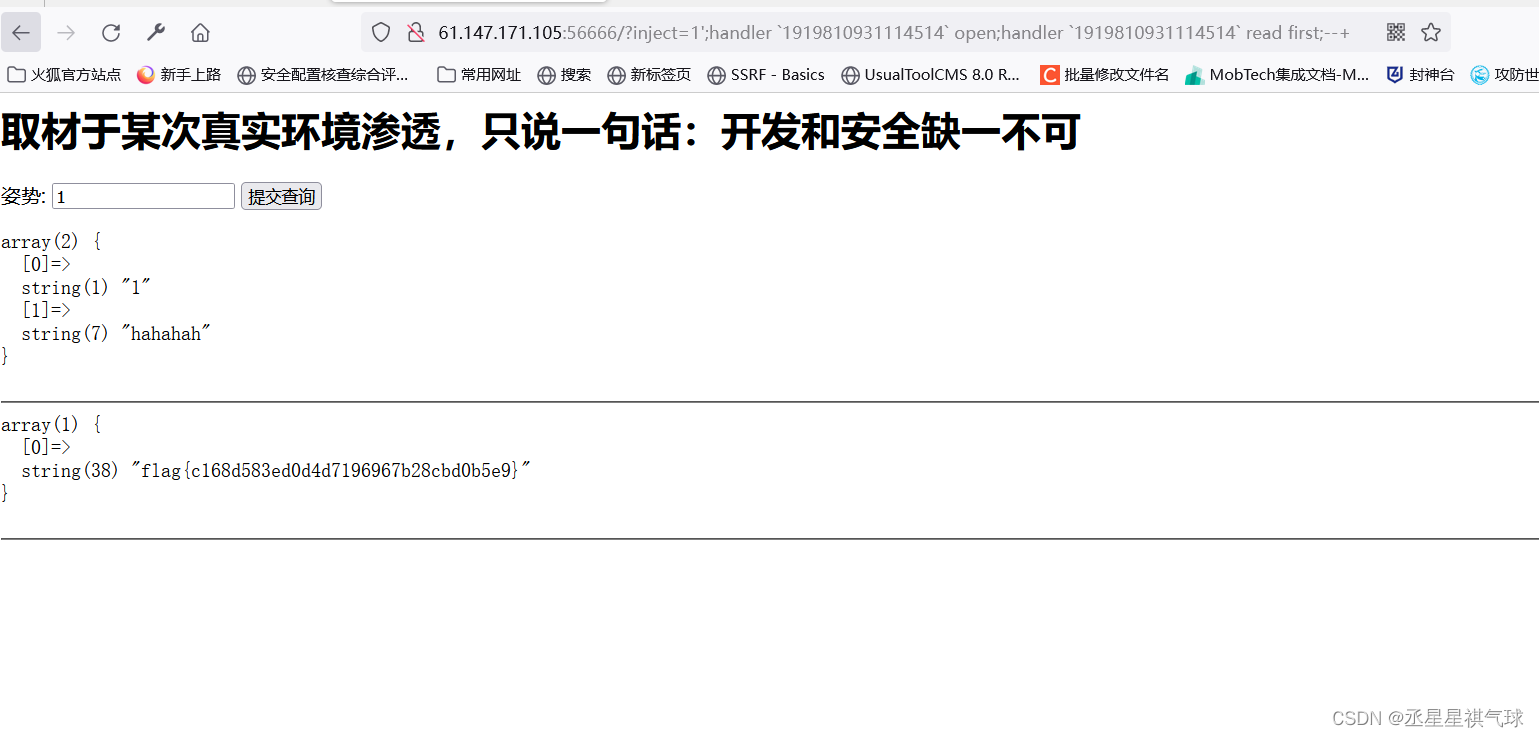
堆叠注入--攻防世界CTF赛题学习
在一次联系CTF赛题中才了解到堆叠注入,在这里简单介绍一下。 堆叠注入的原理什么的一搜一大堆,我就不引用百度了,直接进入正题。 这个是攻防世界的一道CTF赛题。 采用寻常思路来寻找sql注入漏洞。 payload:1 and 11-- 利用payload: and 12…...
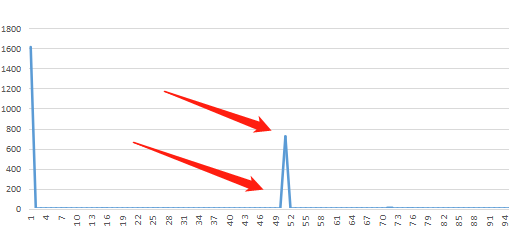
STM32 ADC+定时器+DMA+FFT
本次实现的功能为单片机DAC输出一个正弦波,然后ADC定时采样用DMA输出,最后对DAC输出的波形进行FFT。单片机STM32F103ZET6内部时钟一、配置ADCADC端口为PA1,采用DMA输出,定时器3触发定时器时钟64M,分频后为102.4KHzADC采…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
