dfs和bfs能解决的问题
一.理解暴力穷举之dfs和bfs
暴力穷举
暴力穷举是在解决问题中最常用的手段,而dfs和bfs算法则是这个手段的两个非常重要的工具。
其实,最简单的穷举法是直接遍历,如数列求和,遍历一个数组即可求得所问答案,这与我在前两篇博客中讲述的动态规划算法执行方式其实是一样的,其特点我们说过,有三个“可分解,可一次解决,可储存”,可分解是不管有多大多复杂的数据都能用同一种办法解决的前提,可一次解决,代表每一个子问题的解决答案即是当前最优解,也是全局最优解的子解,这叫做无后效性,无后效性其实表面意思是局部决策对全局决策无关,但准确来说,是局部决策的最优解之外的决策永远不会成为全局决策的子决策,最后若可储存子问题的答案,我们就可以实现直接遍历或动态规划得到我们所需要的答案。
dfs和bfs的特点
在前言我们提到了直接遍历的穷举办法,而动态规划也是其中之一,具有”可分解,可一次解决,可存储“的特点,而dfs和bfs与它们的唯一区别就是”不可一次解决“,也就是并非有最优解,子问题的每一个决策都有可能是全局解的子解,这叫做有后效性,但准确来说,是局部决策都可能会成为全局决策的子决策,那么如何解决这类问题呢,dfs和bfs算法就是这类问题的天敌。
二.掌握dfs和bfs解决问题的方法
1.dfs通过其能够“回溯”的本领解决有后效性
例题

题目链接
分析
题目问的是,在给定n*n棋盘内,棋子位置相互不冲突的情况下,摆放在棋盘区域的棋子个数为k的方案数是多少
1.可先放前面的棋子,再放后面的棋子(可分解)
2.对每个棋盘位置都有放或不放两种决策,每个棋子的这两种决策都可能满足题意(有后效性)
3.在从前到后决策的过程中,可记录已放棋子个数(可存储)
代码
#include<iostream>
#include<cstdio>using namespace std;const int N = 100;
bool col[N],row[N];
char g[N][N];
int cnt = 0,n,m;
void dfs(int x,int y,int k)
{if(x == n) return;if(k == m) {cnt++;return;}if(y == n){y = 0;x++;}dfs(x,y+1,k);//先递归遍历左子树,即不放皇后的操作if(!col[y]&&!row[x]&&(g[x][y] == '#')){col[y] = row[x] = true;dfs(x,y+1,k+1);//再递归遍历右子树col[y] = row[x] = false;}
}
int main()
{while(1){scanf("%d%d",&n,&m);if(n == -1&&m == -1) break;for(int i = 0;i<n;i++)for(int j = 0;j<n;j++)cin>>g[i][j];dfs(0,0,0);printf("%d\n",cnt);cnt = 0;}return 0;
}2.bfs通过其能够“排队”的本领解决有后效性
例题

题目链接
分析
题目问的是,在给定L*R*C迷宫内,从“S”走到“E”至少需要多少分钟
1.可一步一步走(可分解)
2.对每一步都有上下左右前后,每一步的决策都可能满足题意(有后效性)
3.在从前到后决策的过程中,可记录已用掉多少分钟(可存储)
代码
#define _CRT_SECURE_NO_WARNINGS
//#define LOCAL
#include <iostream>
#include <cstring>
#include <queue>
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N=35;
int L,R,C;
int sx,sy,sz,ex,ey,ez;
bool flag;
char g[N][N][N];
bool st[N][N][N];
int dist[N][N][N];
struct Node
{int z,x,y;
};
int dx[]={1,-1,0,0,0,0};
int dy[]={0,0,1,-1,0,0};
int dz[]={0,0,0,0,1,-1};
void bfs(int sz,int sx,int sy)
{memset(dist,0x3f,sizeof dist);Node input;input.z=sz,input.x=sx,input.y=sy;queue<Node>q;q.push(input);st[sz][sx][sy]=1;dist[sz][sx][sy]=0;while(q.size()){Node t=q.front();if(t.z==ez&&t.x==ex&&t.y==ey){flag=1;break;}q.pop();for(int i=0;i<6;i++){int a=t.z+dz[i];int b=t.x+dx[i];int c=t.y+dy[i];if(a<0||b<0||c<0||a>=L||b>=R||c>=C)continue;if(st[a][b][c]||g[a][b][c]=='#')continue;st[a][b][c]=1;Node tmp;tmp.z=a,tmp.x=b,tmp.y=c;q.push(tmp);dist[a][b][c]=dist[t.z][t.x][t.y]+1;}}
}
void solve()
{while(~scanf("%d%d%d",&L,&R,&C)&&(L||R||C)){for(int i=0;i<L;i++)for(int j=0;j<R;j++)scanf("%s",g[i][j]);for(int i=0;i<L;i++)for(int j=0;j<R;j++)for(int k=0;k<C;k++){if(g[i][j][k]=='S')sz=i,sx=j,sy=k;if(g[i][j][k]=='E')ez=i,ex=j,ey=k;}memset(st,0,sizeof st);flag=0;bfs(sz,sx,sy);if(flag) printf("Escaped in %d minute(s).\n",dist[ez][ex][ey]);else puts("Trapped!");}return;
}int main()
{
#ifdef LOCALfreopen("data.in", "r", stdin);freopen("data.out", "w", stdout);
#endifint t = 1;//cin>>t;while(t--){solve();}return 0;
}
~感谢观看❥(^_-)
相关文章:

dfs和bfs能解决的问题
一.理解暴力穷举之dfs和bfs暴力穷举暴力穷举是在解决问题中最常用的手段,而dfs和bfs算法则是这个手段的两个非常重要的工具。其实,最简单的穷举法是直接遍历,如数列求和,遍历一个数组即可求得所问答案,这与我在前两篇博…...

静态通讯录,适合初学者的手把手一条龙讲解
数据结构的顺序表和链表是一个比较困难的点,初见会让我们觉得有点困难,正巧C语言中有一个类似于顺序表和链表的小程序——通讯录。我们今天就来讲一讲通讯录的实现,也有利于之后顺序表和链表的学习。 目录 0.通讯录的初始化 1.菜单的创建…...
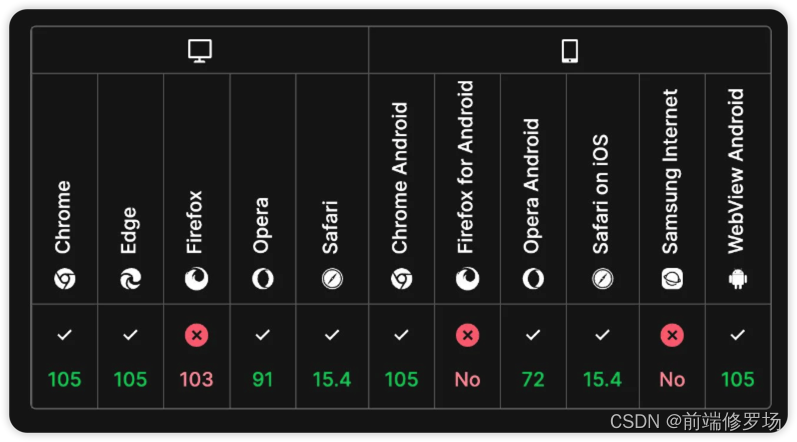
【你不知道的 CSS】你写的 CSS 太过冗余,以至于我对它下手了
:is() 你是否曾经写过下方这样冗余的CSS选择器: .active a, .active button, .active label {color: steelblue; }其实上面这段代码可以这样写: .active :is(a, button, label) {color: steelblue; }看~是不是简洁了很多! 是的,你可以使用…...

Lesson 8.1 决策树的核心思想与建模流程
文章目录一、借助逻辑回归构建决策树1. 决策树实例2. 决策树知识补充2.1 决策树简单构建2.2 决策树的分类过程2.3 决策树模型本质2.4 决策树的树生长过程2.5 树模型的基本结构二、决策树的分类与流派1. ID3(Iterative Dichotomiser 3) 、C4.5、C5.0 决策树2. CART 决策树3. CHA…...

【算法】FIFO先来先淘汰算法分析和编码实战
背景 在设计一个系统的时候,由于数据库的读取速度远小于内存的读取速度 为加快读取速度,将一部分数据放到内存中称为缓存,但内存容量是有限的,当要缓存的数据超出容量,就需要删除部分数据 这时候需要设计一种淘汰机制…...
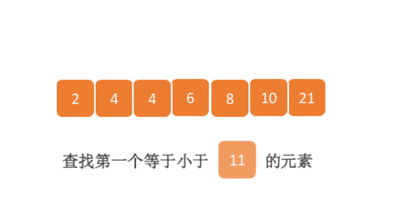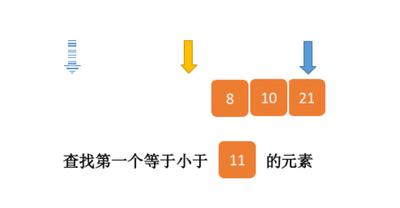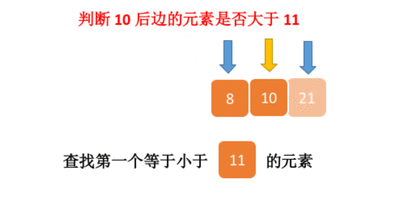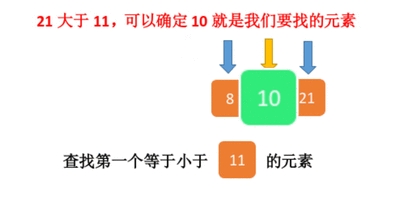
二分查找——我欲修仙(功法篇)
个人主页:【😊个人主页】 系列专栏:【❤️我欲修仙】 学习名言:临渊羡鱼,不如退而结网——《汉书董仲舒传》 系列文章目录 第一章 ❤️ 二分查找 文章目录系列文章目录前言🚗🚗🚗二分查找&…...

Python 多线程
文章目录一、简介1.1 多线程的特性1.2 GIL二、线程1.2 单线程1.3 多线程三、线程池3.1 pool.submit3.2 pool.map四、Lock(线程锁)4.1 无锁导致的线程资源异常4.2 有锁五、Event(事件)5.1 简介5.2 示例六、Queue(队列&a…...
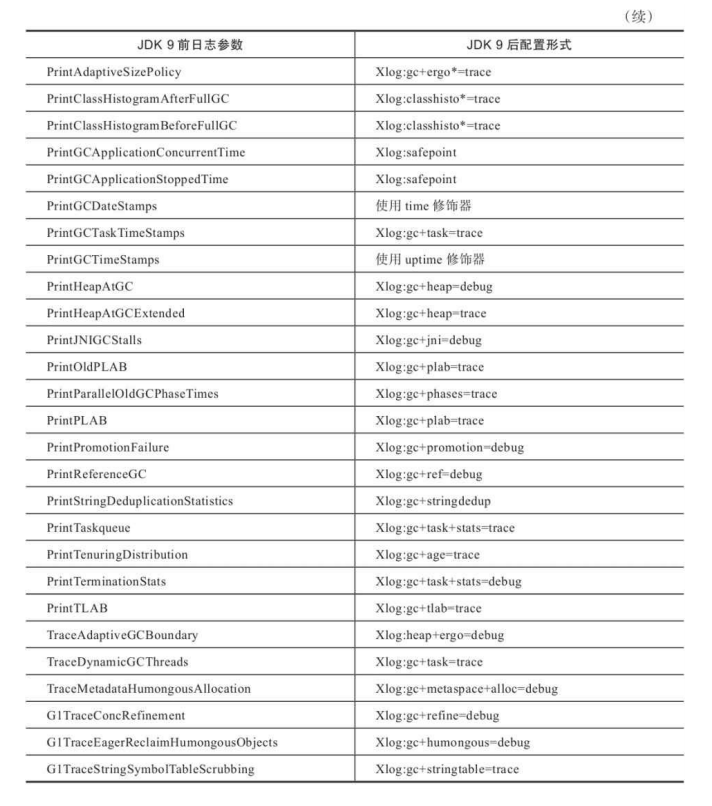
JVM笔记(九)选择合适的垃圾收集器
Epsilon收集器Epsilon收集器由RedHat公司在JEP 318中提出,在此提案里Epsilon被形容成一个无操作的收集器(A No-Op Garbage Collector),而事实上只要Java虚拟机能够工作,垃圾收集器便不可能是真正“无操作”的。原因是“…...

二维图像处理到三维点云处理
一、Opencv和PCL 下面是opencv和pcl的特点、区别和联系的详细对比表格。 特点/区别/联系OpenCVPCL英文全称Open Source Computer Vision LibraryPoint Cloud Library语言C、Python、JavaC功能图像处理(图像处理和分析、特征提取和描述、图像识别和分类、目标检测和跟踪等)、计…...

leetcode 删除有序数组中的重复项
题目 给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。 由于在某些语言中不能改变数组的长度,所以必须将结果放在数组nums的第一…...

JVM学习.03 类加载机制
1、前言从事Java开发工作的都知道,Java程序提交到JVM运行时,需要编译成Class文件,才能被JVM加载运行。那么这些Class文件进入到虚拟机后会发生什么?以及Class是如何被加载的?这些都是本文要讲解的部分。2、类加载时机所…...
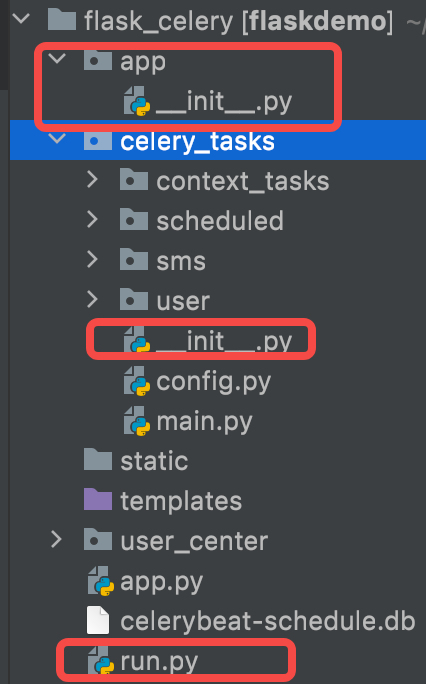
Celery使用:优秀的python异步任务框架
目录Celery 简介介绍安装基本使用Flask使用Celery异步任务定时任务Celery使用Flask上下文进阶使用参考停止Worker后台运行Celery 简介 介绍 Celery 是一个简单、灵活且可靠的,处理大量消息的分布式系统,并且提供维护这样一个系统的必需工具。 它是一个…...
第十四届蓝桥杯三月真题刷题训练——第 19 天
第 1 题:灌溉_BFS板子题 题目描述 小蓝负责花园的灌溉工作。 花园可以看成一个 n 行 m 列的方格图形。中间有一部分位置上安装有出水管。 小蓝可以控制一个按钮同时打开所有的出水管,打开时,有出水管的位置可以被认为已经灌溉好。 每经过一分…...

类和对象 - 下
本文已收录至《C语言》专栏! 作者:ARMCSKGT 目录 前言 正文 初始化列表 成员变量的定义与初始化 初始化列表的使用 变量定义顺序 explicit关键字 隐式类型转换 自定义类型隐式转换 explicit 限制转换 关于static static声明类成员 友元 友…...

【云原生】Linux基础IO(文件理解与操作)
✨个人主页: Yohifo 🎉所属专栏: Linux学习之旅 🎊每篇一句: 图片来源 🎃操作环境: CentOS 7.6 阿里云远程服务器 Great minds discuss ideas. Average minds discuss events. Small minds disc…...

CentOS 7 安装 mysql 8.0 客户端
只想安装 mysql-client 8.0 , 结果发现直接 yum install mysql mysql-client 安装的版本是 mysql Ver 15.1 Distrib 5.5.68-MariaDB ,这个版本太低,连接其他服务器上的 mysql 8.0 时总是失败,因为 mysql 8.0 加密方式改变了&#…...

Ubuntu下载、配置、安装和编译opencv
1 安装相关依赖安装opencv前,需要先准备好编译器、相关依赖sudo apt-get install gcc g cmake vim sudo apt-get install build-essential libgtk2.0-dev libavcodec-dev libavformat-dev libjpeg-dev libswscale-dev libtiff5-dev sudo apt-get install libgtk2.0-…...

第七讲 贪心
文章目录股票买卖 II货仓选址(贪心:排序中位数)糖果传递(❗贪心:中位数)雷达设备(贪心排序)付账问题(平均值排序❓)乘积最大(排序/双指针)后缀表达…...

数字藏品的未来及发展趋势
随着互联网的普及以及数字文化的日益发展,数字藏品作为一种全新的收藏方式正在逐步兴起。数字藏品可以是数字版权、数字艺术品、数字音乐以及数字视频等形式,这些藏品通过数字化技术保存下来,并在互联网上进行传播和交易。数字藏品的发展趋势…...

值得记忆的STL常用算法,分分钟摆脱容器调用的困境,以vector为例,其余容器写法类似
STL常用算法 概述: 算法主要是由头文件<algorithm> <functional> <numeric>组成 <algorithm>是所有STL头文件中最大的一个,范围涉及到比较、交换、查找、遍历操作、复制、修改等等 <nuneric>体积很小,只包括…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
