数据结构--数据结构概述
一、数据结构三要素
1. 数据的逻辑结构
数据的逻辑结构是指数据元素之间的关系和组织方式,通常分为线性结构和非线性结构。
-
线性结构:例如线性表,其中数据元素按照顺序排列,彼此之间存在一对一的关系。
-
非线性结构:例如集合、树和图,这些结构中的数据元素之间的关系更加复杂,可能存在一对多或多对多的关系。

2. 数据的存储结构
1. 顺序存储
顺序存储是一种将数据元素按照线性顺序依次存放在一块连续的内存空间中的存储方式。它的优点在于可以通过简单的下标访问实现快速的随机访问,适合存储固定大小的数据结构,如数组。然而,顺序存储在插入和删除操作时可能会导致大量的数据移动,效率较低。
2. 链式存储
链式存储是一种将数据元素以节点的形式存放在不连续的内存空间中,每个节点包含数据部分和指向下一个节点的指针。该方式的优点在于动态内存分配,灵活性高,适合频繁插入和删除操作。链式存储的缺点是随机访问效率较低,因为需要从头节点开始逐个遍历。
3. 索引存储
索引存储是一种结合了顺序存储和链式存储优点的数据存储方式。它通过建立索引表来加速数据的查找,索引表中的每个条目指向数据存储的具体位置。该方式能够在保持较快查找速度的同时,支持高效的数据插入和删除操作。然而,索引存储需要额外的空间来维护索引,增加了存储的复杂性。
4. 散列存储
散列存储是一种通过散列函数将数据映射到固定大小的数组中存储的方式。它能够实现快速的查找、插入和删除操作,适合处理大量数据。散列存储的主要挑战在于处理哈希冲突,即不同的数据可能会被映射到相同的存储位置。常用的解决方法包括链式法和开放地址法。尽管散列存储在查找效率上表现优异,但在实现上相对复杂,并且需要合理设计散列函数以减少冲突。
3. 数据的运算
数据的运算是指对数据结构中的数据进行各种操作的过程,包括插入、删除、查找、更新等。这些运算的效率往往依赖于所选用的数据结构和存储方式,因此在设计数据结构时需充分考虑运算的需求和性能。
二、算法
1. 算法的五个重要特性
-
确定性:每个算法的步骤必须是明确的,不能存在模糊或含糊的描述。每一步操作都应清晰、具体,确保在任何情况下都能被准确理解和执行。
-
有穷性:算法必须在有限的步骤内终止。换句话说,算法不能无限循环,必须在经过有限的操作后得出结果。这一特性保证了算法的可执行性和有效性。
-
输入:一个算法可以有零个或多个输入,这些输入是算法执行所需的数据。输入可以是外部提供的,也可以是算法内部生成的,但无论如何,算法必须能够接收并处理这些输入。
-
输出:算法必须能够产生至少一个输出,输出是算法对输入进行处理后得到的结果。输出的形式和数量取决于算法的设计和具体问题的要求。
-
可行性:算法中的每一步操作都必须是可行的,能够在合理的时间内执行。有效性确保了算法不仅在理论上可行,而且在实践中能够被实现,并在合理的时间内完成计算。
2. 算法应考虑的目标
-
可读性:算法的可读性是指算法的清晰程度和易于理解的程度。一个可读性高的算法能够让其他开发者或用户轻松理解其逻辑和流程。这对于团队协作和后续维护非常重要。
-
正确性:算法的正确性是指算法能够在所有有效输入下产生正确的输出。一个正确的算法应能准确解决所设计的问题,并满足预期的功能需求。确保正确性通常需要充分的测试和验证。
-
健壮性:健壮性是指算法在面对异常输入或意外情况时的表现能力。一个健壮的算法能够处理各种边界情况、错误输入或系统故障,而不会导致崩溃或产生错误结果。这种特性对于提升用户体验和系统稳定性至关重要。
-
高效率与低存储量需求:高效率指算法在执行时能够快速完成任务,通常涉及时间复杂度的优化。低存储量需求则是指算法在运行时对内存的占用要尽量少。一个高效且节省存储的算法能够在处理大规模数据时表现出色,降低资源消耗。
3. 时间复杂度
定义:时间复杂度是用来描述算法执行所需时间的一个函数,通常用大O符号表示。它表示输入规模(通常用 n 表示)增长时,算法执行时间的增长率。
分析方式:
- 最坏情况:考虑输入数据中最不利的情况,通常用于评估算法的上限。
- 最好情况:考虑输入数据中最有利的情况,评估算法的下限。
- 平均情况:考虑所有可能输入的平均执行时间,用于评估算法的期望性能。
常见时间复杂度的分类:
- 常数时间:O(1) - 不随输入规模变化而变化,例如访问数组中的某个元素。
- 对数时间:O(log n) - 例如二分查找。
- 线性时间:O(n) - 例如遍历数组。
- 线性对数时间:O(nlogn) - 例如高效排序算法(如归并排序和快速排序)。
- 平方时间:O(n^2) - 例如冒泡排序和选择排序。
- 指数时间:O(2^n) - 例如某些递归算法(如斐波那契数列的朴素实现)。
- 阶乘时间:O(n!) - 例如解决旅行商问题的某些算法。
重要性:时间复杂度帮助我们理解算法在处理不同规模输入时的性能表现,从而选择合适的算法以提高应用程序的响应速度和用户体验。
4. 空间复杂度
定义:空间复杂度是用来描述算法在执行过程中所需内存空间的一个函数,同样通常用大O符号表示。它表示随着输入规模的增加,算法所需的存储空间的增长率。
分析方式:
- 固定部分:与输入规模无关的空间需求,例如常量空间、固定大小的变量等。
- 可变部分:与输入规模相关的空间需求,例如动态分配的数组、递归调用栈等。
常见空间复杂度的分类:
- 常数空间:O(1) - 例如只使用固定数量的变量。
- 线性空间:O(n) - 例如使用一个数组来存储输入数据。
- 平方空间:O(n^2) - 例如在某些算法中使用的二维数组。
重要性:空间复杂度帮助我们理解算法在内存使用方面的效率,尤其在处理大数据集时,合理的空间使用可以避免内存溢出和提高程序的运行效率。
相关文章:

数据结构--数据结构概述
一、数据结构三要素 1. 数据的逻辑结构 数据的逻辑结构是指数据元素之间的关系和组织方式,通常分为线性结构和非线性结构。 线性结构:例如线性表,其中数据元素按照顺序排列,彼此之间存在一对一的关系。 非线性结构:…...

Spring中的BeanFactoryAware
BeanFactoryAware 是 Spring 框架中的一个接口,用于在 Spring 容器中获取 BeanFactory 实例。实现这个接口的类可以在其属性被设置后获取到 BeanFactory,从而可以访问 Spring 容器中的其他 bean。 BeanFactoryAware 接口概述 BeanFactoryAware 接口位于…...

Neo4j service is not installed
问题: Starting Neo4j. Neo4j service is not installed Unable to start. See user log for details. Run with --verbose for a more detailed error message.解决: neo4j windows-service install neo4j start ok了...
)
LeetCode 3132.找出与数组相加的整数 II:排序+3次尝试(nlog n)
【LetMeFly】3132.找出与数组相加的整数 II:排序3次尝试(nlog n) 力扣题目链接:https://leetcode.cn/problems/find-the-integer-added-to-array-ii/ 给你两个整数数组 nums1 和 nums2。 从 nums1 中移除两个元素,并且所有其他元素都与变量…...

微信小程序--26(全局配置-1)
一、全局配置文件 1.标志 app.json 2.配置项 pages 记录当前小程序所有页面的存放路径 window 全局配置小程序窗口配置 tabBar 设置小程序底部的tabBar效果 style 是否启用新版本的组将样式 3.window 导航栏区域 navigationBar …...

汽车4S店管理系统-计算机毕设Java|springboot实战项目
🍊作者:计算机毕设残哥 🍊简介:毕业后就一直专业从事计算机软件程序开发,至今也有8年工作经验。擅长Java、Python、微信小程序、安卓、大数据、PHP、.NET|C#、Golang等。 擅长:按照需求定制化开发项目、 源…...

bug的常见排查和分析思路以及相关的原因分类
作为开发人员,经常会收到来自用户和QA,领导反馈的各种问题。 为了快速问题,我们有时需要站在更高的角度,更全面的看待问题。才能更快锁定问题。 具体的bug还需要结合企业实际业务情况,相关的框架,依赖库&…...

Nature:7个提升科研产出的实用建议
我是娜姐 迪娜学姐 ,一个SCI医学期刊编辑,探索用AI工具提效论文写作和发表。 一个值得思考的问题是:层出不穷的效率工具到底是提升还是降低了科研产出? 大学教授萨拉 (Sara) 描述了她典型的工作日场景:"…...

react-native从入门到实战系列教程-页面之间的跳转
路由的跳转,是app开发中需要处理的问题,一个页面不可能装下那么多的内容。在react-native中,我们使用的路由组件跟reactjs中还是有区别的,这里贴出官网的文档:https://reactnavigation.org/docs/navigating 实现效果 安装 按照官网的指导安装即可。代码实现 app.jsx中改造…...

HarmonyOS应用开发者高级认证(一)
1、依次点击A、B、C、D四个按钮,其中不会触发UI刷新的是: 答案: Button("C").onClick(() > {this.nameList[0].name "Jim"})分析:直接更新非一级数据不会触发UI刷新 2、如果要实现Row组件内的子元素均匀…...

【网络】套接字(socket)编程——UDP版
1.socket 1.1.什么是socket Socket 的中文翻译过来就是“套接字”。 套接字是什么,我们先来看看它的英文含义:插座。 Socket 就像一个电话插座,负责连通两端的电话,进行点对点通信,让电话可以进行通信,端…...

一篇文章让你彻底掌握 Shell
大家好,这里是 Lucifer三思而后行,专注于提升数据库运维效率。 文章目录 一篇文章让你彻底掌握 Shell简介什么是 shell什么是 shell 脚本Shell 环境指定脚本解释器 模式交互模式非交互模式 基本语法解释器注释echoprintfprintf 的转义符 变量变量命名原则…...

Java中的Collection集合:深入理解与应用
在Java中,Collection接口是Java集合框架(Java Collections Framework)的基石之一,它定义了一系列操作对象集合的方法,如添加、删除、遍历等。Collection接口是List、Set和Queue等具体集合类型的父接口,为Ja…...
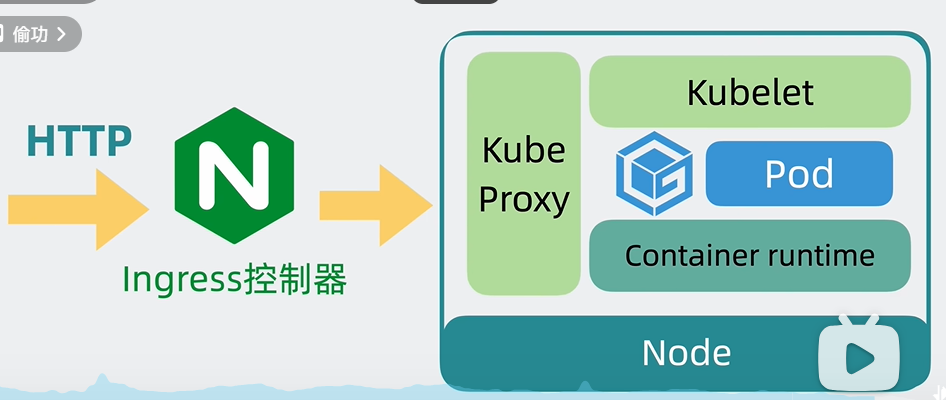
Kubernetes-K8S
Kubernetes由于单词太长,省略掉中间8个字母简称为K8S。它介于应用服务和服务器之间。能够通过策略协调和管理多个服务,只需要一个YAML文件配置。定义应用的部署顺序等信息,自动部署应用到各个服务器,还可以自动扩容缩容。 架构原理…...
简化文本处理流程,通用文字识别助力提升信息采集效率
随着信息技术的发展、移动设备使用的普及和全球化的商业需求,非结构化数据转换为结构化数据的需求日益增长,数字化成为信息存储和管理的主流趋势。在此背景下,OCR技术应运而生,该技术可以将图像中文本信息转化为计算机等设备可以使…...

【网络】TCP协议通信的重要策略——滑动窗口,快重传,流量控制,拥塞控制,延时应答
目录 MSS值 滑动窗口 滑动窗口与重发机制 快重传机制 滑动窗口与流量控制 滑动窗口与拥塞控制 延时应答 个人主页:东洛的克莱斯韦克-CSDN博客 相关文章 【网络】传输层TCP协议的报头和传输机制-CSDN博客 【网络】详解TCP协议通信时客户/服务端的状态-CSDN博…...

极狐GitLab CI/CD 如何构建镜像并推送到 azure 镜像仓库?
极狐GitLab 是 GitLab 在中国的发行版,专门面向中国程序员和企业提供企业级一体化 DevOps 平台,用来帮助用户实现需求管理、源代码托管、CI/CD、安全合规,而且所有的操作都是在一个平台上进行,省事省心省钱。可以一键安装极狐GitL…...

Leetcode—1143. 最长公共子序列【中等】
2024每日刷题(155) Leetcode—1143. 最长公共子序列 实现代码 class Solution { public:int longestCommonSubsequence(string text1, string text2) {int m text1.length();int n text2.length();vector<vector<int>> dp(m 1, vector&…...

ZBrush笔刷介绍
根据使用的方法和效果,ZBrush的笔刷可以分类如下: 基本功能笔刷 这些笔刷用于常规的雕刻、移动和平滑操作。 纹理应用笔刷 一般需要自己额外购买的是这三种笔刷 Alpha Brushes:使用灰度图(alpha)来定义笔刷形状和纹…...

React+AntDesign做一个日历,展示节假日,节气,并且在某几个时间上添加活动备注
直接贴效果图😄 首先日历是用的AntDesign提供的Calendar组件,这个组件还是蛮强大的,可以自定义头部时间下拉;渲染每个时间段,或者重置时间段内容,玩的空间是很大的 直接贴代码,结尾最后我会将…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...
