leetcode39组合总和

题目描述

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。 对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：
输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

解题思路

回溯算法：这类问题的典型解法是使用回溯算法，递归地构建可能的组合，并在找到符合条件的组合时将其加入结果集。
剪枝：为了优化算法，我们可以对已经超过目标值的组合进行剪枝，避免无效的递归。
排序：先对候选数字排序，方便后续的剪枝操作。

解题步骤

1.排序候选数字：为了方便剪枝操作，先将候选数字排序。排序后的候选数字为 [3, 4, 7, 8]。
2.回溯查找组合：从第一个候选数字开始，尝试所有可能的组合，计算每个组合的和。如果和等于目标值，则将其添加到结果集。如果和超过目标值，则停止当前路径的搜索（剪枝）。

代码实现

func combinationSum(candidates []int, target int) [][]int {// 1.初始化var result [][]intvar combination []int// 2.排序以便于剪枝sort.Ints(candidates)// 3.声明一个回溯函数var backtrack func(start, target int)backtrack = func(start, target int) {if target == 0 {// 4.找到一个符合条件的组合，加入结果集result = append(result, append([]int(nil), combination...))return}for i := start; i < len(candidates); i++ {if candidates[i] > target {// 5.剪枝：如果当前候选数字大于剩余目标值，直接退出循环break}// 6.选择当前候选数字combination = append(combination, candidates[i])// 7.因为数字可以重复使用，所以传入 i 作为下一个开始索引backtrack(i, target-candidates[i])// 8.回溯：撤销选择combination = combination[:len(combination)-1]}}// 9.回溯backtrack(0, target)// 10.返回结果return result
}

代码测试

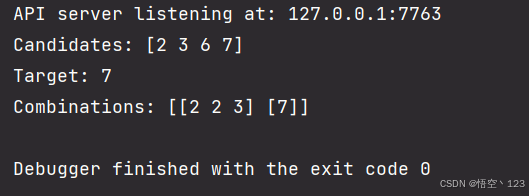
func main() {// 测试用例candidates := []int{2, 3, 6, 7}target := 7// 打印结果fmt.Println("Candidates:", candidates)fmt.Println("Target:", target)fmt.Println("Combinations:", combinationSum(candidates, target))
}

测试结果

关于题目疑问

Q1 为什么用回溯来解决这个问题？

1. 问题的本质是枚举所有可能的组合
   这道题的目标是找出所有数字组合，使得这些组合的数字之和等于目标值。这类问题的本质是需要枚举所有可能的组合，并对每个组合进行验证。回溯算法擅长于这种“试探并撤销”的过程，可以系统地枚举所有可能的解。

2. 回溯算法可以有效地处理组合问题
   回溯算法通过递归地构建解空间树（每个节点表示一个选择），探索每一个可能的选择路径。当发现某条路径不能满足条件时，算法会“回溯”到上一步，尝试其他路径。
   递归的便利性：回溯算法可以自然地处理递归场景，例如在组合问题中，通过递归函数，我们可以方便地处理当前组合中的每一个元素，并且可以灵活地调整递归函数的参数来处理不同的子问题。
   逐步构建解的能力：回溯算法可以逐步构建可能的解，并在找到满足条件的解时立即将其记录下来。同时，如果当前路径已经不可能生成一个有效的解，回溯算法可以立刻剪枝并返回到上一个状态，从而避免不必要的计算。

3. 剪枝优化减少不必要的计算
   在回溯算法中，剪枝是一种重要的优化技术。通过剪枝，可以在搜索空间过大时，排除那些明显不可能产生有效解的路径，从而减少计算量。
   排序+剪枝：在这道题中，先对候选数组进行排序，然后在递归中，如果当前选择的数字已经超过了剩余的目标值，我们就可以直接停止对该路径的探索，因为后续的数字只会更大，不可能满足要求。这大大提高了效率。

4. 灵活性和通用性
   回溯算法不仅能解决这道题，还能适应很多类似的组合问题。例如，LeetCode 上的许多其他组合、排列、子集问题（如组合总和 II、全排列、子集等）都可以通过回溯算法解决。回溯算法的灵活性和通用性使它成为处理这类问题的首选。

5. 易于理解和实现
   尽管回溯算法在最坏情况下的时间复杂度较高，但它相对容易理解和实现。特别是在找出所有解的情况下，回溯算法的逻辑是清晰的：尝试每一个可能的路径，直到找到所有符合条件的路径为止。

结论
回溯算法之所以适合用来解决这道题，是因为它能够系统地、全面地遍历所有可能的组合，并且在找到不符合条件的路径时，可以迅速回退并尝试其他路径。结合剪枝等优化措施，回溯算法能够在保持简洁明了的同时，尽可能地高效地解决问题。这使得回溯算法成为解决组合总和问题的理想选择。

Q2 回溯过程是怎样的？

回溯过程详细解释
我们以代码中 combinationSum 函数的 backtrack 递归函数为例，假设输入的 candidates 为 [2, 3, 6, 7]，target 为 7。
初始状态
candidates: [2, 3, 6, 7]
target: 7
combination: []（当前组合，开始时为空）
result: []（存储所有符合条件的组合）
回溯的每一步
第一层递归（从 candidates[0] 开始）
选择 2：combination = [2]，新的 target = 7 - 2 = 5。
继续调用 backtrack(0, 5)。
第二层递归（仍然从 candidates[0] 开始）
选择 2：combination = [2, 2]，新的 target = 5 - 2 = 3。
继续调用 backtrack(0, 3)。
第三层递归（仍然从 candidates[0] 开始）
选择 2：combination = [2, 2, 2]，新的 target = 3 - 2 = 1。
继续调用 backtrack(0, 1)。
第四层递归（仍然从 candidates[0] 开始）
选择 2：combination = [2, 2, 2, 2]，新的 target = 1 - 2 = -1。
由于 target 小于 0，回溯：移除最后一个 2，组合变回 combination = [2, 2, 2]，然后尝试 candidates[1]。
尝试 candidates[1]（在第三层递归中）
选择 3：combination = [2, 2, 3]，新的 target = 3 - 3 = 0。
由于 target 等于 0，将 [2, 2, 3] 加入 result。
回溯：移除 3，组合变回 combination = [2, 2]。
继续尝试 candidates[2] 和 candidates[3]（在第二层递归中）
发现它们都使 target 小于 0，所以不进一步递归，继续回溯。
回到第一层递归（尝试 candidates[1]）
选择 3：combination = [3]，新的 target = 7 - 3 = 4。
继续调用 backtrack(1, 4)，接下来的步骤类似，尝试不同组合。
尝试 candidates[2] 和 candidates[3]
combination = [6]，combination = [7] 最终找到另一个组合 [7]。
回溯树的结构
第一层选择 2，进行回溯，深度优先搜索所有可能的组合。
回溯到第一层，选择 3，然后继续尝试。
最终遍历所有可能的组合，找到满足条件的组合 [2, 2, 3] 和 [7]。
总结
选择：在每一步，我们选择一个候选数字，并将其加入当前组合。
递归：对新组合进行递归，尝试构造下一个数字。
剪枝：如果当前组合的和超过目标值，我们停止递归并回溯。
回溯：如果递归到达底部但不符合条件（和超过或等于目标值），我们回到上一步，撤销上一步的选择，尝试下一个候选数字。
通过这样不断尝试、撤销的过程，算法能够遍历所有可能的组合，最终得到所有符合条件的结果。

Q3 []int(nil) 的含义？

[]int(nil) 是一种显式创建 nil 切片的方式。它的作用等同于 var s []int，即创建一个 nil 切片。

为什么使用nil?

在 Go 语言中，切片是一种动态数组，它本质上是对数组的一个引用。切片有三个字段：指向数组的指针、切片的长度、和切片的容量。
nil 切片：一个 nil 切片是一个没有分配底层数组的切片，它的长度和容量都为 0。你可以通过 var s []int 或 s := []int(nil) 来声明一个 nil 切片。

var s []int
fmt.Println(s == nil) // true

在某些情况下，尤其是在回溯算法中，我们需要确保创建的是一个空切片（而不是一个已经被初始化的非 nil 的切片）。[]int(nil) 显式地创建一个 nil 切片，这样在后续的操作中，可以避免不必要的内存分配或初始化。

result = append(result, append([]int(nil), combination...))

[]int(nil) 创建了一个 nil 切片。
append([]int(nil), combination…) 创建了一个包含 combination 元素的新切片，这个新切片和 combination 不共享底层数组，是一个独立的拷贝。

与空切片 []int{} 的区别?

虽然 []int(nil) 和 []int{} 都可以用于创建空切片，但它们在初始化时的内存分配行为略有不同：
[]int(nil)：创建的是一个 nil 切片，没有分配任何底层数组。这个切片的长度和容量为 0，并且底层数组指针为 nil。
[]int{}：创建的是一个非 nil 的空切片，它的长度为 0，容量也为 0，但底层数组指针不为 nil（尽管该数组本身为空）。
在实际编程中，选择 []int(nil) 还是 []int{} 主要取决于具体的需求。例如，如果你希望确保切片是 nil（比如用于判断或处理），可以使用 []int(nil)；如果你只是需要一个空的可用切片，则使用 []int{}。