宝兰德荣获openEuler项目群青铜捐赠人称号,共筑开源生态繁荣新篇章
近日,开放原子开源基金会正式公布了新增捐赠人名单,宝兰德凭借在开源领域的卓越贡献与深厚实力,被授予openEuler项目群青铜捐赠人称号。

开放原子开源基金会是致力于推动全球开源事业发展的非营利机构,于2020年6月在北京成立。开放原子开源基金会本着以开发者为本的开源项目孵化平台、科技公益性服务机构的定位,遵循共建、共治、共享原则,系统性打造开源开放框架,搭建国际开源社区,提升行业协作效率,赋能千行百业。此次新增捐赠人的公布,是对过去一段时间内,在开源领域做出突出贡献单位的认可与鼓励。
在全球开源趋势下,中国开源软件的发展正步入快车道。开源技术不仅引领了新时代开发者生产力的飞跃,更成为支撑数字经济、驱动科技创新的坚实底座。作为开源技术的坚定推进者和建设者,宝兰德多年来厚植开源,贡献开源,与国产CPU、操作系统、数据库、应用软件等上千家生态合作伙伴完成了产品兼容性互认证,构建我国自主的IT底层架构和标准,完善产业发展支撑环境。同时,宝兰德作为CCSA、CESA、ITSS、NITS等国内核心标准组成员,广泛参与行业项标准的制定和推广,为构建健康,活跃的开源生态贡献积极力量。
作为openEuler项目群的青铜捐赠人,宝兰德将积极参与openEuler社区作为重要发展战略,首批通过openEuler操作系统适配认证,以及openGauss、MindSpore、Cangjie等开源项目的共建共创,基于毕昇JDK推出了商业版天工JDK,与相关方基于国家高质量专项共同推进openEuler系商业化落地。未来,宝兰德将进一步参与社区云原生、编译器、JDK、优化和AI相关SIG工作,并致力于将产品技术与行业属性深度耦合,为电信、金融、政府、能源、交通、教育等关键领域提供稳定可靠的解决方案和服务。
在持续贡献openEuler开源社区的同时,宝兰德将与开放原子开源基金会一起,携手产业链上下游伙伴,从社区运营、技术支撑、人才培养等各方面,积极发挥开源产业链核心企业引领作用,进一步探索我国开源生态的创新发展模式,推动中国开源生态健康有序、高质量发展,推动我国从开源大国向开源强国迈进。
相关文章:

宝兰德荣获openEuler项目群青铜捐赠人称号,共筑开源生态繁荣新篇章
近日,开放原子开源基金会正式公布了新增捐赠人名单,宝兰德凭借在开源领域的卓越贡献与深厚实力,被授予openEuler项目群青铜捐赠人称号。 开放原子开源基金会是致力于推动全球开源事业发展的非营利机构,于2020年6月在北京成立。开放…...

【Python单元测试】学习笔记3
文章目录 08.PyTest框架什么是PyTestPyTest的优点PyTest的测试环境PyTest常用参数跳过测试 09.PyTest fixture基础PyTest fixture定义和使用引用多个Fixture 10. conftest.pyconftest.py的用途 11. 参数化测试用例为什么需要参数化测试用例使用parameterizer插件实现使用pytest…...

OpenSSL源码编译及Debug
** 1. 环境 Linux 5.19.0-14-generic 22.04.1-Ubuntu 2. 所需工具 gcc version 11.3.0 (Ubuntu 11.3.0-1ubuntu1~22.04) cmake version 3.22.1 3. 步骤 3.1 获取openssl源码 方法可以git clone获得源码,或者直接去GitHub上下载压缩包,GitHub网址…...

go之goburrow/modbus 学习
goburrow/modbus 是一个用Go语言实现的Modbus协议库,提供了Modbus主机(Master)和从机(Slave)的实现,支持两种主要的Modbus传输模式:Modbus TCP和Modbus RTU。 功能介绍 1. 支持的传输模式 Mod…...

开放词汇目标检测(Open-Vocabulary Object Detection, OVOD)算法是什么?
开放词汇目标检测(Open-Vocabulary Object Detection, OVOD)算法是什么? 随着计算机视觉技术的快速发展,目标检测(Object Detection)已经在各种应用场景中得到了广泛的应用。然而,传统的目标检…...

【教程】Ubuntu给pycharm添加侧边栏快捷方式
转载请注明出处:小锋学长生活大爆炸[xfxuezhagn.cn] 如果本文帮助到了你,欢迎[点赞、收藏、关注]哦~ 以下教程不仅限于pycharm,其他软件也是一样操作 1、进入到pycharm的目录,先通过命令行打开pycharm: ./bin/pycharm…...

三个月外贸小白好迷茫,该何去何从?
最近看到一个共性的问题,也许对于大多数外贸新人来说,都有过这样的困扰和无力感,也许对于每一个没有强大背景的外贸小伙伴来说,可能都是这样一路成长起来的。 大家好,我是一名普通二本英专生,八月中旬入职…...
)
MySQL数据库——基本查询(Create)
CRUD:Create(创建)Retrieve(读取)Update(更新)Delete(删除) 1.Create ①单行数据全列插入 insert [into] table_name [(colume[,colume]……)] values (value_list) […...

spring-security-1-快速入门
1 功能 身份认证(authentication)授权(authorization)防御常见攻击 身份认证:常见账号密码登录,短信登录 授权:什么样的角色,能看见什么菜单,能访问哪些接口。 2 pom <dependency><groupId>org.springf…...

5 大场景上手通义灵码企业知识库 RAG
大家好,我是通义灵码,你的智能编程助手!最近我又升级啦,智能问答功能全面升级至 Qwen2,新版本在各个方面的性能和准确性都得到了显著提升。此外,行间代码补全效果也全面优化,多种编程语言生成性…...

免费远程控制电脑的软件有哪些?
什么是远程控制? 远程控制是一种通过网络从一台设备操作另一台设备的技术。连接后,用户可以直接远程操作那台电脑进行各种操作。随着科技的不断进步和用户需求的增加,远程控制市场日益蓬勃。远程控制不仅应用于远程办公和远程教学࿰…...

Linux软件包yum
目录 Linux软件包管理器 yum关于rzsz注意事项查看软件包如何安装软件卸载命令 Linux开发工具Linux编辑器-vim使用1. vim的基本概念2. vim的基本操作3. vim正常模式命令集4. vim末行模式命令集5. vim操作总结 小彩蛋 Linux软件包管理器 yum 软件包 在Linux下安装软件ÿ…...

网页的切换与嵌套
网页的切换与嵌套 网页的切换 在浏览器窗口中如果点击超链接标签会在当前的浏览器窗口中显示新的数据,但有些超链接标签点击后却会在一个新的窗口显示数据,这种情况下就无法对新的开的窗口页面进行操作了。 基于这种情况,我们就需要使用dri…...
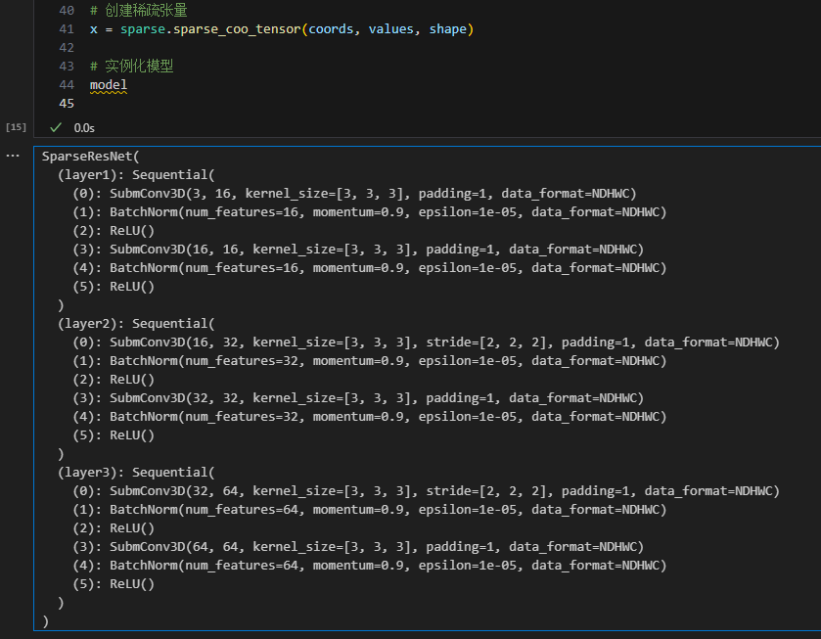
基于飞桨框架的稀疏计算使用指南
本文作者-是 Yu 欸,华科在读博士生,定期记录并分享所学知识,博客关注者5w。本文将详细介绍如何在 PaddlePaddle 中利用稀疏计算应用稀疏 ResNet,涵盖稀疏数据格式的础知识、如何创建和操作稀疏张量,以及如何开发和训练…...

启明云端WT32C3-S6物联网模块,乐鑫ESP32-C3芯片技术应用
随着物联网技术的飞速发展,智能设备在我们生活中的应用越来越广泛。从智能电网到远程医疗,从楼宇自动化到智能家居,这些技术正在改变我们的生活方式。 在这样的背景下,启明云端推出的WT32C3-S6 WiFi模块以其低功耗、高性价比的特…...

超越流水线,企业研发规范落地新思路
作者:子丑 内容大纲: 1、研发规范≠流程约束 2、自动化工具→研发规范载体 3、研发规范在工具上的落地示例 4、研发规范的选型方法与常见实践 研发规范≠流程约束 这个故事特别适合研发规范的场景,我们要避免成为把猫绑在柱子上的信众…...

财务会计与管理会计(四)
文章目录 月度数据统计分析OFFSET函数在图表分析中的应用 多种费用组合分析图SUMPRODUCT函数 省公司全年数据分析模板INDIRECT、OFFSET函数 多公司分季度数据筛选VLOOKUP、IFERROR函数的应用 淘宝后台数据分析OFFSET函数在跨表取数中的应用 燃气消耗台账数据统计分析图SUMPRODU…...
回归分析系列1-多元线性回归
03 多元线性回归 3.1 简介 多元线性回归是简单线性回归的扩展,允许我们同时研究多个自变量对因变量的影响。多元回归模型可以表示为: 其中,x1,x2,…,xp是 p 个自变量,β0 是截距,β1,β2,…,βp是对应的回归系数&…...

web小游戏开发:拼图——蜂巢拼图
web小游戏开发:拼图——蜂巢拼图 蜂巢拼图游戏规则调整选项切图计算六边形的宽和高铺上背景画出蜂巢制作图块游戏方法打乱排列拖拽图块开始拖拽拖拽移动放置图块小结蜂巢拼图 之前我们已经完成了长方形的拼图代码,包括了三个游戏方式,并讨论了带咬合齿的游戏代码该如何制作…...

springCloud集成activiti5.22.0流程引擎(分支)
springCloud集成activiti5.22.0流程引擎 点关注不迷路,欢迎再访! 精简博客内容,尽量已行业术语来分享。 努力做到对每一位认可自己的读者负责。 帮助别人的同时更是丰富自己的良机。 文章目录 springCloud集成activiti5.22.0流程引擎一.Sprin…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...
