Java之动态规划之子序列问题
目录
0.动态规划问题
一.最长递增子序列
1.题目描述
2.问题分析
3.代码实现
二.最长递增子序列
1.题目描述
2.问题分析
3.代码实现
三.最长重复子数组
1.题目描述
2.问题分析
3.代码实现
4.代码的优化(滚动数组)
四.最长公共子序列
1.题目描述
2.问题分析
3.代码实现
4.代码优化(滚动数组)
五.不相交的线
1.题目描述
2.问题分析
3.代码实现
4.代码优化(滚动数组)
六.最大子数组和
1.题目描述
2.问题分析
3.代码实现
七.判断子序列
1.题目描述
2.问题分析
3.代码实现
4.双指针代码实现
0.动态规划问题
动态规划(Dynamic Programming)算法的核心思想是:将大问题划分为小问题,进行解决,从而一步步获取最优解的处理算法
动态规划对于解决最优子结构啊和重叠子问题等问题时候,有着很好的应用
对于动态规划问题,大致可以分为以下几步:
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
一.最长递增子序列
1.题目描述
给你一个整数数组
nums,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,
[3,6,2,7]是数组[0,3,1,6,2,2,7]的子序列。
力扣:力扣
2.问题分析
这一题首先要理解子序列问题,子序列不一定是连续一段的数组(子数组),只需要它的序列是递增的即可(例如index=0,2,3)
对于解决这样的动态规划的背包问题,还是采用通用的五个步骤
1.确定dp数组(dp table)以及下标的含义
本题的dp数组定义不是根据题目直接来进行定义,需要根据题意进行变通定义
dp[i]数组的含义:以nums[i]为结尾的最长递增子序列长度为dp[i]
注意:这里一定要以nums[i]为结尾,不可去除这个元素
2.确定递推公式
位置i的元素最长的递增子序列等于位置从0到j-1位置上最长递增子序列+1的最大值
递推公式:if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
注意:这里dp[i] = max(dp[i], dp[j] + 1)是为了取dp[i]的最大值,并不是dp[i]和dp[j] + 1比较
注意:这里它的最大值并不一定出现在dp[nums.length-1]的位置,如何最后一个数字比前边的都小,而dp数组的定义必须以nums[i]为结尾,所有此时dp[i]的值可能为1,因为应该取dp数组元素的最大值
3.dp数组如何初始化
由题意可知,无论前边的nums[j]是否比nums[i]大,总有一个元素满足递增序列,就是它本身自己,所有每一个dp[i]都应该初始化为1
4.确定遍历顺序
因为最长递增子序列是从前到后递增,所以我们也应该从左到右进行遍历
5.举例推导dp数组
对nums = [10,9,2,5,3,7,101,18]进行推导
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| dp[i] | 1 | 1 | 1 | 2 | 2 | 3 | 4 | 4 |
它的最长的递增序列是{2,3,7,101}或者{2,3,7,18}
3.代码实现
public int lengthOfLIS(int[] nums) {int[] dp = new int[nums.length];int max = 1;Arrays.fill(dp, 1);for (int i = 1; i < nums.length; ++i) {for (int j = 0; j < i; ++j) {if (nums[i] > nums[j])dp[i] = Math.max(dp[i], dp[j] + 1);}max = Math.max(max, dp[i]);}return max;}二.最长递增子序列
1.题目描述
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标
l和r(l < r)确定,如果对于每个l <= i < r,都有nums[i] < nums[i + 1],那么子序列[nums[l], nums[l + 1], ..., nums[r - 1], nums[r]]就是连续递增子序列。
力扣:力扣
2.问题分析
这里明确说了是连续的子序列,所以序列值应该是连在一起的,如:index=1,2,3
对于解决这样的动态规划的背包问题,还是采用通用的五个步骤
1.确定dp数组(dp table)以及下标的含义
dp[i]数组的含义是:以nums[i]为结尾的连续递增子序列的最大值
2.确定递推公式
这一题和上一题明显的不同就是连续与否,上一题如何nums[i]<nums[i-1],那么它的递增还有可能和i-1之前的数据构成递增序列,这一题,因为存在一个连续,所以如果nums[i]<nums[i-1],那么他肯定是不能构成连续递增序列了,因此这时dp[i]=1;如果nums[i]>nums[i-1],说明与前边的元素构成连续递增序列,因此dp[i]=dp[i-1]+1;
递推公式为:if (nums[i] > nums[i - 1]) dp[i] = dp[i - 1] + 1;
注意:这一题仍然需要dp数组中的最大值,原因和上一题一样
3.dp数组如何初始化
和上一题一样,所有的初始化为1
4.确定遍历顺序
和上一题一样,从左到右,但这一题只需要一层循环
5.举例推导dp数组
推导nums = [1,3,5,4,7]
| i | 0 | 1 | 2 | 3 | 4 |
| dp[i] | 1 | 2 | 3 | 1 | 2 |
最长连续递增序列为:{1,3,5}
3.代码实现
public static int findLengthOfLCIS(int[] nums) {int[] dp = new int[nums.length];int max = 0;Arrays.fill(dp, 1);for (int i = 1; i < nums.length; ++i) {if (nums[i] > nums[i - 1])dp[i] = dp[i - 1] + 1;max = Math.max(i, dp[i]);}return max;}三.最长重复子数组
1.题目描述
给两个整数数组
nums1和nums2,返回 两个数组中 公共的 、长度最长的子数组的长度 。
力扣:力扣
2.问题分析
题目中说的就是子数组就是连续子序列
对于解决这样的动态规划的背包问题,还是采用通用的五个步骤
1.确定dp数组(dp table)以及下标的含义
因为这一题是两个数组,所以最好定义为二维数组
dp[i][j]的含义是:以nums1[i]结尾的A和以nums2[j]结尾的B,最长的公共子数组的长度是dp[i][j]
2.确定递推公式
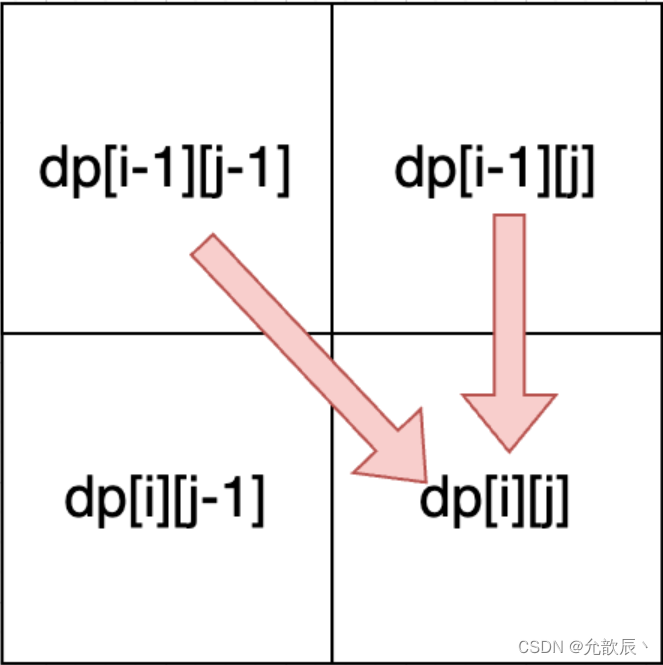
子数组和连续子序列的含义是一样的,如果nums1[i]==nums2[j],此时只需要知道前边的最长的公共子数组的最大长度,就是dp[i-1][j-1](含义是以nums1[i-1]结尾的A和以nums2[j-1]结尾的B,最长的公共子数组的长度),此时+1便等于dp[i][j],如果不相等的话,这个时候公共子数组长度显然为0,不需要赋值
所以递推公式为:if (nums1[i] == nums2[j]) dp[i][j] = dp[i - 1][j - 1] + 1;
注意:这一题仍然需要dp数组中的最大值,原因和上一题一样
3.dp数组如何初始化
由递推公式可以知道由斜上方的元素推导出来的,所以至少要对第一行和第一列进行初始化赋值

具体的初始化代码如下:
//对第一列进行初始化for (int i = 0; i < nums1.length; i++) {if (nums1[i] == nums2[0])dp[i][0] = 1;result = Math.max(result, dp[i][0]);}//对第一行进行初始化for (int j = 0; j < nums2.length; j++) {if (nums1[0] == nums2[j])dp[0][j] = 1;result = Math.max(result, dp[0][j]);}4.确定遍历顺序
由递推公式可以看出,是由从上到下,从左到右进行遍历的
5.举例推导dp数组
对nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]进行推倒后的dp数组
[0, 0, 1, 0, 0]
[0, 1, 0, 0, 0]
[1, 0, 0, 0, 0]
[0, 2, 0, 0, 0]
[0, 0, 3, 0, 0]
3.代码实现
public int findLength(int[] nums1, int[] nums2) {int[][] dp = new int[nums1.length][nums2.length];int result = 0;//对第一列进行初始化for (int i = 0; i < nums1.length; i++) {if (nums1[i] == nums2[0])dp[i][0] = 1;result = Math.max(result, dp[i][0]);}//对第一行进行初始化for (int j = 0; j < nums2.length; j++) {if (nums1[0] == nums2[j])dp[0][j] = 1;result = Math.max(result, dp[0][j]);}for (int i = 1; i < nums1.length; i++) {for (int j = 1; j < nums2.length; j++) {if (nums1[i] == nums2[j]) { // 防止 i-1 出现负数dp[i][j] = dp[i - 1][j - 1] + 1;}result = Math.max(result, dp[i][j]);}}return result;}
也可以进行这样设置 dp数组:以下标i - 1为结尾的A,和以下标j - 1为结尾的B,最长重复子数组长度为dp[i][j],这样的代码实现为 dp[i][0]和dp[0][j]没有意义,全部赋值为0 (推荐)
public int findLength(int[] nums1, int[] nums2) {int[][] dp = new int[nums1.length + 1][nums2.length + 1];int res = 0;for (int i = 1; i <= nums1.length; ++i) {for (int j = 1; j <= nums2.length; ++j) {if (nums1[i - 1] == nums2[j - 1])dp[i][j] = dp[i - 1][j - 1] + 1;res = Math.max(res, dp[i][j]);}}return res;}4.代码的优化(滚动数组)
这样其实和01背包的二维数组优化成滚动数组一个思路,都是长度为nums2.length长的数组,然后第一个从左到右遍历,第二个从右到左遍历,为了不影响其他数据使用成为第二次推导出的数据

01背包指路:Java之动态规划的背包问题_允歆辰丶的博客-CSDN博客
第一个dp数组的含义:以nums2[j]为结尾的dp[j]:代码实现
public int findLength4(int[] nums1, int[] nums2) {int[] dp = new int[nums2.length];int result = 0;//对第一行进行初始化for (int j = 0; j < nums2.length; j++) {if (nums1[0] == nums2[j])dp[j] = 1;result = Math.max(result, dp[j]);}System.out.println(Arrays.toString(dp));for (int i = 1; i < nums1.length; i++) {for (int j = nums2.length - 1; j >= 0; --j) {if (nums1[i] == nums2[j]) { // 防止 i-1 出现负数if (j == 0) {dp[j] = 1;continue;}dp[j] = dp[j - 1] + 1;result = Math.max(result, dp[j]);} else {dp[j] = 0;}}System.out.println(Arrays.toString(dp));}return result;}第二种dp数组的含义:以nums2[j-1]为结尾的dp[j]:代码实现(推荐)
public int findLength2(int[] nums1, int[] nums2) {int[] dp = new int[nums1.length + 1];int res = 0;for (int i = 1; i <= nums1.length; ++i) {for (int j = nums2.length; j >= 1; --j) {if (nums1[i - 1] == nums2[j - 1]) {dp[j] = dp[j - 1] + 1;} elsedp[j] = 0;res = Math.max(dp[j], res);}}return res;}四.最长公共子序列
1.题目描述
给定两个字符串
text1和text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回0。一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace"是"abcde"的子序列,但"aec"不是"abcde"的子序列。两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
力扣:力扣
2.问题分析
子序列,显然是不连续的
对于解决这样的动态规划的背包问题,还是采用通用的五个步骤
1.确定dp数组(dp table)以及下标的含义
dp[i][j]的含义:长度为[0,i-1]的text1和长度为[0,j-1]的text2最最长公共子序列的长度为dp[i][j]
注意:这里不一定一定以text[i-1]结尾,只需要在[0,i-1]任意子字符串最长即可
2.确定递推公式
主要就是两种情况,一种就是text1.charAt(i-1)==text2.charAt(j-1);另一种是不相同
当相等的情况,很显然就是两个字符串长度各-1的最长公共子序列的长度+1,就是 dp[i][j]=dp[i-1][j-1]+1 例如(aab和bab,dp[2][2]=1,dp[3][3]=2)
当不相等的时候,就是text1[0,i-2]的text2和长度为[0,j-1]和text1[0,i-1]的text2和长度为[0,j-2]的最大值作为dp[i][j]的值
dp[i][j]=max(dp[i][j-1],dp[i-1][j])
if (text1.charAt(i - 1) == text2.charAt(j - 1))dp[i][j] = dp[i - 1][j - 1] + 1;else {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);}3.dp数组如何初始化
因为dp[i][0]和dp[0][j]没有意义,所以初始化为0
,4.确定遍历顺序

由推导公式可以知道,遍历顺序是从左到右,从上到下的
5.举例推导dp数组
对于text1 = "abcde", text2 = "ace" 进行推导
[0, 0, 0, 0]
[0, 1, 1, 1]
[0, 1, 1, 1]
[0, 1, 2, 2]
[0, 1, 2, 2]
[0, 1, 2, 3]
最长公共子序列是 "ace" ,它的长度为 3 。
3.代码实现
public int longestCommonSubsequence(String text1, String text2) {int[][] dp = new int[text1.length() + 1][text2.length() + 1];for (int i = 1; i <= text1.length(); ++i) {for (int j = 1; j <= text2.length(); ++j) {if (text1.charAt(i - 1) == text2.charAt(j - 1))dp[i][j] = dp[i - 1][j - 1] + 1;else {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[text1.length()][text2.length()];}4.代码优化(滚动数组)
public int longestCommonSubsequence2(String text1, String text2) {int[] dp = new int[text2.length() + 1];for (int i = 1; i <= text1.length(); ++i) {int pre=dp[0];for (int j = 1; j <= text2.length(); ++j) {int cur = dp[j];if (text1.charAt(i - 1) == text2.charAt(j - 1))dp[j] = pre + 1;else {dp[j] = Math.max(cur, dp[j - 1]);}pre=cur;}}return dp[text2.length()];}五.不相交的线
1.题目描述
在两条独立的水平线上按给定的顺序写下
nums1和nums2中的整数。现在,可以绘制一些连接两个数字
nums1[i]和nums2[j]的直线,这些直线需要同时满足满足:
nums1[i] == nums2[j]- 且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
力扣:力扣
2.问题分析
这一题看样子题目意思改变了很多,其实和上一题字符串的意思是一样的,它规定是连线不可以相交的,其实意思就是i与j的相对位置是不可以改变的,比如nums1[i]==nums[j]了,那么这个时候你只能继续向后遍历,不可以反过来遍历,例如(nums1[i+1]==nums[j-1])这样是不行的,只能接着往后面相加,这样就和上一题的意思是一模一样的了
例如这一题:

5.举例推导dp数组
对于nums1 = [1,4,2], nums2 = [1,2,4]推导
[0, 1, 1, 1]
[0, 1, 1, 2]
[0, 1, 2, 2]
nums1[1]=4 到 nums2[2]=4,所以最多画两条线
3.代码实现
public int maxUncrossedLines(int[] nums1, int[] nums2) {int[][] dp = new int[nums1.length + 1][nums2.length + 1];for (int i = 1; i <= nums1.length; ++i) {for (int j = 1; j <= nums2.length; ++j) {if (nums1[i - 1] == nums2[j - 1])dp[i][j] = dp[i - 1][j - 1] + 1;else {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[nums1.length][nums2.length];}4.代码优化(滚动数组)
public static int maxUncrossedLines2(int[] nums1, int[] nums2) {int[] dp = new int[nums2.length + 1];for (int i = 1; i <= nums1.length; ++i) {int pre = dp[0];for (int j = 1; j <= nums2.length; ++j) {int cur = dp[j];if (nums1[i - 1] == nums2[j - 1])dp[j] = pre + 1;else {dp[j] = Math.max(cur, dp[j - 1]);}pre = cur;}}return dp[nums2.length];}六.最大子数组和
1.题目描述
给你一个整数数组
nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组 是数组中的一个连续部分。
力扣:力扣
2.问题分析
最大子数组说明是连续的
对于解决这样的动态规划的背包问题,还是采用通用的五个步骤
1.确定dp数组(dp table)以及下标的含义
dp[i]的含义是:以nums[i]结尾的子数组的最大和是dp[i]
2.确定递推公式
存在两种情况,一种就是i前边的最大子数组和加上nums[i],一种就是从只有nums[i],因为dp[i-1]可能存在已经是负值的情况,如果再加上nums[i],只会使值变小,这个时候从新从nums[i]开始更好,如果前边已经是正数了,加上nums[i](可能使dp[i-1]>dp[i],因为nums[i]可能为负数,因为dp数组定义的缘故,必须加入)
所以递推公式为:dp[i]=max(dp[i-1]+nums[i],nums[i]);
3.dp数组如何初始化
由递推公式可知,只需要初始化dp[0],因为子数组至少有一个值,所以dp[0]=nums[0];
4.确定遍历顺序
由递推公式可知,从左到右进行遍历
5.举例推导dp数组
对[-2,1,-3,4,-1,2,1,-5,4]进行推导
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dp[i] | -2 | 1 | -2 | 4 | 3 | 5 | 6 | 1 | 5 |
3.代码实现
public int maxSubArray(int[] nums) {int[] dp = new int[nums.length];int res=nums[0];dp[0] = nums[0];for (int i = 1; i < nums.length; ++i) {dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);res=Math.max(res,dp[i]);}return res;}七.判断子序列
1.题目描述
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,
"ace"是"abcde"的一个子序列,而"aec"不是)。
力扣:力扣
2.问题分析
子序列:是不连续的问题,这一题其实和四.最长公共子序列差不多的问题,略有不同之后说明
对于解决这样的动态规划的背包问题,还是采用通用的五个步骤
1.确定dp数组(dp table)以及下标的含义
dp[i][j]的含义是:从[0,i-1]的子字符串s和从[0,j-1]的子字符串t,相同子序列的长度是dp[i][j]
注意:这里和第四题的dp数组还是有一点区别的
2.确定递推公式
主要也是分为两种情况,一种就是当s.charAt[i-1]==t.charAt[j-1],这个时候dp[i][j] = dp[i - 1][j - 1] + 1.这个时候相当于在i位置上的字符在t中找了 第二种情况:s.charAt[i-1]!=t.charAt[j-1],这个时候就不能和第四题一样了,因为这一题是要找s是否为 t 的子序列,s数组如果你找到了几个字符在t中,你这个时候是不可以dp[i-1][j],这样就是s向前找,但是s还不可以删除的,例如s="abc"c,t="aacbc",这个时候第一个a==a,然后b!=a,但这个时候你不可以使s字符串找到前边的a.
所以推导公式为:
if (s.charAt(i - 1) == t.charAt(j - 1))dp[i][j] = dp[i - 1][j - 1] + 1;
else {dp[i][j] = dp[i][j - 1];
}3.dp数组如何初始化
由递推公式可知,dp[0][j]和dp[i][0]没有意义,初始化为0
4.确定遍历顺序
由递推公式可知,从前到后,从上到下
5.举例推导dp数组
对s = "abc", t = "ahbgdc"进行推导
[0, 1, 1, 1, 1, 1, 1]
[0, 0, 0, 2, 2, 2, 2]
[0, 0, 0, 0, 0, 0, 3]
3.代码实现
public boolean isSubsequence(String s, String t) {int[][] dp = new int[s.length() + 1][t.length() + 1];for (int i = 1; i <= s.length(); ++i) {for (int j = 1; j <= t.length(); ++j) {if (s.charAt(i - 1) == t.charAt(j - 1))dp[i][j] = dp[i - 1][j - 1] + 1;else {dp[i][j] = dp[i][j - 1];}}}return dp[s.length()][t.length()]==s.length();}4.双指针代码实现
当然,这一题也可以选择使用双指针来解决,代码实现
public boolean isSubsequence2(String s, String t) {int j = 0;for (int i = 0; i < s.length(); ++i) {while (j < t.length() && s.charAt(i) != t.charAt(j)) {j++;}j++;}return j <= t.length();}八.不同的子序列
1.题目描述
给定一个字符串
s和一个字符串t,计算在s的子序列中t出现的个数。字符串的一个 子序列 是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新字符串。(例如,
"ACE"是"ABCDE"的一个子序列,而"AEC"不是)题目数据保证答案符合 32 位带符号整数范围。
力扣:力扣
2.问题分析
这里和第七题有相似之处,但还是有一定的区别
对于解决这样的动态规划的背包问题,还是采用通用的五个步骤
1.确定dp数组(dp table)以及下标的含义
dp[i][j]的含义是:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]
2.确定递推公式
其实这一题和上一题一样,dp[i][j]还是分两种情况
一种:当s.charAt[i-1]==t.charAt[j-1],此时dp[i][j]由两部分组成
当t.charAt[j-1]来进行匹配出现次数的时候,这一部分为dp[i-1][j-1]
当t.charAt[j-1]不是匹配出现次数的时候,这一部分为dp[i-1][j]
另一种:当s.charAt[i-1]!=t.charAt[j-1],这个时候只有t.charAt[j-1]不是匹配出现次数的时候为dp[i-1][j]
if (s.charAt(i - 1) == t.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];} else {dp[i][j] = dp[i - 1][j];}
3.dp数组如何初始化
首先我们需要先回顾一下dp数组的含义
dp[i][0]的含义是t数组为空的时候,以i-1结尾的s出现在t中的个数,因为t为空,这个时候赋值为1
dp[0][j]的含义是s数组为空,s出现在以j-1结尾的t中的个数,这个时候赋值为0
for (int i = 0; i <= s.length(); ++i) {dp[i][0] = 1;}4.确定遍历顺序
由递推公式可知,从前到后,从上到下
5.举例推导dp数组
对s = "rabbbit", t = "rabbit"进行推导
[1, 0, 0, 0, 0, 0, 0]
[1, 1, 0, 0, 0, 0, 0]
[1, 1, 1, 0, 0, 0, 0]
[1, 1, 1, 1, 0, 0, 0]
[1, 1, 1, 2, 1, 0, 0]
[1, 1, 1, 3, 3, 0, 0]
[1, 1, 1, 3, 3, 3, 0]
[1, 1, 1, 3, 3, 3, 3]
3.代码实现
public int numDistinct(String s, String t) {int[][] dp = new int[s.length() + 1][t.length() + 1];for (int i = 0; i <= s.length(); ++i) {dp[i][0] = 1;}for (int i = 1; i <= s.length(); ++i) {for (int j = 1; j <= t.length(); ++j) {if (s.charAt(i - 1) == t.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];} else {dp[i][j] = dp[i - 1][j];}}}return dp[s.length()][t.length()];}相关文章:

Java之动态规划之子序列问题
目录 0.动态规划问题 一.最长递增子序列 1.题目描述 2.问题分析 3.代码实现 二.最长递增子序列 1.题目描述 2.问题分析 3.代码实现 三.最长重复子数组 1.题目描述 2.问题分析 3.代码实现 4.代码的优化(滚动数组) 四.最长公共子序列 1.题目描述 2.问题分析 3.代…...

java ArrayList
目录 一.简单介绍 二.ArrayList的底层结构 2.1ArrayList的底层结构和操作分析 2.ArrayList 底层源码分析 三.ArrayList 方法 四.代码使用方法 一.简单介绍 ArrayList 类是一个可以动态修改的数组,与普通数组的区别就是它是没有固定大小的限制,我们…...

前端——周总结系列四
1 JS变量与常量 概述 变量:在后续编码过程中会被重新赋值,是不断变化的。常量:固定不变的数据,日常生活比如性别男,代码层面是在编码过程中不会变化的固定数据。 命名规则 变量 可以包含数字,字母&…...
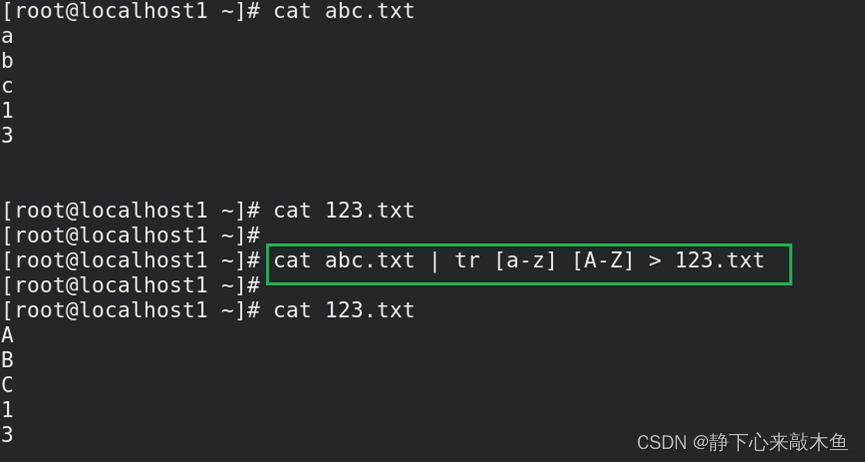
Linux重定向符、管道符讲解
目录 重定向 将命令与文件进行互动 输出重定向 输入重定向 管道符 将命令与命令互动起来 重定向 将命令与文件进行互动 重定向分类 一般情况下,Linux命令运行时都会打开一下三个文件 标准输入文件:stdin文件,文件描述符为0,Li…...
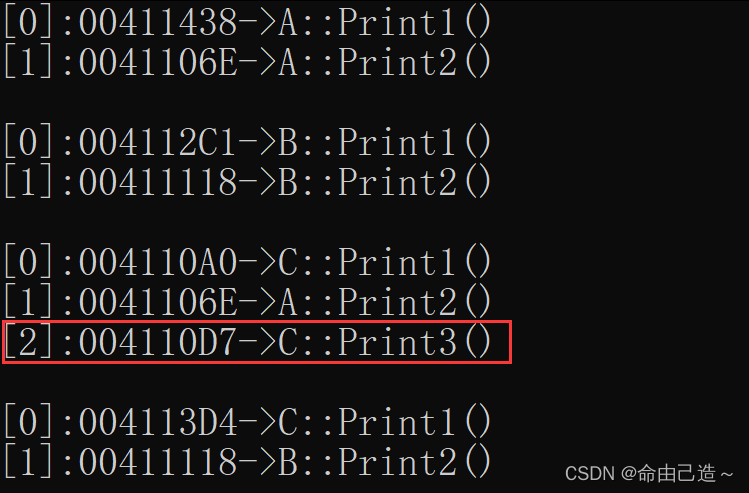
【C++】多态
多态一、多态的概念及定义1.1 虚函数1.2 虚函数重写的特殊情况1.3 override 和 final二、抽象类2.1 概念2.2 用处三、多态的原理3.1 虚函数表3.1.1 虚函数与虚表的位置3.2 多态的原理3.3 静态绑定和动态绑定四、单/多继承的虚函数表4.1 单继承的虚函数表4.2 多继承的虚函数表一…...

分布式项目-品牌管理(5、6)
【今日成果】: //使用阿里云OSS服务: //使用v-if如果地址没有就不显示 , 如果地址错误图片就显示不出来; 【快速回顾】: 任何数据的删除都不要使用物理上的删除,应当使用逻辑上的删除!&…...
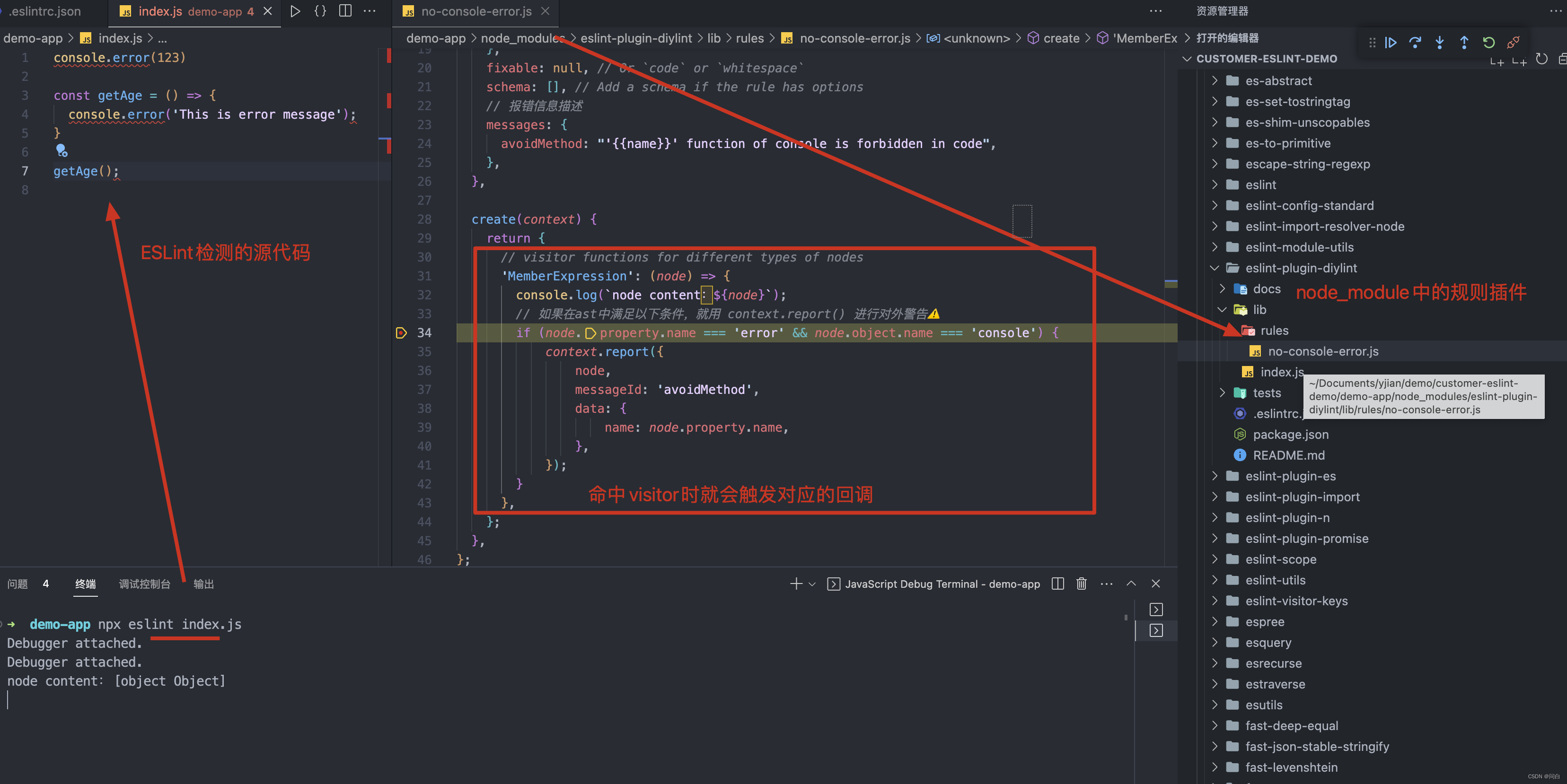
自定义ESLint规则开发与使用
自定义eslint及使用 项目结构 |-eslint-plugin-demo //自定义eslint插件项目 | |-demo-app // 使用自定义eslint的测试应用 |-README.md 项目效果: github项目地址 自定义ESLint环境准备 安装脚手架 执行下列命令来安装开发eslint的脚手架。 yo(y…...

【JavaScript】35_包装类与垃圾回收机制
10、包装类 在JS中,除了直接创建原始值外,也可以创建原始值的对象 通过 new String() 可以创建String类型的对象 通过 new Number() 可以创建Number类型的对象 通过 new Boolean() 可以创建Boolean类型的对象 但是千万不要这么做 包装类࿱…...

【CS224W】(task3)NetworkX工具包实践
note 节点可以为任意可哈希的对象,比如字符串、图像、XML对象,甚至另一个Graph、自定义的节点对象。通过这种方式可以自由灵活地构建:图为节点、文件为节点、函数为节点,等灵活的图形式。暂时省略:【B5】计算机网络图…...
ansible的模块详解
ansible 的概述 什么是ansible Ansible是一款为类Unix系统开发的自由开源的配置和自动化工具。 它用Python写成,类似于saltstack和Puppet,但是有一个不同和优点是我们不需要在节点中安装任何客户端。 它使用SSH来和节点进行通信。Ansible基于 Python…...

《Terraform 101 从入门到实践》 Functions函数
《Terraform 101 从入门到实践》这本小册在南瓜慢说官方网站和GitHub两个地方同步更新,书中的示例代码也是放在GitHub上,方便大家参考查看。 Terraform的函数 Terraform为了让大家在表达式上可以更加灵活方便地进行计算,提供了大量的内置函数…...

使用kubeadm快速部署一个K8s集群
wkubeadm是官方社区推出的一个用于快速部署kubernetes集群的工具。 这个工具能通过两条指令完成一个kubernetes集群的部署: # 创建一个 Master 节点 $ kubeadm init# 将一个 Node 节点加入到当前集群中 $ kubeadm join <Master节点的IP和端口 >1. 安装要求 …...

初探富文本之CRDT协同算法
初探富文本之CRDT协同算法 CRDT的英文全称是Conflict-free Replicated Data Type,最初是由协同文本编辑和移动计算而发展的,现在还被用作在线聊天系统、音频分发平台等等。当前CRDT算法在富文本编辑器领域的协同依旧是典型的场景,常用于作为…...
Dubbo和Zookeeper集成分布式系统快速入门
文件结构 代码部分 1、新建provider-server导入pom依赖 <dependency><groupId>org.apache.dubbo</groupId><artifactId>dubbo-spring-boot-starter</artifactId><version>2.7.3</version></dependency><dependency>&l…...
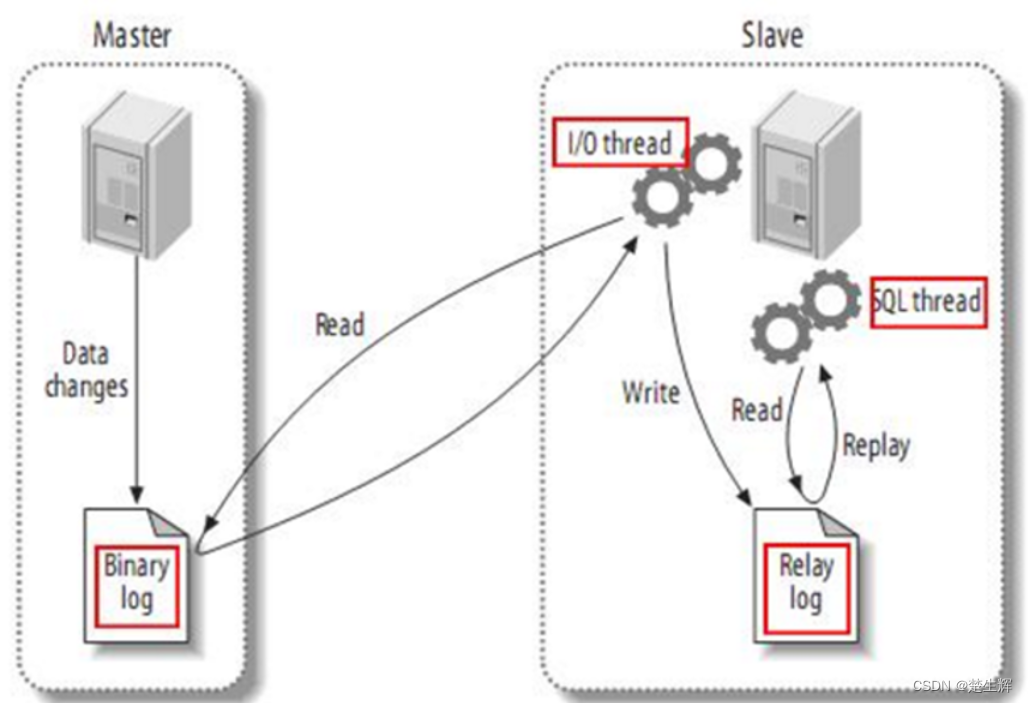
大数据工具Maxwell的使用
1.Maxwell简介 Maxwell 是由美国Zendesk公司开源,用Java编写的MySQL变更数据抓取软件。它会实时监控Mysql数据库的数据变更操作(包括insert、update、delete),并将变更数据以 JSON 格式发送给 Kafka、Kinesi等流数据处理平台。 官…...

freesurfer如何将组模板投影到个体空间——如投影 Schaefer2018 到个体空间
freesurfer如何将组模板投影到个体空间——如投影 Schaefer2018 到个体空间 freesurfer如何将组模板投影到个体空间? freesurfer如何将组模板投影到个体空间——如投影 Schaefer2018 到个体空间freesurfer的整理流程freesurfer的安装freesurfer对结构像分割流程及批处理代码fr…...
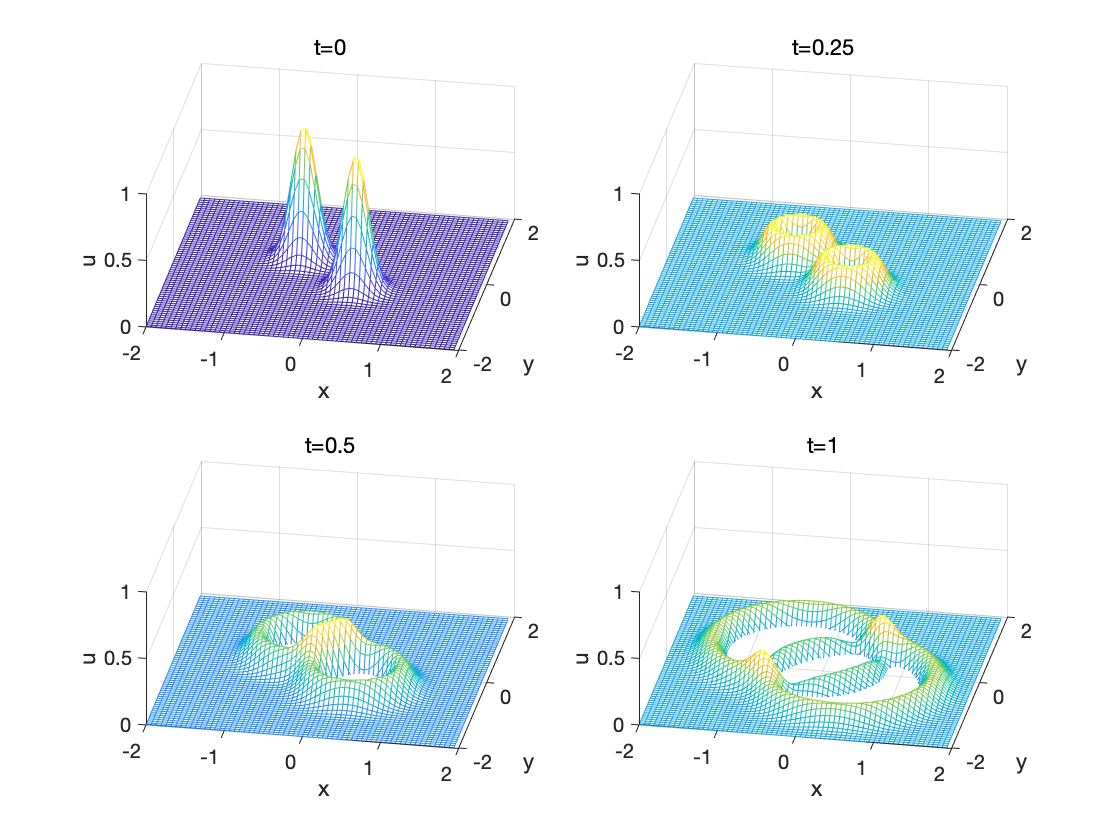
Matlab傅里叶谱方法求解二维波动方程
傅里叶谱方法求解基本偏微分方程—二维波动方程 二维波动方程 将一维波动方程中的一维无界弦自由振动方程推广到二维空间上, 就得到了描述无界 (−∞<x,y<∞)(-\infty<x, y<\infty)(−∞<x,y<∞) 弹性薄膜的波动方程: ∂2u∂t2a2(∂2∂x2∂2∂y2)u(1)\frac…...

【深度学习】卷积神经网络
1 卷积神经网络(CNN)可以做什么? 检测任务分类与检索超分辨率重构:将图像训练的更清晰医学任务等无人驾驶人脸识别 2 用GPU:图像处理单元 比CPU块一百倍以上 3 卷积神经网络与传统神经网络的区别 传统神经网络&…...
【C++】六个默认成员函数——取地址重载,const成员函数
🍅 初始化和清理 拷贝复制 目录 ☃️1.取地址重载 ☃️2.const取地址操作符重载 这两个运算符一般不需要重载,使用编译器生成的默认取地址的重载即可,只有特殊情况,才需要重载,比如想让别人获取到指定的内容…...
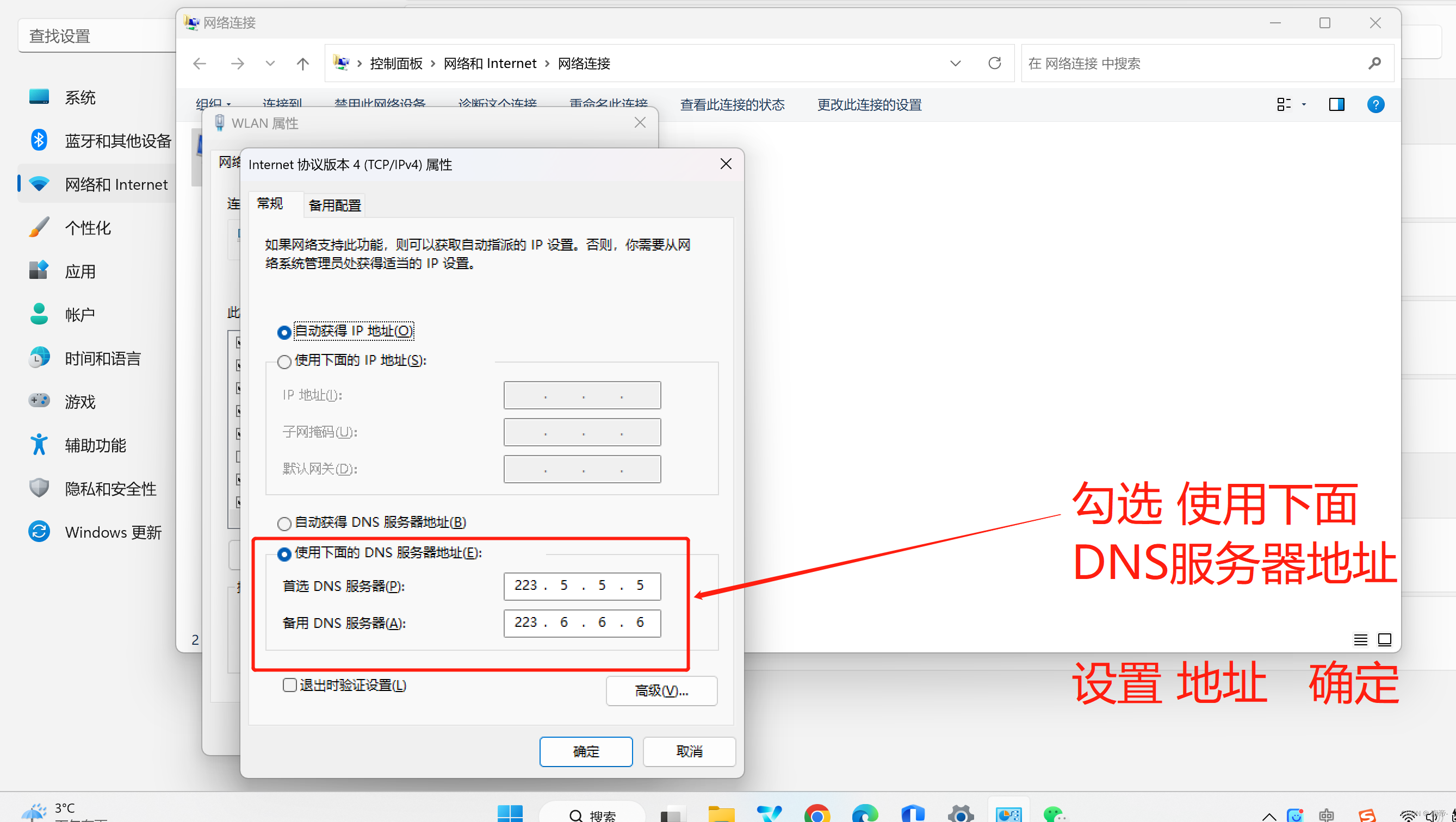
Win11浏览器无法上网,秒杀网上99.9%教程—亲测完胜
前言 例如:网上的教程 列如: 关闭代理服务器、QQ微信可以登录,但浏览器无法上网、Win11、Win10无法上网、重启网络、重启电脑、去掉代理服务器等等。 一系列教程,要多鸡肋就多鸡肋。 我是用我2020年在CSDN上发布的第一篇文章&…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

Qt Quick Controls模块功能及架构
Qt Quick Controls是Qt Quick的一个附加模块,提供了一套用于构建完整用户界面的UI控件。在Qt 6.0中,这个模块经历了重大重构和改进。 一、主要功能和特点 1. 架构重构 完全重写了底层架构,与Qt Quick更紧密集成 移除了对Qt Widgets的依赖&…...

短视频时长预估算法调研
weighted LR o d d s T p 1 − p ( 1 − p ) o d d s T p ( T p o d d s ∗ p ) o d d s p o d d s T o d d s odds \frac{Tp}{1-p} \newline (1-p)odds Tp \newline (Tp odds * p) odds \newline p \frac{odds}{T odds} \newline odds1−pTp(1−p)oddsTp(Tpodds…...

AIGC 基础篇 Python基础 02
1.bool类型 书接上回,我们上次最后讲了三大数据类型,除了这三个之外,Python也有bool类型,也就是True和False。 a 2 print(a1) print(a2) 像这里,输出的内容第一个是False,因为a的值为2,而第…...
