数学建模预测类—【一元线性回归】
每日格言:行动是治愈恐惧的良药,而犹豫拖延将不断滋养恐惧.
目录
前言
一、什么是回归分析?
1.概念理解
2.分类和一般步骤
二、一元线性回归(Matlab算法)
1.利用regress函数
2、例题讲解
总结
前言
在具体讲述线性回归的有关算法和解题思路时,我们会先讲一些有关回归分析的基础(建议大家可以看一下,理解一下原理)已经懂了的友友可以直接跳过~😏🙌
一、什么是回归分析?
1.概念理解
在统计学中,回归分析(regression analysis)指的是确定两种或两种以上变量间相互依赖的定量关
系的一种统计分析方法。
在大数据分析中,回归分析是一种预测性的建模技术,它研究的是因变量(目标)和自变量(预测器)之间的关系。
总而言之,回归分析通常用于预测分析以及发现变量之间的因果关系(通俗来讲就是🤔:根据已有数据验证自变量和因变量之间的某种函数关系是正确的)
2.分类和一般步骤
- 回归分析有两种分类方式:
根据变量的数目可以分为一元回归、多元回归
根据自变量与因变量的表现形式,分为线性和非线性
根据排列组合(2X2)也就是回归分析包括四个方向:
①一元线性回归分析、②多元线性回归分析、③一元非线性回归分析、④多元非线性回归分析
- 回归分析的一般步骤

简要总结一下这张图就是:找到自变量(x)和因变量(y)建立回归方程,然后验证方程的可行性,最后再根据回归方程进行预测.下面我们用一元线性回归方程的例子具体讲一下整个过程
问题:人均收入是否会显著影响人均食品消费支出?
- 确定解释变量(x)和被解释变量(y)
已知人均收入——x,人均食品消费支出——y
- 确定回归模型建立回归方程
根据我们的常识我们可知,人均收入应该是和人均食品消费成正比,这里只涉及一个自变量,则一元线性回归模型可表示为:
𝑦 = 𝛽0 + 𝛽1x + 𝜖(误差)(😶🌫️这里如何求相应的参数后面我们会细讲,这里就是了解一下流程~🫡)
- 检验(不同的回归模型检验方法不同,这里就提一些会用到的指标)
我们通常使用以下几个标准来度量回归方程的可靠性(我们只要会用即可):
- 估计标准误差越小,则数据点围绕回归直线的分散程度越小,回归方程的代表性越大,可靠性越高
- 置信区间反映了参数估计的不确定性,如果一个参数的置信区间不包含零(对于斜率参数),则可以认为该参数对因变量有显著的影响。
- 而预测区间反映了预测值的不确定性,可以告诉我们预测值的可信度范围。
- 判定系数(R^2):R^2越趋近于1,我们方程的拟合程度越好
- 线性关系检验:计算检验统计量F,若𝐹 > 𝐹1−𝛼(1, 𝑛 − 2)(查表可得),拒绝𝐻0,否则接受𝐻0;(𝐻0(原假设):𝛽1 = 0,回归系数与0无显著差异,𝑦与x的线性关系不显著),所以拒绝H0说明y与x存在线性关系
- 回归系数的显著性检验:检验回归系数𝛽的值与0是否有显著性差异,若𝛽 ≠ 0,说明变量𝑌与𝑋之间存在显著的线性关系
- 通过构造t统计量并计算p值,如果p值小于预设的显著性水平(例如0.05),则认为参数是显著的。
- 预测
将所求回归方程和参数代入求解即可
二、一元线性回归(Matlab算法)
1.利用regress函数
𝑦 = 𝛽0 + 𝛽1x + 𝜖(误差)(一元线性回归方程模型)
1、输入变量:这里Y,X都是由样本数据构成的列向量;alpha——显著性水平,默认为0.05 ,一般不需要我们输入
2、输出变量:
𝑏— — 回归系数(β0,β1,···)
𝑏𝑖n𝑡— — 回归系数的区间估计
𝑟— — 残差
𝑟𝑖n𝑡— — 置信区间
stats— — 用于检验回归模型的统计量
stats有四个数值:决定系数R^2、𝐹值、与𝐹对应的概率𝑃、无偏估计𝜎^2
2、例题讲解

让我们预测身高为170的女生腿长可能为多少呢?
%一元线性回归
clear,clc
%1.输入数据
%输入X的样本值
x = [143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]';
%插入β0对应列
X = [ones(16,1),x];
%输入Y的样本值
Y = [88,85,88,91,92,93,93,95,96,98,97,96,98,99,100,102]';%2、回归分析及检验:
[b,bint,r,rint,stats]=regress(Y,X);
%输出我们需要的数据
% β0=-16.0730,置信区间为[-33.7071,1.5612]
% β1=0.7194,置信区间为[0.6047,0.8340]
% R^2=0.9282 F=180.9531 p=0.0000 1.7437
%p就是接受回归模型的风险,即犯错的概率
% 由p<0.05,可知回归模型y=-16.0730+0.7194x 成立%3、残差分析,作残差图
figure
rcoplot(r,rint);
%第二个值可视为异常值%4、预测及作图
figure
y = b(1)+b(2)*x;
%比较真实值与估计值所作图像
plot(x,Y,'b+',x,y,'r');这里我们作图后的图像大致为

由上图说明我们回归方程的建立是比较好的。
总结
完结撒花🎆🎆🎇🎇
通过本篇文章,我们深入探讨了回归分析中的关键概念,包括如何评估模型的拟合度、参数的显著性检验以及如何利用置信区间和预测区间进行预测分析。如果大家有任何疑问或需要进一步的帮助,请随时留言!
相关文章:

数学建模预测类—【一元线性回归】
每日格言:行动是治愈恐惧的良药,而犹豫拖延将不断滋养恐惧. 目录 前言 一、什么是回归分析? 1.概念理解 2.分类和一般步骤 二、一元线性回归(Matlab算法) 1.利用regress函数 2、例题讲解 总结 前言 在具体讲述线性回归…...

配置更加美观的 Swagger UI
//注册Swagger服务 private static void AddSwaggerService(IServiceCollection services){services.AddSwaggerGen(opt >{opt.SwaggerDoc("Push", new OpenApiInfo{Version "v1",Title "Push API",Description "Push API 文档"…...
)
软件测试 - 基础(软件测试的生命周期、测试报告、bug的级别、与开发人员产生争执的调解方式)
一、软件测试的生命周期 测试贯穿软件的整个生命周期 软件测试的生命周期: 需求分析 →测试计划→ 测试设计、测试开发→ 测试执行→ 测试评估->上线->运行维护 需求分析:判断用户的需求是否合理,是否可实现 测试计划:计划项…...

RTX 4070 GDDR6显存曝光:性能与成本的平衡之选
近期,关于NVIDIA RTX 4070新显卡的信息曝光,这款显卡将配备较为缓慢的GDDR6显存,而非更高性能的GDDR6X。这一配置的选择引发了业内的广泛关注,特别是在性能与成本的平衡问题上。 新版RTX 4070 OC 2X的核心特点 **1.显存类型与带…...

canvas的基础使用
canvas的基础使用 一、画一条直线二、线的属性设置三、防止多次绘制的样式污染四、闭合五、快捷绘制矩形六、绘制圆形七、绘制文字八、绘制图片js版dom版图片截取 一、画一条直线 画一条直线需要用到三个方法:cxt.moveTo、cxt.lineTo、cxt.stroke <canvas id&qu…...

Windows 常用网络命令之 telnet(测试端口是否连通)
文章目录 1 概述1.1 启用 telnet 2 常用命令2.1 ping:测试网络是否连通2.2 telnet:测试端口是否连通 3 扩展3.1 进入 cmd 命令3.2 cls 清屏命令 1 概述 1.1 启用 telnet telnet ip:port // 格式 telnet 10.0.24.154:8001若出现上述提示&…...

x264 编码器像素运算系列:asd8函数
x264 编码器中像素间运算 在 x264 编码器中有多种像素间的运算,如下: sad 计算:SAD(Sum of Absolute Differences,绝对差值和)是一种在图像处理和视频编码中常用的度量,用于计算两个图像块之间的差异。SAD值越小,表示两个图像块越相似。hadamard_ac计算:用于计算Hadam…...

什么是AR、VR、MR、XR?
时代背景 近年来随着计算机图形学、显示技术等的发展,视觉虚拟化技术得到了广泛的发展,并且越来越普及化,慢慢的也走入人们的视野。目前市场上视觉虚拟化技术的主流分为这几种 VR、AR、MR、XR。这几项技术并不是最近才出现的,VR的…...

Epic Games 商店面向欧盟 iPhone 用户上线
Epic Games Store 终于在欧盟推出,为玩家提供了不通过 App Store 就能在 iPhone上访问游戏的途径。在经历了漫长而昂贵的关于支付和竞争对手应用程序店面的法律战,以及公证方面的麻烦之后,Epic Games 成功地为App Store 带来了一个数字店面。…...
)
【计算机毕设项目】2025级计算机专业小程序项目推荐 (小程序+后台管理)
以下项目选题适合计算机专业大部分专业,技术栈主要为:前端小程序,后端Java语言,数据库MySQL 后台免费获取源码,可提供远程调试、环境安装配置服务。(文末有联系方式) 以下是本次部分项目推荐1…...

Fast API + LangServe快速搭建 LLM 后台
如果快速搭建一个 LLM 后台 API,使前端可以快速接入 LLM API。LangChain 或者 LlamaIndex 架构都可以快速集成各种大语言模型,本文将讲述如何通过 Fast API LangServe 快速的搭建一个后台 Rest API 服务。LLM 这些框架现在主打一个就是快速,…...

CSS继承、盒子模型、float浮动、定位、diaplay
一、CSS继承 1.文字相关的样式会被子元素继承。 2.布局样式相关的不会被子元素继承。(用inherit可以强行继承) 实现效果: 二、盒子模型 每个标签都有一个盒子模型,有内容区、内边距、边框、外边距。 从内到外:cont…...

使用百度文心智能体创建AI旅游助手
百度文心智能体平台为你开启。百度文心智能体平台,创建属于自己的智能体应用。百度文心智能体平台是百度旗下的智能AI平台,集成了先进的自然语言处理技术和人工智能技术,可以用来创建属于自己的智能体应用,访问官网链接࿱…...

斗破C++编程入门系列之四:运算符和表达式
鸡啄米C 记住首页不迷路: http://www.jizhuomi.com/software/129.html 斗破观看顺序: https://v.haohuitao.cc/yhplay/336-1-2.html 第一季☞第二季前2集☞特别篇1☞第二季3~12集☞特别篇2沙之澜歌☞第三季☞第四季☞三年之约☞缘起☞年番…...
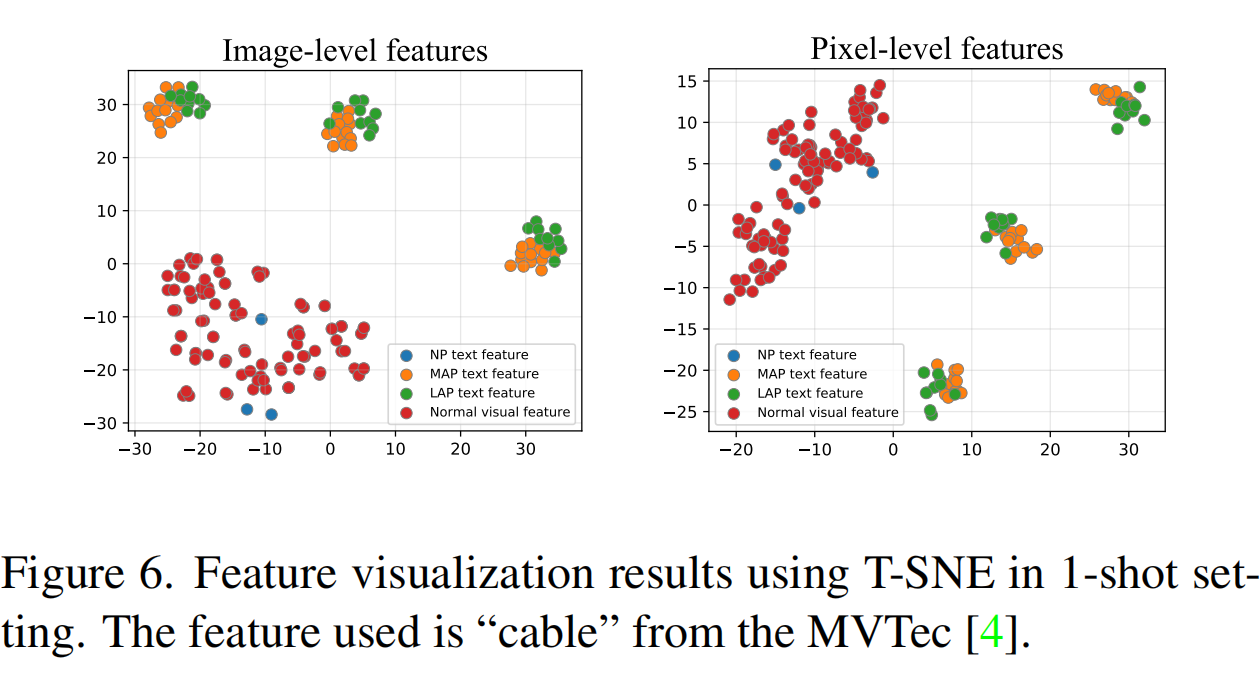
CVPR2024 | PromptAD: 仅使用正常样本进行小样本异常检测的学习提示
PromptAD: 仅使用正常样本进行小样本异常检测的学习提示 论文名称:PromptAD: Learning Prompts with only Normal Samples for Few-Shot Anomaly Detection 论文地址:https://arxiv.org/pdf/2404.05231 研究背景 异常检测(Anomaly Detecti…...

文件批量上传,oss使用时间戳解决同名问题 以及一些sql bug
1.文件批量上传 ApiOperation(value "文件批量上传")PostMapping("/multipleImageUpload")Transactional(rollbackFor Exception.class)public Result multipleImageUpload(ApiParam(name "files",value "文件",required true) R…...
机器学习——线性回归(sklearn)
目录 一、认识线性回归 1. 介绍 2. 多元线性回归的基本原理(LinearRegression) 二、多重共线性 1. 介绍 2. 多重共线性详细解释 三、岭回归(解决多重共线性问题) 1. 模型推导 2. 选取最佳的正则化参数取值 四、Lasso&am…...
 15)
Go 语言切片(Slice) 15
在 Go 语言中,切片(Slice)是一种可以容纳多个值的数据结构,它可以被视为一个可变的数组。切片是一个引用类型,它可以容纳任意类型的值,可以是整数、字符串、浮点数、结构体等。 切片的声明方式是使用 [] 语法,例如&am…...

嵌入式开发--STM32G030C8T6,写片上FLASH死机CFGBSY和写入出错
故障现象1 G0系列,写片上FLASH时,经常死机,而且按复位键都没用,属于不断电都救不回来的那种死法。这种情况一般是由硬件置位了某个标志导致,只有断电才能故障复原。 故障查找 检查FLASH的相关寄存器,发现…...
通过Fiddler抓包保存网页上的视频(包括Bilibili、B站和其他视频站)亲测可用
本文仅供学习交流用途 文中出现的信息仅为演示需要 请勿以任何方法剽窃、盗用任何视频作者的任何视频 有时候遇到一些素材想保存下来,但是网站不给保存,无论视频是否允许转载。这篇介绍一下最近发现的一个保存视频的方法。 不会介绍Fiddler了…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

react菜单,动态绑定点击事件,菜单分离出去单独的js文件,Ant框架
1、菜单文件treeTop.js // 顶部菜单 import { AppstoreOutlined, SettingOutlined } from ant-design/icons; // 定义菜单项数据 const treeTop [{label: Docker管理,key: 1,icon: <AppstoreOutlined />,url:"/docker/index"},{label: 权限管理,key: 2,icon:…...
