数据结构(6.2_1)——领接矩阵法
图的存储——邻接矩阵法
邻接矩阵(Adjacency Matrix)是一种使用二维数组来表示图的方法。在这种表示法中,矩阵的行和列都对应图的顶点。
特点
- 对于无向图,如果顶点i与顶点j之间有边,则矩阵的第i行第j列(记作
matrix[i][j])和第j行第i列的元素值为1(或者边的权重),否则为0。 - 对于有向图,如果存在一条从顶点i到顶点j的边,则
matrix[i][j]为1(或有向边的权重),否则为0。有向图的邻接矩阵一般不是对称的。 - 邻接矩阵适用于稠密图(边数接近顶点数平方的图)。
表示
- 设图G有
V个顶点,则邻接矩阵是一个V x V的矩阵。 - 对于无权图,
matrix[i][j]可以是0或1。 - 对于带权图,
matrix[i][j]可以是权重值,如果没有直接连接的边,则可以是无穷大或者一个特殊标记(比如null或者Infinity)。


优点
- 简单直观。
- 判断两个顶点之间是否存在边的时间复杂度为O(1)。
- 适用于快速查找两个顶点之间的边或计算顶点的度(对于无向图)。
缺点
- 如果图比较稀疏,则空间效率低下,因为很多位置都存储了0。
- 添加或删除顶点时,需要重新分配整个矩阵,成本较高。
如何求顶点的度、入度、出度
无向图:
第i个结点的度=第 i 行(或第i列)的非零元素个数
时间复杂度=O(n)

有向图:
第i个结点的出度=第 i 行的非零元素个数
第i个结点的入度=第 i 列的非零元素个数
第i个结点的度=第 i 行、第i列的非零元素个数之和

邻接矩阵法存储带权图(网)
带权图(网)是指图中每条边都有一个与之相关的权重。在邻接矩阵法中,带权图的存储可以通过将邻接矩阵中的元素设置为边的权重来表示。以下是带权图(网)使用邻接矩阵存储的详细说明。
特点
- 对于带权图,如果顶点i与顶点j之间有边,则邻接矩阵的第i行第j列(记作
matrix[i][j])的元素值为该边的权重。 - 如果顶点i与顶点j之间没有边,则
matrix[i][j]的元素值可以设置为无穷大(或者一个足够大的数,表示两个顶点之间没有直接连接)。 - 对于无向带权图,邻接矩阵是对称的,因为边
(i, j)和边(j, i)的权重是相同的。 - 对于有向带权图,邻接矩阵不一定对称,因为边
(i, j)的权重可以与边(j, i)的权重不同。
若出现0或∞则代表不存在边

- 方便地表示了边的权重。
- 快速查找两个顶点之间的边的权重,时间复杂度为O(1)。
- 便于计算最短路径等算法。
缺点
- 对于稀疏图,空间效率不高,因为大多数元素都是无穷大,表示没有边。
- 添加或删除顶点时,需要重新分配整个矩阵。
邻接矩阵的性能分析
空间复杂度:O(|V|^2)——只和顶点数相关,和实际的边数无关
适合存储稠密图
无向图的领接矩阵是对称矩阵,可以压缩存储(只存储上三角区/下三角区)

 领接矩阵法的性质
领接矩阵法的性质


总结:

相关文章:

数据结构(6.2_1)——领接矩阵法
图的存储——邻接矩阵法 邻接矩阵(Adjacency Matrix)是一种使用二维数组来表示图的方法。在这种表示法中,矩阵的行和列都对应图的顶点。 特点 对于无向图,如果顶点i与顶点j之间有边,则矩阵的第i行第j列(…...

诈骗未成功是否构成犯罪?
诈骗未成功不一定构成犯罪。在刑法上,构成诈骗罪需要满足特定的构成要件,包括有非法占有的目的、实施了虚构事实或隐瞒真相的行为、对方因此陷入错误认识并处分财产、行为人或第三方取得财产、被害人遭受财产损失。如果诈骗行为未能成功,即被…...
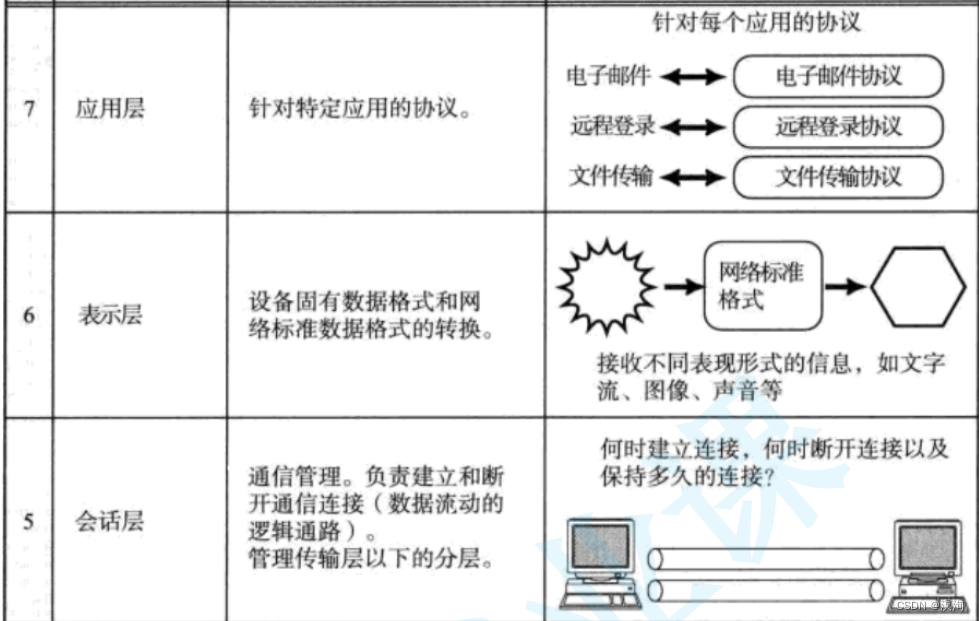
网络协议栈应用层的意义(内含思维导图和解析图通俗易懂超易理解)
绪论: “节省时间的方法就是全力以赴的将所要做的事情完美快速的做完,不留返工重新学习的时间,才能省下时间给其他你认为重要的东西。” 本章主要讲到OSI网络协议栈中的应用层的作用和再次在应用层的角度理解协议的具体意义,以及…...

【NXP-MCXA153】i2c驱动移植
介绍 I2C总线由飞利浦公司开发,是一种串行单工通信总线,它主要用于连接微控制器和其他外围设备并在总线上的器件之间传送信息(需要指定设备地址);常见的i2c设备有EEPROM、触摸屏、各种IoT传感器、时钟模块等&#x…...

C++(11)类语法分析(2)
C(10)之类语法分析(2) Author: Once Day Date: 2024年8月17日 一位热衷于Linux学习和开发的菜鸟,试图谱写一场冒险之旅,也许终点只是一场白日梦… 漫漫长路,有人对你微笑过嘛… 全系列文章可参考专栏: 源码分析_Once-Day的博客-CSDN博客 …...
)
数字验证每日十问--(3)
深拷贝和浅拷贝的区别? 当只拷贝对象中的成员变量和声明的句柄时,称为浅拷贝。浅拷贝只把对象中的句柄复制了,却没有复制句柄b所指向的对象。这会导致复制后,a2中的句柄b 和 a1 中的句柄b指向同一个对象,如果a2中的句…...

22.给定 n 对括号,实现一个算法生成所有可能的正确匹配的括号组合
22. Generate Parentheses 题目 给定 n 对括号,编写一个函数生成所有可能的正确匹配的括号组合。 例如,当 n = 3 时,可能的组合集合为: ["((()))","(()())","(())()","()(())","()()()" ]题目大意 给出 n 代表生成…...

检测到目标URL存在http host头攻击漏洞
漏洞描述 修复措施 方法一: nginx 的 default_server 指令可以定义默认的 server 去处理一些没有匹配到 server_name 的请求,如果没有显式定义,则会选取第一个定义的 server 作为 default_server。 server { …...

C++奇迹之旅:手写vector模拟实现与你探索vector 容器的核心机制与使用技巧
文章目录 📝基本框架🌠 构造和销毁🌉vector()🌉vector(const vector& v)🌉vector(size_t n, const T& value T())🌉赋值拷贝构造:vector<T>& operator(vector<T> v)&a…...

018、钩子函数 mounted和beforeDestroy、父组件向子组件传递参数 props 的使用
文章目录 1、mounted 和 beforeDestroy1.1、mounted1.2、beforeDestroy 2、父组件向子组件传递参数 props2.1、子组件定义2.2、父组件调用子组件并传参 3、完整例子3.1、父组件 Tags.vue3.2、子组件 TagsMenu.vue3.3、效果图 1、mounted 和 beforeDestroy 1.1、mounted mount…...

xlnt在Windows中的dll,lib生成
前言 花了半天时间想要把xlnt 集成到VS2022 Cmake项目中,以我目前掌握的能力,Cmake语法对于我来说难懂,对于只是使用过Cmake编译MySQL,或是其他lib,dll库的小白来说,不应该为了显示自己能力多么出众,强行去配置一些程序内容。 生活中没有绝对的事情,有舍有得. https://github…...

【网络】私有IP和公网IP的转换——NAT技术
目录 引言 NAT工作机制编辑 NAT技术的优缺点 优点 缺点 个人主页:东洛的克莱斯韦克-CSDN博客 引言 公网被子网掩码划分为层状结构,一个公网IP的机器又可以用很多私有IP搭建内网。在日常生活场景中用的都是私有IP,例如手机,…...

java 面试 PDF 资料整理
“尊贵的求知者,作者特此献上精心编纂的Java面试宝典PDF,这份资料凝聚了无数面试精华与实战经验,是通往Java技术殿堂的钥匙。若您渴望在Java编程的求职之路上稳健前行,只需轻轻一点,完成这象征支持与认可的一键三联&am…...

初步认识Linux系统
前言 Linux系统具有许多优点,不仅系统性能稳定,而且是开源软件。其核心防火墙组件性能高效、配置简单,保证了系统的安全。在很多企业网络中,为了追求速度和安全,Linux不仅仅是被网络运维人员当作服务器使用,…...

JavaScript AI 编程助手
JavaScript AI 编程助手 引言 随着人工智能技术的飞速发展,编程领域也迎来了前所未有的变革。JavaScript,作为全球最流行的编程语言之一,其与AI的结合为开发者带来了巨大的便利和无限的可能性。本文将探讨JavaScript AI编程助手的定义、功能…...

达梦数据库的系统视图v$datafile
达梦数据库的系统视图v$datafile 达梦数据库的V$DATAFILE 是一个重要的系统视图,提供了有关数据库数据文件的信息。 V$DATAFILE 系统视图 V$DATAFILE 视图用于显示数据库中每一个数据文件的详细信息。通过查询这个视图,数据库管理员可以了解数据文件的…...

Triton/window安装: triton-2.0.0-cp310-cp310-win_amd64.whl文件
下面这个github仓: https://github.com/PrashantSaikia/Triton-for-Windows/tree/main 安装命令也很简单,下载到本地后运行: pip install triton-2.0.0-cp310-cp310-win_amd64.whl...
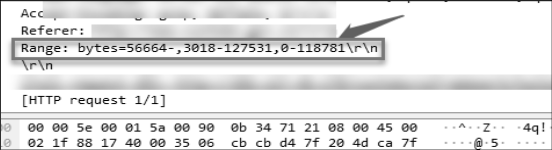
应急响应-DDOS-典型案例
某单位遭受DDoS攻击事件如下 事件背景 2019年2月17日,某机构门户网站无法访问,网络运维人员称疑似遭受DDoS攻击,请求应急响应工程师协助。 事件处置 应急响应工程师在达到现场后,通过查看流量设备,发现攻击者使用僵…...

JAVA学习之知识补充(下)
六:File类与IO流: 这里给出三种常见的初始化方法: 通过文件路径初始化: File file new File("C:/example/test.txt");这种方法用于创建一个文件对象,该文件对象表示指定路径的文件或目录。例如:File fil…...

qt生成一幅纯马赛克图像
由于项目需要,需生成一幅纯马赛克的图像作为背景,经过多次测试成功,记录下来。 方法一:未优化方法 1、代码: #include <QImage> #include <QDebug> #include <QElapsedTimer>QImage generateMosa…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
