【数据结构】并查集
目录
一:用途
二:实现 O(1)
三:例题
例题1:集合
例题2:连通图无向
例题3:acwing 240 食物链
一:用途
- 将两个集合合并
- 询问两个元素是否在一个集合当中
二:实现 O(1)
每个集合用一棵树表示,树根的编号就是整个集合的编号。每个节点存储它的父节点,p[x]表示x的父节点。
- 问题一:如何判断树根:if(p[x]==x)
- 问题二:如何求x的集合编码:while(p[x]!=x) x=p[x];
- 问题三:如何合并两个集合:px是x的集合编码,py是y的集合编码。p[x]=y //直接将树y插到树x上作为子树。
(1)朴素并查集:int p[N]; //存储每个点的祖宗节点// 返回x的祖宗节点int find(int x){if (p[x] != x) p[x] = find(p[x]);return p[x];}// 初始化,假定节点编号是1~nfor (int i = 1; i <= n; i ++ ) p[i] = i;// 合并a和b所在的两个集合:p[find(a)] = find(b);(2)维护size的并查集: //需要求集合点的数量int p[N], size[N];//p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义,表示祖宗节点所在集合中的点的数量// 返回x的祖宗节点int find(int x)// 初始化,假定节点编号是1~nfor (int i = 1; i <= n; i ++ ){p[i] = i; size[i] = 1;}// 合并a和b所在的两个集合:size[find(b)] += size[find(a)];p[find(a)] = find(b);(3)维护到祖宗节点距离的并查集:int p[N], d[N];//p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离// 返回x的祖宗节点int find(int x){if (p[x] != x){int u = find(p[x]);d[x] += d[p[x]];p[x] = u;}return p[x];}// 初始化,假定节点编号是1~nfor (int i = 1; i <= n; i ++ ){p[i] = i;d[i] = 0;}// 合并a和b所在的两个集合:p[find(a)] = find(b);d[find(a)] = distance; // 根据具体问题,初始化find(a)的偏移量
三:例题
例题1:集合
一共有 n 个数,编号是 1∼n,最开始每个数各自在一个集合中。
现在要进行 m 个操作,操作共有两种:
M a b,将编号为 a 和 b 的两个数所在的集合合并,如果两个数已经在同一个集合中,则忽略这个操作;
Q a b,询问编号为 a 和 b 的两个数是否在同一个集合中;
输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为 M a b 或 Q a b 中的一种。
输出格式
对于每个询问指令 Q a b,都要输出一个结果,如果 a 和 b 在同一集合内,则输出 Yes,否则输出 No。
每个结果占一行。
数据范围
1≤n,m≤1e5
输入样例:
4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4输出样例:
Yes
No
Yes
#include<iostream>using namespace std;const int N = 100010;int n, m;
int p[N]; //存储父节点int find(int x) // 返回x的祖宗节点
{if(p[x] != x) p[x] = find(p[x]);return p[x];
}int main()
{cin >> n >> m;for(int i = 1; i <= n; i++) p[i] = i; //初始化while(m--){char op[2];int a, b;cin >> op >> a >> b;if(*op == 'M') p[find(a)] = find(b); //合并a和belse {if(find(a) == find(b)) cout << "Yes" << endl;else cout << "No" << endl;}}return 0;
}例题2:连通图无向
给定一个包含 n 个点(编号为 1∼n1∼n)的无向图,初始时图中没有边。
现在要进行 m 个操作,操作共有三种:
C a b,在点 a 和点 b 之间连一条边,aa 和 b 可能相等;
Q1 a b,询问点 a 和点 b 是否在同一个连通块中,a 和 b可能相等;
Q2 a,询问点 a所在连通块中点的数量;
输入格式
第一行输入整数 n 和 m。
接下来 m行,每行包含一个操作指令,指令为 C a b,Q1 a b 或 Q2 a 中的一种。
输出格式
对于每个询问指令 Q1 a b,如果 aa 和 bb 在同一个连通块中,则输出 Yes,否则输出 No。
对于每个询问指令 Q2 a,输出一个整数表示点 a 所在连通块中点的数量
每个结果占一行。
数据范围
1≤n,m≤1051≤n,m≤105
输入样例:
5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5
输出样例:
Yes
2
3#include<iostream>
using namespace std;
const int N=1e5+10;
int n,m,p[N],sizee[N];
//p[]存储每个点 sizee[]存储根节点所拥有的子节点数
//并查集中的find函数
int find(int x)
{if(p[x]!=x) p[x]=find(p[x]);return p[x];
}int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) {p[i]=i;sizee[i]=1;//每个节点作为根节点 集合中只有自己一个元素}while(m--){char op[3];int a,b;scanf("%s",op);if(op[0]=='C')//连边,就是合并{scanf("%d%d",&a,&b);if(find(a)==find(b)) continue;//在一个集合里 就跳出sizee[find(b)]+=sizee[find(a)];//将节点数加到新根节点数上//例如原来a连通块里有3个节点 b里面有4个节点//a连到b的连通块里 那么b里面现在有7个节点p[find(a)]=find(b);//根节点等于b的根节点}else if(op[1]=='1'){scanf("%d%d",&a,&b);if(find(a)==find(b)) puts("Yes");//在同一个集合else puts("No");}else{scanf("%d",&a);printf("%d\n",sizee[find(a)]);//输出根节点的数}}return 0;
} 例题3:acwing 240 食物链
相关文章:

【数据结构】并查集
目录 一:用途 二:实现 O(1) 三:例题 例题1:集合 例题2:连通图无向 例题3:acwing 240 食物链 一:用途 将两个集合合并询问两个元素是否在一个集合当中 二:实现 O(1) 每…...

软考--网络攻击分类
网络攻击的主要手段包括口令入侵、放置特洛伊木马程序、拒绝服务(DoS)攻击、端口扫描、网络监听、欺骗攻击和电子邮件攻击等。口令入侵是指使用某些合法用户的账号和口令登录到目的主机,然后再实施攻击活动。特洛伊木马(Trojans)程序常被伪装…...

蓝桥杯刷题冲刺 | 倒计时17天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.长草2.分考场1.长草 题目 链接: 长草 - 蓝桥云课 (lanqiao.cn) 题目描述 小明有一…...

冲击蓝桥杯-并查集,前缀和,字符串
目录 前言 一、并查集 1、并查集的合并(带路径压缩) 2、询问是否为同一个集合 3、例题 二、前缀和 1 、前缀和是什么 2、经典题目 三- 字符串处理 1、字符串的插入 2、字符串转化为int类型 3、字符反转 前言 并查集合前缀,字符串…...

【matlab学习笔记】线性方程组求解方法
线性方程组求解方法2.1 求逆法实现方式例子2.2 分解法LU分解(Doolittle分解)实现方法例子QR分解法实现方法例子Cholesky 分解法实现方法例子奇异值分解法实现方法例子Hessenberg 分解实现方法例子Schur 分解实现方法例子2.3 迭代法逐次迭代法里查森迭代法…...

Python带你一键下载到最新章节,不付费也能看
前言 大家早好、午好、晚好吖 ❤ ~欢迎光临本文章 完整源码、素材皆可点击文章下方名片获取此处跳转 开发环境: python 3.8 运行代码 pycharm 2022.3 辅助敲代码 requests 发送请求/第三方模块 模块安装:win R 输入cmd 输入安装命令 pip install 模块名 如果…...
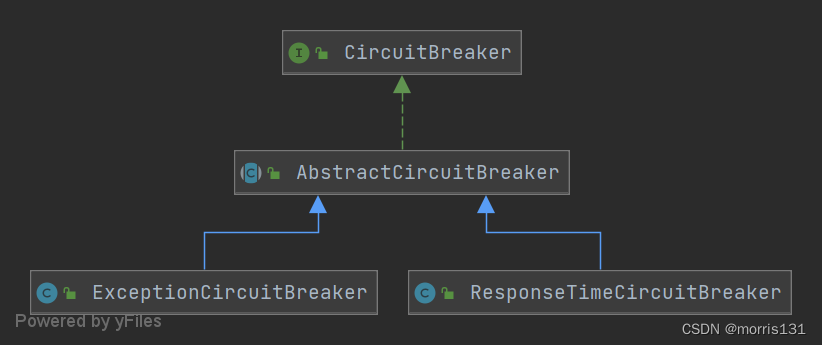
【sentinel】熔断降级规则详解及源码分析
概述 除了流量控制以外,对调用链路中不稳定的资源进行熔断降级也是保障高可用的重要措施之一。一个服务常常会调用别的模块,可能是另外的一个远程服务、数据库,或者第三方API等。例如,支付的时候,可能需要远程调用银联…...

ffplay源码分析-main函数入口分析
ffplay源码分析-main函数入口分析 基于ffmpeg6.0源码分析。 流程 使用ffplay播放视频文件,会触发main函数的调用。main函数中会进行以下操作: 从命令行中解析日志级别、日志是否需要落文件、是否要输出banner信息。banner信息包含版权、库的版本。注…...

C++三种继承方式
C继承的一般语法为:class 派生类名:[继承方式] 基类名{派生类新增加的成员};继承方式限定了基类成员在派生类中的访问权限,包括 public(公有的)、private(私有的)和 protected&#…...

【Android -- 软技能】《软技能:代码之外的生存指南》之好书推荐(一)
前言 这是一本由美国的一个软件开发人员写的,但书中除了有 Java 、C# 几个单词外,没有一行代码。 因为这本书讲的是代码之外的东西。 文章目录结构: 1. 职业 从业心态:说白了就是要有责任心,把每份工作要当成是自…...

Nginx可视化管理工具 - Nginx Proxy Manager
一、介绍 nginx-proxy-manager 是一个反向代理管理系统,它基于Nginx,具有漂亮干净的 Web UI。还可以获得受信任的 SSL 证书,并通过单独的配置、自定义和入侵保护来管理多个代理。 其官网地址如下: https://nginxproxymanager.com/ 二、安装 第一步:192.168.1.108服务…...

https是如何保证安全的
在学习http与https的区别的时候,我们通常从以下几点出发:http是超文本传输协议,是明文传输,有安全风险,https在TCP和http网络层之间加入了SSL/TLS安全协议,使得报文能够加密传输http连接简单,三…...

ubuntu下使用GCC开发单片机的过程
以下是一个简单的单片机C程序示例,实现的功能是控制LED灯的闪烁: #include <reg52.h> // 导入单片机的寄存器定义void main() {while(1) { // 无限循环P1 = 0x00; // P1口输出低电平delay(1000); // 延时1秒P1 = 0xff; // P1口输出高电平delay(1000); // 延时1秒…...
人工智能能否取代软硬件开发工程师
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl 人工智能发展趋势 随着AI技术的不断发展,它正在改变我们的生活方式、商业模式和工作方式。人工智能技术的发展一直处于快速变化和持续创新的状态,以下…...

BPI-R3开发板 - uboot编译
一. 获取源码 https://github.com/mtk-openwrt/u-boot 二. 编译步骤 编译环境为ubuntu 18.04。交叉编译工具链我用的是openwrt编译生成的工具链,并设置到环境变量,如下: export PATH$PATH:/root/mt8976/BPI-R3-OPENWRT-V21.02.3-main/staging…...

优秀程序员的5个特征,你在第几层?
每个人程序员都对未来的职业发展有着憧憬和规划,要做架构师、要做技术总监、要做CTO。但现实总是复杂的,日复一日的工作与生活总能让人一次又一次地陷入迷茫。大部分原因就是对职业发展轨迹和自我能力提升的一般规律缺乏认识,做事找不到方向或…...
JAVA Session会话 Thymeleaf - 视图模板技术配置步骤
JAVAWebSession会话会话跟踪技术session保存作用域Thymeleaf - 视图模板技术配置过程Session会话 HTTP是无状态的:服务器无法区分这两个请求是同一个客户端发过来的,还是不同的客户端发过来的 现实问题:第一次请求是添加商品到购物车&#x…...

Linux编译cpprestsdk库
本文用的Linux系统为Ubuntu22.04,自带GCC11.3.0。 依赖 ①编译需要boost库,本文用的库版本为boost-1.82.0.beta1.tar.gz。 ②编译需要openssl库,这里使用的版本为openssl-1.1.1s.tar.gz。 ③编译需要cmake库,本文使用的是cmake-3…...
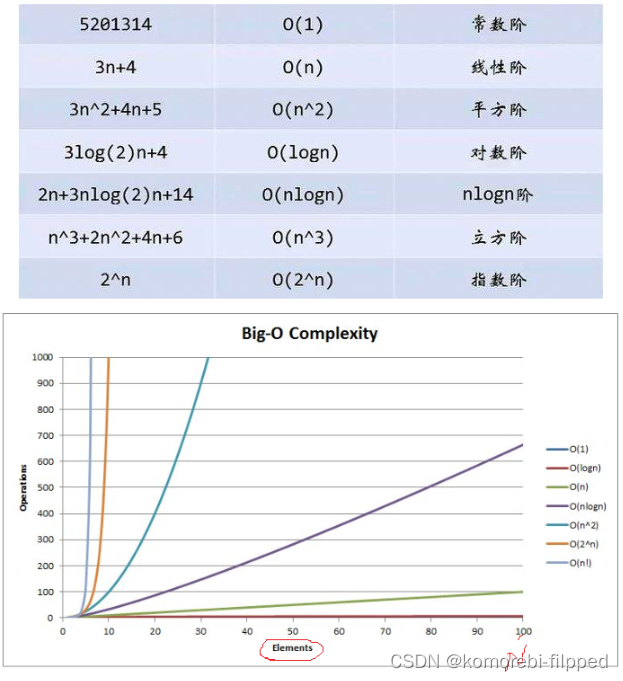
算法的时间复杂度和空间复杂度
目录 1 如何衡量一个算法的好坏 2.时间复杂度 2.1 时间复杂度的概念 2.2 大O的渐进表示法 2.3常见代码举例 2.3.1 Func2 O(N) 2.3.2 Func3 O(MN) 2.3.3 Func4 O(1) 2.3.4 Func5 strchr O(N) 2.3.5 Func6 冒泡排序 O(N^2) 2.3.6 Func7 二分…...
基本认识vue3
一、基本搭建 项目搭建 使用 最新的 Vue3 TS Vite项目 执行命令 (本项目采用如下方式) npm create vitelatest my-vite-app --template vue-ts或者 运行项目 npm install npm run dev项目搭建初始化目录 新搭建的项目可能会遇到个问题…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...

Git 命令全流程总结
以下是从初始化到版本控制、查看记录、撤回操作的 Git 命令全流程总结,按操作场景分类整理: 一、初始化与基础操作 操作命令初始化仓库git init添加所有文件到暂存区git add .提交到本地仓库git commit -m "提交描述"首次提交需配置身份git c…...

基于Java项目的Karate API测试
Karate 实现了可以只编写Feature 文件进行测试,但是对于熟悉Java语言的开发或是测试人员,可以通过编程方式集成 Karate 丰富的自动化和数据断言功能。 本篇快速介绍在Java Maven项目中编写和运行测试的示例。 创建Maven项目 最简单的创建项目的方式就是创建一个目录,里面…...

Neo4j 完全指南:从入门到精通
第1章:Neo4j简介与图数据库基础 1.1 图数据库概述 传统关系型数据库与图数据库的对比图数据库的核心优势图数据库的应用场景 1.2 Neo4j的发展历史 Neo4j的起源与演进Neo4j的版本迭代Neo4j在图数据库领域的地位 1.3 图数据库的基本概念 节点(Node)与关系(Relat…...
