基于堆与AdjustDown的TOP-K问题
TIPS


TOP-K问题
TOP-K问题:就是说现在比如说有n个数据,然后需要从这n个数据里面找到最大的或最小的前k个。
一般来讲思路的话就是:先把这n个数据给他建一个堆,建堆完成之后,然后就去调堆,然后大概只需要调k次,然后就可以把前k个数据给他找到。
但比如说这个N它有时候会很大很大,比如说100亿,那这样的话100亿整数大概需要占40gb的内存。如果说还是按上面这个方法去做的话,光去建一个堆就要去申请40gb的内存,不可能啊。1G大约10亿字节
比如说现在n是100亿,也就是说有100亿个整数,然后比如说需要找到前50大的整数,该怎么办?
对于这种topk问题的话,实际上有个贼简单的方法。他现在题目中不是说有100亿个整数,然后需要去找到前50大的整数。我就直接利用他100亿个数据当中前50个数据先去建一个堆,而且是小根堆。然后去遍历剩下的所有数据,如果说那个数据比我这个堆顶的数据要大,就代替它进堆并向下调整Adjustadown。
这个方法他真正厉害的地方就在于他是一个小根堆。因为如果这样子的话,最大的前k个数一定能够进堆,就是说不存在,比如说有一个特别特别大的树放在堆顶,然后阻挡最大的前k个数进入。因为首先我这个堆里面的数据总共也就是k一个,其次就是这是一个小根堆,比较大的树它都是在堆底,就意味着在堆顶上面的数据是最小的。
如果说我要从非常非常非常多的数据当中找到前k个最小的数据,那我这时候就要建一个大根堆(有k个节点)。如果说我要求非常非常非常多的数据当中找到前k个最大的数据,那我这时候就要建一个小根堆(有k个节点)。
然后接下来依次去遍历所有的那些非常多的数据,然后与堆顶的元素进行比较,比如说我要求前k个最小的,我现在已经建了一个大根堆,如果说我遍历的元素比堆顶的元素要来的小,那就先去取代堆顶,然后接下来AdjustDown;如说我要求前k个最大的,我现在已经建了一个小根堆,如果说我遍历的元素比堆顶的元素要来的大,那就先去取代堆顶,然后接下来AdjustDown。这个与之前的堆排序有点差不多,都是有点逆直觉:比如说在堆排序当中,如果我要升序排列,就要建大根堆;如果说我要降序排列,就要减小根堆
然后popk问题不要与堆排序问题扯到一起,因为这个的话只涉及到建堆AdjustDown,并没有涉及到调堆。但如果说有额外要求的话,说在很多很多数据当中,求出前k个最小的数据,并且对于这k个数据也要进行排序的话,那么这时候就要额外加上堆排序的调堆

TOP-K问题的演示解决
这个先必须得有
void Swap(int* p1, int* p2)
{assert(p1 && p2);int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void AdjustDown(int* a, int parent, int n)
{assert(a);int child = 2 * parent + 1;while (child < n){if (child+1<n && a[child] < a[child + 1]){child++;}if (a[parent] < a[child]){Swap(a + parent, a + child);parent = child;child = 2 * parent + 1;}else{break;}}
}造数据
#define ALL_NUMBER 10000000
#define SELECT_NUMBER 10
void CreateNumber()
{srand((unsigned int)time(NULL));FILE* pf = fopen("test.txt", "w");assert(pf);for (int i = 0; i < ALL_NUMBER; i++){fprintf(pf, "%d", rand() * 12345 % 1000000);}fclose(pf);pf = NULL;
}TOP-K过程
void PrintPopK()
{FILE* pf = fopen("text.txt", "r");assert(pf);//建堆int arr[SELECT_NUMBER] = { 0 };for (int i = 0; i < SELECT_NUMBER; i++){fscanf(pf, "%d", &arr[i]);}for (int i = (SELECT_NUMBER - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, i, SELECT_NUMBER);}//遍历所有数据,看能否入堆int val;int ret;while ((ret = fscanf(pf, "%d", &val)) != EOF){if (val > arr[0]){arr[0] = val;AdjustDown(arr, 0, SELECT_NUMBER);}}//此刻,前k小的数已经在堆里面了,我还想排序一下int end = SELECT_NUMBER - 1;while (end > 0){Swap(arr + 0, arr + end);AdjustDown(arr, 0, end);end--;}//最终打印结果for (int i = 0; i < SELECT_NUMBER; i++){printf("%d ", arr[i]);}fclose(pf);pf = NULL;
}总代码
#define ALL_NUMBER 1000000
#define SELECT_NUMBER 10
void CreateNumber()
{FILE* pf = fopen("text.txt", "w");assert(pf);for (int i = 0; i < ALL_NUMBER; i++){fprintf(pf, "%d\n", rand() * (rand()%10000) % 1000000);}fclose(pf);pf = NULL;
}void PrintPopK()
{FILE* pf = fopen("text.txt", "r");assert(pf);//建堆int arr[SELECT_NUMBER] = { 0 };for (int i = 0; i < SELECT_NUMBER; i++){fscanf(pf, "%d", &arr[i]);}for (int i = (SELECT_NUMBER - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, i, SELECT_NUMBER);}//遍历所有数据,看能否入堆int val;int ret;while ((ret = fscanf(pf, "%d", &val)) != EOF){if (val > arr[0]){arr[0] = val;AdjustDown(arr, 0, SELECT_NUMBER);}}//此刻,前k小的数已经在堆里面了,我还想排序一下int end = SELECT_NUMBER - 1;while (end > 0){Swap(arr + 0, arr + end);AdjustDown(arr, 0, end);end--;}//最终打印结果for (int i = 0; i < SELECT_NUMBER; i++){printf("%d ", arr[i]);}fclose(pf);pf = NULL;
}int main()
{srand((unsigned int)time(NULL));CreateNumber();PrintPopK();return 0;
}
体悟:
TOP-K问题他主要就是利用在堆当中所有的元素中堆顶是最值,因此每次就要去堆顶比较,并不断试图去代替他,一旦把他代替了之后,堆被破坏了,这时候还要复原回堆,然后再去利用堆着那个特别厉害的性质(堆顶元素是所有元素当中的最值)
相关文章:

基于堆与AdjustDown的TOP-K问题
TIPSTOP-K问题TOP-K问题:就是说现在比如说有n个数据,然后需要从这n个数据里面找到最大的或最小的前k个。一般来讲思路的话就是:先把这n个数据给他建一个堆,建堆完成之后,然后就去调堆,然后大概只需要调k次&…...
在CentOS上安装Docker引擎
1,先决条件#### 1-1操作系统要求1-2 卸载旧版本 2,安装方法2-1使用存储库安装设置存储库安装 Docker 引擎 本文永久更新地址: 官方地址:https://docs.docker.com/engine/install/centos/ 1,先决条件 #### 1-1操作系统要求 要安装 Docker Engine,您需要…...

【10】核心易中期刊推荐——模式识别与机器学习
🚀🚀🚀NEW!!!核心易中期刊推荐栏目来啦 ~ 📚🍀 核心期刊在国内的应用范围非常广,核心期刊发表论文是国内很多作者晋升的硬性要求,并且在国内属于顶尖论文发表,具有很高的学术价值。在中文核心目录体系中,权威代表有CSSCI、CSCD和北大核心。其中,中文期刊的数…...

【数据结构】并查集
目录 一:用途 二:实现 O(1) 三:例题 例题1:集合 例题2:连通图无向 例题3:acwing 240 食物链 一:用途 将两个集合合并询问两个元素是否在一个集合当中 二:实现 O(1) 每…...

软考--网络攻击分类
网络攻击的主要手段包括口令入侵、放置特洛伊木马程序、拒绝服务(DoS)攻击、端口扫描、网络监听、欺骗攻击和电子邮件攻击等。口令入侵是指使用某些合法用户的账号和口令登录到目的主机,然后再实施攻击活动。特洛伊木马(Trojans)程序常被伪装…...

蓝桥杯刷题冲刺 | 倒计时17天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.长草2.分考场1.长草 题目 链接: 长草 - 蓝桥云课 (lanqiao.cn) 题目描述 小明有一…...

冲击蓝桥杯-并查集,前缀和,字符串
目录 前言 一、并查集 1、并查集的合并(带路径压缩) 2、询问是否为同一个集合 3、例题 二、前缀和 1 、前缀和是什么 2、经典题目 三- 字符串处理 1、字符串的插入 2、字符串转化为int类型 3、字符反转 前言 并查集合前缀,字符串…...

【matlab学习笔记】线性方程组求解方法
线性方程组求解方法2.1 求逆法实现方式例子2.2 分解法LU分解(Doolittle分解)实现方法例子QR分解法实现方法例子Cholesky 分解法实现方法例子奇异值分解法实现方法例子Hessenberg 分解实现方法例子Schur 分解实现方法例子2.3 迭代法逐次迭代法里查森迭代法…...

Python带你一键下载到最新章节,不付费也能看
前言 大家早好、午好、晚好吖 ❤ ~欢迎光临本文章 完整源码、素材皆可点击文章下方名片获取此处跳转 开发环境: python 3.8 运行代码 pycharm 2022.3 辅助敲代码 requests 发送请求/第三方模块 模块安装:win R 输入cmd 输入安装命令 pip install 模块名 如果…...
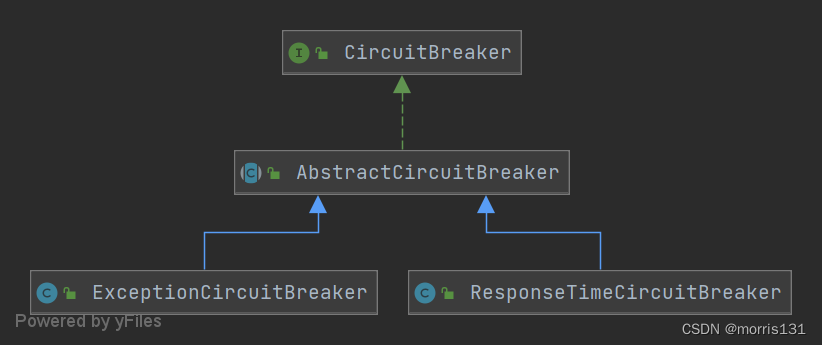
【sentinel】熔断降级规则详解及源码分析
概述 除了流量控制以外,对调用链路中不稳定的资源进行熔断降级也是保障高可用的重要措施之一。一个服务常常会调用别的模块,可能是另外的一个远程服务、数据库,或者第三方API等。例如,支付的时候,可能需要远程调用银联…...

ffplay源码分析-main函数入口分析
ffplay源码分析-main函数入口分析 基于ffmpeg6.0源码分析。 流程 使用ffplay播放视频文件,会触发main函数的调用。main函数中会进行以下操作: 从命令行中解析日志级别、日志是否需要落文件、是否要输出banner信息。banner信息包含版权、库的版本。注…...

C++三种继承方式
C继承的一般语法为:class 派生类名:[继承方式] 基类名{派生类新增加的成员};继承方式限定了基类成员在派生类中的访问权限,包括 public(公有的)、private(私有的)和 protected&#…...

【Android -- 软技能】《软技能:代码之外的生存指南》之好书推荐(一)
前言 这是一本由美国的一个软件开发人员写的,但书中除了有 Java 、C# 几个单词外,没有一行代码。 因为这本书讲的是代码之外的东西。 文章目录结构: 1. 职业 从业心态:说白了就是要有责任心,把每份工作要当成是自…...

Nginx可视化管理工具 - Nginx Proxy Manager
一、介绍 nginx-proxy-manager 是一个反向代理管理系统,它基于Nginx,具有漂亮干净的 Web UI。还可以获得受信任的 SSL 证书,并通过单独的配置、自定义和入侵保护来管理多个代理。 其官网地址如下: https://nginxproxymanager.com/ 二、安装 第一步:192.168.1.108服务…...

https是如何保证安全的
在学习http与https的区别的时候,我们通常从以下几点出发:http是超文本传输协议,是明文传输,有安全风险,https在TCP和http网络层之间加入了SSL/TLS安全协议,使得报文能够加密传输http连接简单,三…...

ubuntu下使用GCC开发单片机的过程
以下是一个简单的单片机C程序示例,实现的功能是控制LED灯的闪烁: #include <reg52.h> // 导入单片机的寄存器定义void main() {while(1) { // 无限循环P1 = 0x00; // P1口输出低电平delay(1000); // 延时1秒P1 = 0xff; // P1口输出高电平delay(1000); // 延时1秒…...
人工智能能否取代软硬件开发工程师
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl 人工智能发展趋势 随着AI技术的不断发展,它正在改变我们的生活方式、商业模式和工作方式。人工智能技术的发展一直处于快速变化和持续创新的状态,以下…...

BPI-R3开发板 - uboot编译
一. 获取源码 https://github.com/mtk-openwrt/u-boot 二. 编译步骤 编译环境为ubuntu 18.04。交叉编译工具链我用的是openwrt编译生成的工具链,并设置到环境变量,如下: export PATH$PATH:/root/mt8976/BPI-R3-OPENWRT-V21.02.3-main/staging…...

优秀程序员的5个特征,你在第几层?
每个人程序员都对未来的职业发展有着憧憬和规划,要做架构师、要做技术总监、要做CTO。但现实总是复杂的,日复一日的工作与生活总能让人一次又一次地陷入迷茫。大部分原因就是对职业发展轨迹和自我能力提升的一般规律缺乏认识,做事找不到方向或…...
JAVA Session会话 Thymeleaf - 视图模板技术配置步骤
JAVAWebSession会话会话跟踪技术session保存作用域Thymeleaf - 视图模板技术配置过程Session会话 HTTP是无状态的:服务器无法区分这两个请求是同一个客户端发过来的,还是不同的客户端发过来的 现实问题:第一次请求是添加商品到购物车&#x…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...
