当前位置：首页 > news >正文

机器学习第十一章--特征选择与稀疏学习

news 2026/2/10 6:12:21

一、子集搜索与评价

我们将属性称为 “特征”(feature），对当前学习任务有用的属性称为 “相关特征”(relevant feature）、没什么用的属性称为 “无关特征”(irrelevant feature)．从给定的特征集合中选择出相关特征子集的过程，称为“特征选择”(feature selection).

有两个很重要的原因：减轻维数灾难问题、降低学习任务的难度.

“冗余特征”(redundant feature):所包含的信息能从其他特征中推演出来.冗余特征在很多时候不起作用，去除它们会减轻学习过程的负担.但有时冗余特征会降低学习任务的难度.

“子集搜索”(subset search)：：

“前向”(forward)搜索：初始将每个特征当做一个候选特征子集，然后从当前所有的候选子集中选择出最佳的特征子集；接着在上一轮选出的特征子集中添加一个新的特征，同样地选出最佳特征子集；最后直至选不出比上一轮更好的特征子集。
“后向”(backward)搜索：初始将所有特征作为一个候选特征子集；接着尝试去掉上一轮特征子集中的一个特征并选出当前最优的特征子集；最后直到选不出比上一轮更好的特征子集。
“双向”(bidirectional)搜索：将前向搜索与后向搜索结合起来，即在每一轮中既有添加操作也有剔除操作。

“子集评价”(subset evaluation)：

给定数据集D，假定D中第i类样本所占的比例为 $p_{i}(i=1,2,...,\left | y \right |)$ ．假定样本属性均为离散型.对属性子集A,假定根据其取值将D分成了V个子集 $\left \{ D^{1},D^{2},...,D^{V} \right \}$ ,每个子集中的样本在A上取值相同,属性子集A的信息增益:

将特征子集搜索机制与子集评价机制相结合,即可得到特征选择方法.
常见的特征选择方法大致可分为三类:过滤式(filter)、包裹式(wrapper)和嵌入式(embedding).

二、过滤式选择

过滤式方法先对数据集进行特征选择,然后再训练学习器.
Relief (Relevant Features)设计了一个“相关统计量”来度量特征的重要性.该统计量是一个向量,其每个分量分别对应于一个初始特征,最终只需指定一个阈值r,然后选择比T大的相关统计量分量所对应的特征即可;也可指定欲选取的特征个数k,然后选择相关统计量分量最大的k个特征.
Relief的关键是如何确定相关统计量．给定训练集{ $\left \{ (x_{1},y_{1}),(x_{2},y_{2}),...,(x_{m},y_{m}) \right \}$ }，对每个示例 $x_{i}$ ,，Relief 先在 $x_{i}$ 的同类样本中寻找其最近邻 $x_{i,nh}$ ，称为“猜中近邻”(near-hit)，再从 $x_{i}$ 的异类样本中寻找其最近邻 $x_{i,nm}$ ,称为“猜错近邻”(near-miss)，然后,相关统计量对应于属性j的分量为

Relief是为二分类问题设计的,其扩展变体Relief-F能处理多分类问题.其相关统计量对应于属性j的分量为：

三、包裹式选择

包裹式特征选择直接把最终将要使用的学习器的性能作为特征子集的评价准则.
包裹式特征选择比过滤式特征选择更好,计算开销通常更大.

LVW (Las Vegas Wrapper)在拉斯维加斯方法(Las Vegas metnod)框架下使用随机策略来进行子集搜索，并以最终分类器的误差为特征子集评价准则.

算法描述:

若有运行时间限制,则有可能给不出解.

四、嵌入式选择与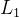 $L_{1}$ 正则化

嵌入式特征选择是将特征选择过程与学习器训练过程融为一体,两者在同一个优化过程中完成,即在学习器训练过程中自动地进行了特征选择.

给定数据集我们考虑最简单的线性回归模型,以平方误差为损失函数,则优化目标为

当样本特征很多,而样本数相对较少时，上式很容易陷入过拟合.为了缓解过拟合问题,可对上式引入正则化项.

若使用 $L_{2}$ 范数正则化,则有“岭回归”(ridge regression)

采用 $L_{1}$ 范数，则有LASSO (Least Absolute Shrinkage andSelection Operator)

$L_{1}$ 范数和 $L_{2}$ 范数正则化都有助于降低过拟合风险, $L_{1}$ 比 $L_{2}$ 更易于获得“稀疏”(sparse)解，即它求得的w会有更少的非零分量.

L正则化问题的求解可使用近端梯度下降(Proximal Gradient Descent,简称PGD) .具体来说，令 $\nabla$ 表示微分算子,对优化目标

若f(x可导，且 $\nabla$ f满足L-Lipschitz条件,即存在常数L>0使得

则在 $x_{k}$ 附近可将f(x)通过二阶泰勒展式近似为

最小值在如下 $x_{k+1}$ 获得:

推广到正则化，加一个正则项求最小值：

得到每个分量的解：

五、稀疏表示与字典学习

为普通稠密表达的样本找到合适的字典，将样本转化为合适的稀疏表示形式，从而使学习任务得以简化,模型复杂度得以降低,通常称为“字典学习”(dictionary learning)（侧重于学得字典的过程）,亦称“稀疏编码”(sparse coding)（侧重于对样本进行稀疏表达的过程）.下面不做区分。

给定数据集 $\left \{ x_{1} ,x_{2} ,...x_{m} \right \}$ ，字典学习最简单的形式为

受LASSO的启发,我们可采用变量交替优化的策略来求解式.

首先在第一步,我们固定住字典B,为每个样本 $x_{i}$ 找到相应的 $\alpha _{i}$ :

在第二步,我们固定住 $\alpha _{i}$ 来更新字典B:

基于逐列更新策略的KSVD:令 $b_{i}$ 表示字典矩阵B的第i列, $\alpha ^{i}$ 表示稀疏矩阵A的第i行，上式可重写为

六、压缩感知

现实，常对数据进行压缩，方便处理，但在传递的时候，因为各种情况会出现信息损失，通过压缩感知来解决这个问题

假定我们以远小于奈奎斯特采样定理要求的采样率进行采样，即

$y=\Phi x$

这个信号是无法还原出原信号的

但现在假定可以，

$y=\Phi \Psi s=As$

压缩感知关注的是如何利用信号本身所具有的稀疏性,从部分观测样本中恢复原信号.

通常认为,压缩感知分为“感知测量”和“重构恢复”这两个阶段.

“感知测量”关注如何对原始信号进行处理以获得稀疏样本表示,这方面的内容涉及傅里叶变换、小波变换以及1字典学习、稀疏编码等,不少技术在压缩感知提出之前就已在信号处理等领域有很多研究;
“重构恢复”关注的是如何基于稀疏性从少量观测中恢复原信号,这是压缩感知的精髓,当我们谈到压缩感知时,通常是指该部分.

“限定等距性”(Restricted Isometry Property,简称RIP):

对大小为n * m的矩阵A，若存在常数δk ∈（0,1）使得任意向量s和A的所有子矩阵Ak∈Rn*k有

则称A满足k限定等距性。通过下面优化近乎完美的从y中恢复出稀疏信号s，进而恢复x:

$L_{0}$ 范数的最小化是一个NP难题， $L_{0}$ 范数最小化在一定条件下与 $L_{0}$ 最小化共解，则：

该式可以转化为LASSO的等价形式通过近端梯度下降求解，即“基寻踪去噪”。