Python(TensorFlow)多模光纤光束算法和GPU并行模拟
🎯要点
🎯多模光纤包含光学系统线性和非线性部分 | 🎯单变量线性回归、多变量线性回归、人脸图像年龄预测、音频语音分类和 X 射线图像评估算法 | 🎯在空间光调制器记录海螺参数矩阵,光束算法多变量预测年龄 | 🎯光束算法数学模型
📜光学和散射用例
🍪语言内容分比


🍇Python光泵浦
光泵浦还用于将原子或分子内束缚的电子循环泵浦至明确的量子态。对于包含单个外壳电子的原子种类的相干两能级光泵浦的最简单情况,这意味着电子被相干泵浦到单个超精细子能级(标记为 m F m_F mF ),这是由泵浦激光器以及量子选择规则。在光泵浦时,据说原子在特定的 m F m_F mF 子能级中定向,然而,由于光泵浦的循环性质,束缚电子实际上会在上能级和下能级之间经历重复的激发和衰变。泵浦激光器的频率和偏振决定了原子取向的 m F m_F mF子能级。
实际上,由于跃迁线宽的功率加宽以及超精细结构捕获和辐射捕获等不良影响,完全相干光泵浦可能不会发生。因此,原子的方向更一般地取决于激光的频率、强度、偏振和光谱带宽以及吸收跃迁的线宽和跃迁概率。
我们首先定义激光束、哈密顿量和磁场。在这里,我们感兴趣的是线偏振光下的 F = 2 → F ′ = 3 F=2 \rightarrow F^{\prime}=3 F=2→F′=3 跃迁。我们制作了三种激光束组合,每种组合都具有沿不同轴的线性偏振。请注意,只有在单激光束的情况下,速率方程和光学布洛赫方程才会一致。这是因为速率方程假设激光是不相干的(它们的电场不会相加得到两倍的振幅),而光学布洛赫方程则假设激光是不相干的。具体来说,两个相干光束使电场加倍,从而使强度四极,因此为了比较速率方程,我们必须乘以 4 。我们对 π y \pi_y πy 和 π z \pi_z πz 极化执行此操作。对于 π x \pi_x πx 光束,我们将其分成两个光束。
最后,可以将失谐置于激光器上或将失谐置于哈密顿量上(或两者的某种组合)。后者似乎更快。
gamma = 1 laserBeams = {}
laserBeams['$\\pi_z$']= pyp.laserBeams([{'kvec': np.array([1., 0., 0.]), 'pol':np.array([0., 0., 1.]),'pol_coord':'cartesian', 'delta':-2.73*gamma, 's':4*0.16*(1+2.73**2)}])
laserBeams['$\\pi_y$']= pyp.laserBeams([{'kvec': np.array([0., 0., 1.]), 'pol':np.array([0., 1., 0.]),'pol_coord':'cartesian', 'delta':-2.73*gamma, 's':4*0.16*(1+2.73**2)}])
laserBeams['$\\pi_x$']= pyp.laserBeams([{'kvec': np.array([0., 0., 1.]), 'pol':np.array([1., 0., 0.]),'pol_coord':'cartesian', 'delta':-2.73*gamma, 's':0.16*(1+2.73**2)},{'kvec': np.array([0., 0., -1.]), 'pol':np.array([1., 0., 0.]),'pol_coord':'cartesian', 'delta':-2.73*gamma, 's':0.16*(1+2.73**2)}])magField = lambda R: np.zeros(R.shape)H_g, muq_g = pyp.hamiltonians.singleF(F=2, gF=1, muB=1)
H_e, mue_q = pyp.hamiltonians.singleF(F=3, gF=1, muB=1)
d_q = pyp.hamiltonians.dqij_two_bare_hyperfine(2, 3)
hamiltonian = pyp.hamiltonian()
hamiltonian.add_H_0_block('g', H_g)
hamiltonian.add_H_0_block('e', H_e-0.*np.eye(H_e.shape[0]))
hamiltonian.add_d_q_block('g', 'e', d_q, gamma=gamma)hamiltonian.print_structure()
计算密度迁移
obe = {}
rateeq = {}
rateeq['$\\pi_z$'] = pyp.rateeq(laserBeams['$\\pi_z$'], magField,hamiltonian)
obe['$\\pi_z$'] = pyp.obe(laserBeams['$\\pi_z$'], magField, hamiltonian,transform_into_re_im=transform)N0 = np.zeros((rateeq['$\\pi_z$'].hamiltonian.n,))
N0[0] = 1
rateeq['$\\pi_z$'].set_initial_pop(N0)
rateeq['$\\pi_z$'].evolve_populations([0, 600/gamma],max_step=1/gamma)rho0 = np.zeros((obe['$\\pi_z$'].hamiltonian.n**2,))
rho0[0] = 1.
obe['$\\pi_z$'].set_initial_rho(np.real(rho0))
obe['$\\pi_z$'].evolve_density(t_span=[0, 600/gamma],progress_bar=True)Neq = rateeq['$\\pi_z$'].equilibrium_populations(np.array([0., 0., 0.]),np.array([0., 0., 0.]), 0.)
绘制结果
fig, ax = plt.subplots(1, 1)
for jj in range(5):ax.plot(gamma*rateeq['$\\pi_z$'].sol.t,rateeq['$\\pi_z$'].sol.y[jj, :], '--',color='C{0:d}'.format(jj),linewidth=1.0)ax.plot(gamma*obe['$\\pi_z$'].sol.t, np.abs(obe['$\\pi_z$'].sol.rho[jj, jj]), '-',color='C{0:d}'.format(jj),linewidth=0.5)ax.plot(gamma*obe['$\\pi_z$'].sol.t[-1], Neq[jj], '.', color='C{0:d}'.format(jj),linewidth=0.5)ax.set_xlabel('$\\Gamma t$')
ax.set_ylabel('$\\rho_{ii}$');
接下来,我们要检查我们的旋转是否正常工作,因此我们将对具有 π y \pi_y πy 偏振的 z ^ \hat{z} z^ 行进光束进行相同的计算。但在我们使用光学布洛赫方程之前,我们需要首先创建初始状态,这涉及到旋转我们的状态。
mug = spherical2cart(muq_g)
S = -mugE, U = np.linalg.eig(S[1])
inds = np.argsort(E)
E = E[inds]
U = U[:, inds]
Uinv = np.linalg.inv(U)
psi = U[:, 0]rho0 = np.zeros((hamiltonian.n, hamiltonian.n), dtype='complex128')
for ii in range(hamiltonian.ns[0]):for jj in range(hamiltonian.ns[0]):rho0[ii, jj] = psi[ii]*np.conjugate(psi[jj])obe['$\\pi_y$'] = pyp.obe(laserBeams['$\\pi_y$'], magField, hamiltonian,transform_into_re_im=transform)
obe['$\\pi_y$'].set_initial_rho(rho0.reshape(hamiltonian.n**2,))
obe['$\\pi_y$'].evolve_density(t_span=[0, 600],progress_bar=True)for jj in range(obe['$\\pi_y$'].sol.t.size):obe['$\\pi_y$'].sol.rho[:5, :5, jj] = Uinv@obe['$\\pi_y$'].sol.rho[:5, :5, jj]
绘制结果
fig, ax = plt.subplots(1, 1)
for jj in range(5):ax.plot(obe['$\\pi_y$'].sol.t,np.abs(obe['$\\pi_y$'].sol.rho[jj, jj]), '-',color='C{0:d}'.format(jj),linewidth=0.5)
ax.set_xlabel('$\\Gamma t$')
ax.set_ylabel('$\\rho_{ii}$');
现在,让我们对 π x \pi_x πx 做同样的事情,只不过这次我们有两束激光束,强度为 1 / 4 1 / 4 1/4:
E, U = np.linalg.eig(S[0])inds = np.argsort(E)
E = E[inds]
U = U[:, inds]
Uinv = np.linalg.inv(U)psi = U[:, 0]rho0 = np.zeros((hamiltonian.n, hamiltonian.n), dtype='complex128')
for ii in range(hamiltonian.ns[0]):for jj in range(hamiltonian.ns[0]):rho0[ii, jj] = psi[ii]*np.conjugate(psi[jj])obe['$\\pi_x$'] = pyp.obe(laserBeams['$\\pi_x$'], magField, hamiltonian,transform_into_re_im=transform)
obe['$\\pi_x$'].set_initial_rho(rho0.reshape(hamiltonian.n**2,))
obe['$\\pi_x$'].evolve_density(t_span=[0, 600],progress_bar=True)for jj in range(obe['$\\pi_x$'].sol.t.size):obe['$\\pi_x$'].sol.rho[:5, :5, jj] = Uinv@obe['$\\pi_x$'].sol.rho[:5, :5, jj]
👉参阅、更新:计算思维 | 亚图跨际
相关文章:

Python(TensorFlow)多模光纤光束算法和GPU并行模拟
🎯要点 🎯多模光纤包含光学系统线性和非线性部分 | 🎯单变量线性回归、多变量线性回归、人脸图像年龄预测、音频语音分类和 X 射线图像评估算法 | 🎯在空间光调制器记录海螺参数矩阵,光束算法多变量预测年龄 | &#…...

实战Kubernetes之快速部署 K8s 集群 v1.28.0
文章目录 一、前言二、主机准备三、系统配置3.1. 关闭防火墙及相关配置3.2. 修改主机名3.3. 主机名DNS解析3.4. 时间同步3.5. 配置网络3.6. 重启服务器 四、安装软件4.1. 安装 Docker4.2. 安装 cri-dockerd4.3. 添加国内YUM源4.4. 安装 kubeadm、kubelet 和 kubectl 五、Master…...

YOLO知识点总结:
分类: 即是将图像结构化为某一类别的信息,用事先确定好的类别(category)或实例ID来描述图片。这一任务是最简单、最基础的图像理解任务,也是深度学习模型最先取得突破和实现大规模应用的任务。其中,ImageNet是最权威的评测集&…...

合宙LuatOS AIR700 IPV6 TCP 客户端向NodeRed发送数据
为了验证 AIR700 IPV6 ,特别新建向NodeRed Tcp发送的工程。 Air700发送TCP数据源码如下: --[[ IPv6客户端演示, 仅EC618系列支持, 例如Air780E/Air600E/Air780UG/Air700E ]]-- LuaTools需要PROJECT和VERSION这两个信息 PROJECT "IPV6_SendDate_N…...

git 如何生成sshkey公钥
打开git客户端 输入 ssh-keygen -t rsa -b 4096 -C "xxxxxxexample.com" 然后根据提示按enter 或者y 直到出现下图所示 打开 c盘的路径下的文件,/c/Users/18159/.ssh/id_rsa.pub 将id_rsa.pub中的公钥贴到git 网站上的SSH keys即可...

python从入门到精通:函数
目录 1、函数介绍 2、函数的定义 3、函数的传入参数 4、函数的返回值 5、函数说明文档 6、函数的嵌套调用 7、变量的作用域 1、函数介绍 函数是组织好的,可重复使用的,用来实现特定功能的代码段。 name "zhangsan"; length len(nam…...

【Android性能篇】如何分析 dumpsys meminfo 信息
一、dumpsys meminfo是什么 dumpsys meminfo 是一个用于分析Android设备内存使用情况的强大命令。 二、dumpsys meminfo的关键信息 要分析其输出信息,我们需要注意以下几个关键点: Total PSS by OOM adjustment:这个值表示每个进程的总比…...

c++进阶——继承的定义,复杂的菱形继承及菱形虚拟继承
目录 前言: 1.继承的概念及定义 1.1继承的概念 1.2 继承定义 1.2.2继承关系和访问限定符 1.2.3继承基类成员访问方式的变化 2.基类和派生类对象赋值转换 3.继承中的作用域 4.派生类的默认成员函数 5.继承与友元 6. 继承与静态成员 7.复杂的菱形继承及菱…...

计算机网络:DNS、子网掩码、网关
参考: https://blog.csdn.net/weixin_55255438/article/details/123074896 https://zhuanlan.zhihu.com/p/65226634 在计算机网络中,DNS(Domain Name System,域名系统)、子网掩码(Subnet Mask)…...

程序员如何学习开源项目
程序员如何学习开源项目 豆包MarsCode使用豆包MarsCode学习开源项目步骤导入git上开源的项目 豆包MarsCode https://www.marscode.cn/home 使用豆包MarsCode学习开源项目 步骤 https://www.marscode.cn/dashboard 导入git上开源的项目 找到项目的README.md文件,使…...
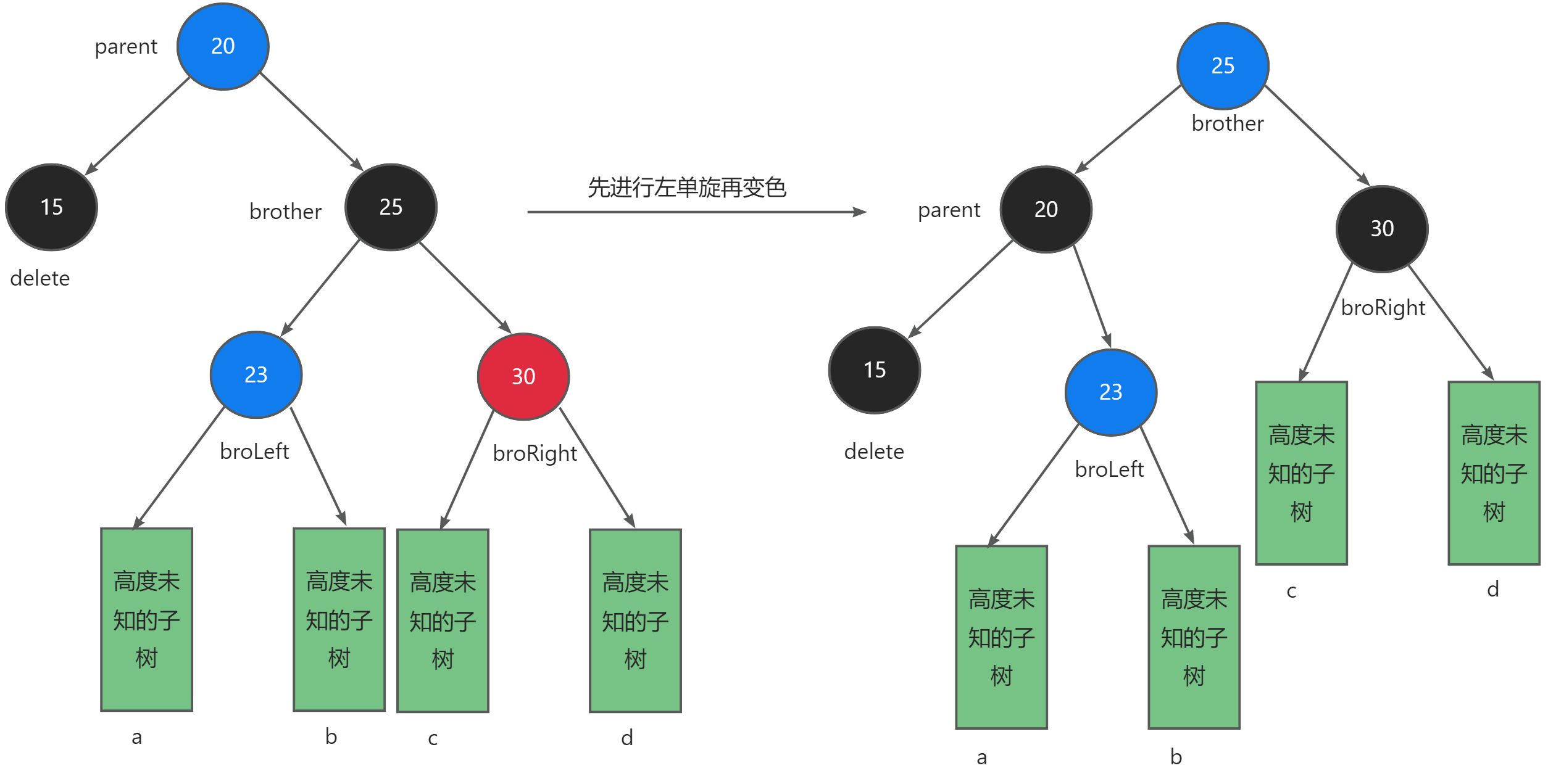
探索数据结构:红黑树的分析与实现
✨✨ 欢迎大家来到贝蒂大讲堂✨✨ 🎈🎈养成好习惯,先赞后看哦~🎈🎈 所属专栏:数据结构与算法 贝蒂的主页:Betty’s blog 1. 红黑树的介绍 1.1. 红黑树的引入 我们前面学习了AVL树,…...

【设计模式】装饰器模式和适配模式
装饰器模式 装饰器模式能够很好的对已有功能进行拓展,这样不会更改原有的代码,对其他的业务产生影响,这方便我们在较少的改动下对软件功能进行拓展。 类似于 router 的前置守卫和后置守卫。 Function.prototype.before function (beforeFn)…...
Visual Studio VS 插件之 ReSharper
集成在VS2022上的ReSharper暂无找到汉化方式,如果有大神可以汉化,请指导下。 首先ReSharper 是IDE 下的插件 主要是基于C# 语句优化的这么一个插件。 使用ReSharper可以使开发效率大大提高,但是也是比较吃电脑的配置。所以说如果配置低的小…...

【二分查找】--- 进阶题目赏析
Welcome to 9ilks Code World (๑•́ ₃ •̀๑) 个人主页: 9ilk (๑•́ ₃ •̀๑) 文章专栏: 算法Journey 本篇博客我们继续来了解一些有关二分查找算法的进阶题目。 🏠 寻找峰值 📌 题目内容 162. 寻找峰值 - 力扣&#…...

CSS 对齐
CSS 对齐 在网页设计中,CSS(层叠样式表)对齐是一种基本而重要的技术,它决定了网页元素的位置和布局。CSS 提供了多种对齐方法,可以精确控制元素的水平、垂直对齐,以及相对于其父元素或整个页面的位置。本文…...

暑假算法刷题日记 Day 10
目录 重点整理 054、 拼数 题目描述 输入格式 输出格式 输入输出样例 核心思路 代码 055、 求第k小的数 题目描述 输入格式 输出格式 输入输出样例 核心思路 代码 总结 这几天我们主要刷了洛谷上排序算法对应的一些题目,相对来说比较简单 一共是13道…...

【Midjourney】AI作画提示词工程:精细化技巧与高效实践指南
文章目录 💯AI作画提示词基础结构1 图片链接1.1 上传流程 2 文字描述3 后置参数 💯AI作画提示词的文字描述结构1 主体主体细节描述2 环境背景2.1 环境2.2 光线2.3 色彩2.4 氛围 3 视角4 景别构图5 艺术风格6 图片制作方法7 作品质量万能词 💯…...

C语言——文件
文件操作 概念 文件是指存储在外存储器上(一般代指磁盘,也可以是U盘,移动硬盘等)的数据的集合。 文件操作体现在哪几个方面 1.文件内容的读取 2.文件内容的写入 数据的读取和写入可被视为针对文件进行输入和输出的操作…...

视频孪生技术在智慧水利(水务)场景中的典型应用展示
一、智慧水利建设规划 根据水利部编制《“十四五”智慧水利建设规划》,建设数字孪生流域、“2N”水利智能业务应用体系、安全可控水利网络安全防护体系、优化健全水利网信保障体系,建成七大江河数字孪生流域,推进水利工程智能化改造…...

使用kubekey快速搭建k8s集群
项目仓库地址 https://github.com/kubesphere/kubekey/ 支持的Kubernetes Versions https://github.com/kubesphere/kubekey/blob/master/docs/kubernetes-versions.md 安装 选择自己想要下载的版本 https://github.com/kubesphere/kubekey/releases 复制下载链接并下载 示…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
