机器学习-混淆矩阵
文章目录
- 一、混淆矩阵
- 1.混淆矩阵简介
- 2.混淆矩阵图列
- 二、混淆矩阵指标
- 1. 准确率(Accuracy)
- 2. 精确率(Precision)
- 3. 召回率(Recall)
- 4. F1分数(F1 Score)
- 三、总结
一、混淆矩阵
1.混淆矩阵简介
随着机器学习和人工智能的迅速发展,分类模型成为了解决各种问题的重要工具。然而,仅仅知道模型预测对了多少样本是不够的。我们需要一种更详细、更系统的方法来理解模型的分类能力,以及它在不同类别上的表现。
混淆矩阵是机器学习中一种评估分类模型性能的工具,特别是在监督学习中。它主要用于描述分类模型的预测结果与实际样本类别之间的关系。混淆矩阵通过矩阵的形式,展示了每个类别中预测正确的样本数和预测错误的样本数。
2.混淆矩阵图列
混淆矩阵的行代表样本的真实类别,列代表模型预测的类别。对于一个二分类问题(假设为类别0和类别1),混淆矩阵如下所示:
| 预测为0 | 预测为1 | |
|---|---|---|
| 真实0 | TN(真负类) | FP(假正类) |
| 真实1 | FN(假负类) | TP(真正类) |
其中:
- 真正类(True Positives, TP):模型正确地将正类预测为正类的数量。
- 假负类(False Negatives, FN):模型错误地将正类预测为负类的数量。
- 假正类(False Positives, FP):模型错误地将负类预测为正类的数量。
- 真负类(True Negatives, TN):模型正确地将负类预测为负类的数量。
对于多分类问题,混淆矩阵会扩展为更多的行和列,每行每列分别对应一个类别。
二、混淆矩阵指标
基于混淆矩阵,我们可以计算出多种评估指标,如准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1值(F1 Score)等,这些指标可以更加全面地评估模型的性能,有助于我们根据具体需求调整和优化模型。
1. 准确率(Accuracy)
含义:准确率是指模型正确分类的样本数占总样本数的比例。它衡量了模型整体的分类能力,但在类别不平衡的数据集上可能具有误导性。
计算公式:
A c c u r a c y = ( T P + T N ) / ( F P + F N + T P + T N ) Accuracy= (TP+TN) /(FP+FN+TP+TN) Accuracy=(TP+TN)/(FP+FN+TP+TN)
其中,TP表示真正例,TN表示真负例,FP表示假正例,FN表示假负例。
2. 精确率(Precision)
含义:精确率(也称为查准率)是指模型预测为正类的样本中,实际为正类的样本比例。它衡量了模型预测为正类的可靠性。
计算公式:
P r e c i s i o n = T P / ( F P + T P ) Precision= TP/ (FP+TP) Precision=TP/(FP+TP)
精确率高意味着模型在预测为正类的结果中,大部分是正确的。
3. 召回率(Recall)
含义:召回率(也称为查全率)是指实际为正类的样本中,被模型正确预测为正类的样本比例。它衡量了模型对正类样本的识别能力。
计算公式:
R e c a l l = T P / ( F N + T P ) Recall= TP/(FN+TP) Recall=TP/(FN+TP)
召回率高意味着模型能够捕捉到更多的正类实例。
4. F1分数(F1 Score)
含义:F1分数是精确率和召回率的调和平均数,用于综合评估模型的性能。它平衡了精确率和召回率的重要性,提供了一个单一的评估指标。
计算公式:
F 1 S c o r e = ( 2 × P r e c i s i o n × R e c a l l ) / ( P r e c i s i o n + R e c a l l ) F1 Score= (2×Precision×Recall)/ (Precision+Recall) F1Score=(2×Precision×Recall)/(Precision+Recall)
F1分数的取值范围为0到1,值越接近1表示模型的预测性能越好。
三、总结
这四个指标在评估分类模型时各有侧重,准确率衡量了模型的整体分类能力,精确率衡量了模型预测为正类的可靠性,召回率衡量了模型对正类样本的识别能力,而F1分数则综合了精确率和召回率,提供了一个更为全面的评估视角。在实际应用中,可以根据具体需求和数据特性选择合适的评估指标。
相关文章:

机器学习-混淆矩阵
文章目录 一、混淆矩阵1.混淆矩阵简介2.混淆矩阵图列 二、混淆矩阵指标1. 准确率(Accuracy)2. 精确率(Precision)3. 召回率(Recall)4. F1分数(F1 Score) 三、总结 一、混淆矩阵 1.混…...

数据结构----栈
一丶概念 只能在一端进行插入和删除操作的线性表(又称为堆栈),进行插入和删除操作的一端称为栈顶,另一端称为栈底 二丶特点 先进后出 FILO first in last out 后进先出 LIFO last in first out 三丶顺序栈 逻辑结构&…...

STL六大组件
STL(Standard Template Library,标准模板库)是C标准库的一部分,提供了丰富且高效的数据结构和算法。STL主要由6大组件构成,分别是容器、算法、迭代器、适配器、仿函数和空间配置器。 容器(Containers&#…...

【机器学习】CNN的数学基础
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 CNN的数学基础1. 引言2. 卷积运算2.1 连续卷积2.2 离散卷积2.3 互相关 3. 激活函…...

最小路径和[中等]
优质博文:IT-BLOG-CN 一、题目 给定一个包含非负整数的m x n网格grid,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。 说明:每次只能向下或者向右移动一步。 示例 1: 输入:grid [[…...

【题库】——数组 小鱼比可爱
#include<bits/stdc.h> using namespace std; int main() {int n,m,i;cin>>n;int arr[n]; for(i0;i<n;i) {int count 0;cin>>arr[i];for(mi;m>0;m--){if(arr[i]>arr[m])count;} cout<<count<<" "; } return 0; }...
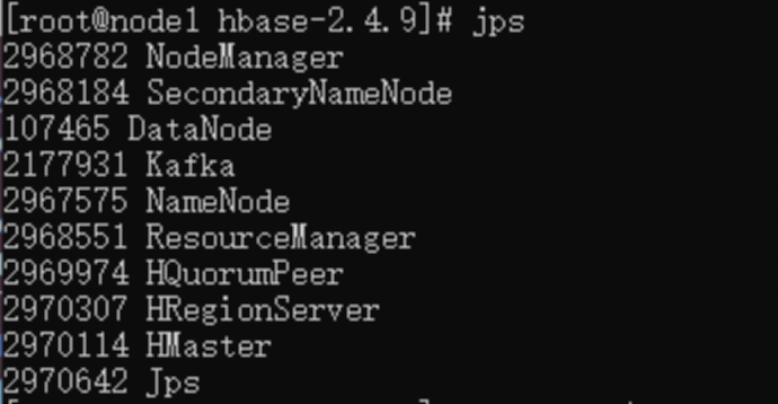
基于飞腾平台的Hbase的安装配置
【写在前面】 飞腾开发者平台是基于飞腾自身强大的技术基础和开放能力,聚合行业内优秀资源而打造的。该平台覆盖了操作系统、算法、数据库、安全、平台工具、虚拟化、存储、网络、固件等多个前沿技术领域,包含了应用使能套件、软件仓库、软件支持、软件适…...

【springboot】springboot接口参数全局解密,解决request内容修改后如何重新设置回去的问题
文章目录 核心思路spring&servelt基础核心接口类核心代码 body解密核心原理讲解get解密核心原理讲解get query请求讲解get pathVariables请求讲解 总结 本文不仅介绍了body内容修改后如何传递,也介绍了get请求 在修改内容后如何继续传递。 【原创作者 csdn: 孟秋…...

yml基本语法
YAML(YAML Ain’t Markup Language)是一种简洁且易读的数据序列化格式,常用于配置文件。Spring Boot 中的 application.yml 文件使用 YAML 来配置应用程序的属性。 YAML 基本语法 1. 键值对 基本的键值对表示形式为:key: value…...
橙色简洁大气体育直播自适应模板赛事直播门户自适应网站源码
源码名称:酷黑简洁大气体育直播自适应模板赛事直播门户网站 源码开发环境:帝国cms 7.5 安装环境:phpmysql 带采集,可以挂着电脑上自动采集发布,无需人工操作! 橙色简洁大气体育直播自适应模板赛事直播门户…...

【启明智显技术分享】工业级HMI芯片Model系列GUI合成到项目中的指南
在工业自动化、智能终端HMI、车载仪表盘等领域,高性能的HMI(人机界面)芯片是不可或缺的核心组件。启明智显推出的Model系列(如Model3C、Model3、Model4)HMI芯片,以其卓越的性能和广泛的应用领域,…...

开源服务器运维工具1Panel
1Panel是杭州飞致云信息科技有限公司推出的一款现代化、开源的Linux服务器运维管理面板。 以下是对1Panel的详细介绍: 一、基本信息 产品名称:1Panel所属公司:杭州飞致云信息科技有限公司编写语言:Golang上线时间:20…...

新版本源2.0大模型发布:Yuan2-2B-July-hf
引言 近日,浪潮信息的新一代基础语言大模型源2.0 迎来了重要更新。浪潮信息正式发布了 Yuan2-2B-July-hf 模型,标志着源2.0系列模型在性能和功能上的进一步提升。这一版本将为开发者和研究人员提供更强大的工具,以满足各种语言处理需求。…...
用python生成GIF动图—用于博客插图或封面等
生成GIF动图🚀 由于目前自己是在做大模型,还有一些树莓派硬件之类的东西,一是大模型的流式输出的例子需要用到GIF,二是做单片机的时候例如一些灯的闪烁和变化需要用到,所以之前也是一直有这个打算所以就记录一下这个生…...

[RCTF2019]draw
下载是一个文本文档,百度AI cs pu lt 90 fd 500 rt 90 pd fd 100 rt 90 repeat 18[fd 5 rt 10] lt 135 fd 50 lt 135 pu bk 100 pd setcolor pick [ red orange yellow green blue violet ] repeat 18[fd 5 rt 10] rt 90 fd 60 rt 90 bk 30 rt 90 fd 60 pu lt 90 f…...

设计模式 - 责任链模式
💝💝💝首先,欢迎各位来到我的博客!本文深入理解设计模式原理、应用技巧、强调实战操作,提供代码示例和解决方案,适合有一定编程基础并希望提升设计能力的开发者,帮助读者快速掌握并灵活运用设计模式。 💝💝💝如有需要请大家订阅我的专栏【设计模式】哟!我会定…...

jpg怎么转换成pdf?6个简单方法,实现jpg转换成pdf
你是否也曾想将jpg图片转换为pdf格式文档呢?亦或者在处理文档或制作报告时,不知道怎么才能更快地将多张图片整合成一个pdf文件呢?如果你正在寻找简单快速的方法,又有哪些工具可以帮助您完成图片转pdf呢?别着急…...

ptrade排坑笔记——使用量化交易的时候有报错提示!
前言 今天要和大家分享一个遇见的问题,有客户反馈,自己在使用量化交易的时候,会有报错!会在后文分享我们是如何解决这个问腿的! 一、问题描述 客户主要遇见的问题是,量化在进行交易的过程中,…...

C#-MemoryMarshal
MemoryMarshal 类是 .NET 中用于处理内存的工具类,它提供了一组静态方法,用于在托管代码中以安全和高效的方式操作内存块。MemoryMarshal 类主要用于处理原始内存数据而不需要进行复制,这对于性能关键的操作非常有用。 MemoryMarshal 类包含…...

Java并发编程的艺术
Java作为一门面向对象的编程语言,自1995年推出以来,一直以其稳定性、跨平台性和丰富的API受到广大开发者的喜爱。在Java的发展历程中,并发编程一直是其重要的特性之一。本文将探讨Java并发编程的艺术,解析其核心概念和常用并发工具…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...
