机器学习:朴素贝叶斯模型算法原理(含实战案例)
机器学习:朴素贝叶斯模型算法原理
作者:i阿极
作者简介:Python领域新星作者、多项比赛获奖者:博主个人首页
😊😊😊如果觉得文章不错或能帮助到你学习,可以点赞👍收藏📁评论📒+关注哦!👍👍👍
📜📜📜如果有小伙伴需要数据集和学习交流,文章下方有交流学习区!一起学习进步!💪
| 专栏案例:机器学习 |
|---|
| 机器学习:基于逻辑回归对某银行客户违约预测分析 |
| 机器学习:学习k-近邻(KNN)模型建立、使用和评价 |
| 机器学习:基于支持向量机(SVM)进行人脸识别预测 |
| 决策树算法分析天气、周末和促销活动对销量的影响 |
| 机器学习:线性回归分析女性身高与体重之间的关系 |
| 机器学习:基于主成分分析(PCA)对数据降维 |
| 机器学习:基于朴素贝叶斯对花瓣花萼的宽度和长度分类预测 |
| 机器学习:学习KMeans算法,了解模型创建、使用模型及模型评价 |
| 机器学习:基于神经网络对用户评论情感分析预测 |
文章目录
- 机器学习:朴素贝叶斯模型算法原理
- 1、前言
- 2、实验原理
- 2.1、一维特征向量
- 2.2二维特征向量
- 2.3n维特征向量
- 3、朴素贝叶斯模型演示
- 4、案例实战:肿瘤预测
- 4.1案例背景
- 4.2读取数据
- 4.3划分特征变量和目标变量
- 4.4划分训练集和测试集
- 4.5高斯朴素贝叶斯模型
- 4.6模型预测
- 总结
1、前言
随着人工智能的不断发展,机器学习这门技术也越来越重要,很多人都开启了学习机器学习,本文就介绍了机器学习的基础内容。
在这个信息爆炸的时代,如何高效处理数据并利用数据推动决策显得尤为重要,这便是人们通常所说的“数据分析”。与数据分析相伴而生的机器学习(Machine Learning),有些人可能会感到陌生,然而说到战胜了众多人类围棋高手的智能机器人AlphaGo,想必大多数人都有所耳闻。AlphaGo背后的原理支撑就是机器学习,它通过模拟人类的学习行为,不停地分析海量的围棋数据,发现数据背后的规律,从而在已有条件下做出最为理性的决断,这个过程充满了机器美学。
Python是数据分析和机器学习的一把“利刃”,其功能强大且简单易上手。
2、实验原理
贝叶斯分类是机器学习中应用极为广泛的分类算法之一,其产生来自于贝叶斯对于逆概问题的思考,朴素贝叶斯是贝叶斯模型当中最简单的一种。
其算法核心为贝叶斯公式:
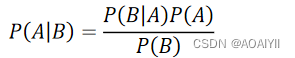
P(A)为事件A发生的概率
P(B)为事件B发生的概率
P(A|B)表示在事件B发生的条件下事件A发生的概率
同理P(B|A)则表示在事件A发生的条件下事件B发生的概率
如果只看公式,有些小伙伴会无法快速知道其中原理。举个例子:
已知流感季节一个人感冒(事件A)的概率为40%(P(A))
一个人打喷嚏(事件B)的概率为80%(P(B))
一个人感冒的条件下打喷嚏的概率为100%(P(B|A))
求这个人在打喷嚏的条件下患感冒的概率P(A|B),求解过程如下图所示:
2.1、一维特征向量
首先以一个更详细的例子来讲解一下贝叶斯公式更加偏实战的应用:如何判断一个人是否感冒了。假设已经有5个样本数据,如下表所示:
| 打喷嚏(X) | 感冒(Y) |
|---|---|
| 1 | 1 |
| 1 | 1 |
| 0 | 1 |
| 1 | 1 |
| 1 | 0 |
打喷嚏 (X):其中数字1表示打喷嚏,0表示不打喷嚏;
感冒 (Y):其中数字1表示感冒了,数字0表示未感冒。
我们要利用贝叶斯公式,一个人打喷嚏 (X=1),那么他是否感冒了呢,也即预测他处于感冒状态的概率为多少,我们把此概率写作P(Y|X)。
则贝叶斯公式就有:
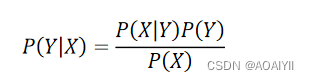
根据上述数据,我们可以计算在打喷嚏 (X=1) 的条件下,患上感冒的概率为:
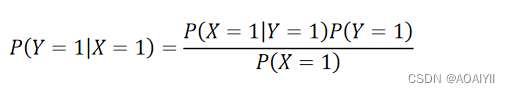
再根据上面的公式,代入数据得:
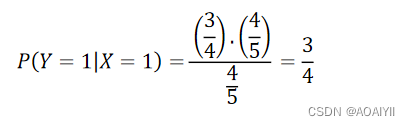
2.2二维特征向量
在上面,我们讲解了一维特征向量,只有两个变量。现在来讲二维特征向量,加入另外一个特征变量:头痛(X),其中数字1表示头痛,0表示不头痛;这里的目标变量仍为感冒(Y)。
| 打喷嚏(X1) | 头痛(X2) | 感冒(Y) |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 1 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
一个人他打喷嚏且头痛 (X1=1, X2=1) ,那么他是否感冒了呢,也即预测他处于感冒状态的概率为多少,在数学上,我们把此概率写作P(Y|X1,X2)。
则贝叶斯公式就有:
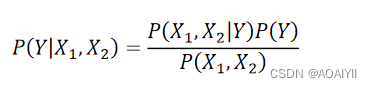
在比较 P(Y=1|X1,X2) 与 P(Y=0|X1,X2) 时,由于分母 P(X1,X2) 的值是相同的,所以我们在实际计算中可以舍去这部分的计算,直接比较两者分子大小即可。即:
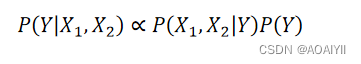
2.3n维特征向量
我们可以在2个特征变量的基础上推广至n个特征变量 X1, X2, … , Xn,应用贝叶斯公式有:
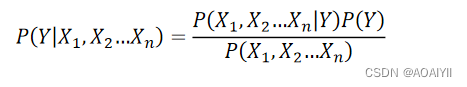
朴素贝叶斯模型假设给定目标值后特征之间相互独立,上式可以写作:
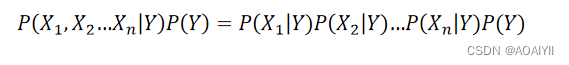
3、朴素贝叶斯模型演示
朴素贝叶斯模型(这里用的是高斯贝叶斯分类器)的引入方式如下所示:
导入模块
from sklearn.naive_bayes import GaussianNB
创建相关数据
X = [[1, 2], [3, 4], [5, 6], [7, 8], [9, 10]]
y = [0, 0, 0, 1, 1]
建立高斯贝叶斯分类器
model = GaussianNB()
model.fit(X, y)
使用模型对数据预测
print(model.predict([[6,6]]))
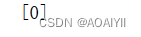
4、案例实战:肿瘤预测
4.1案例背景
医疗水平突飞猛进,人们对医院快速识别肿瘤是否为良性的要求同样也越来越高,能否根据患者肿瘤的相关特征水平快速判断肿瘤的性质影响着患者的治疗方式和痊愈速度。传统的做法是医生根据数十个指标来判断肿瘤的性质,不过该方法的预测效果依赖于医生的个人经验而且效率较低,而通过机器学习我们有望能快速预测肿瘤的性质。
4.2读取数据
import pandas as pd
df = pd.read_excel(r"D:\CSDN\data\naivebayes\肿瘤数据.xlsx")
df.head()
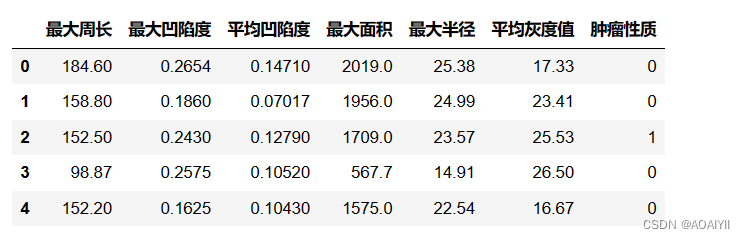
最大周长,最大凹陷度,最大面积,最大半径代表所有肿瘤中最大3个值的平均值
平均凹陷度,平均表面纹理灰度值,代表所有肿瘤度的平均值
对于目标变量肿瘤性质,Y=0 代表肿瘤为恶性,Y=1代表肿瘤为良性
4.3划分特征变量和目标变量
将特征变量和目标变量单独提取出来
X = df.drop(columns='肿瘤性质')
y = df['肿瘤性质']
4.4划分训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
4.5高斯朴素贝叶斯模型
from sklearn.naive_bayes import GaussianNB
nb_clf = GaussianNB()
nb_clf.fit(X_train,y_train)
nb_clf.score(X_train,y_train)
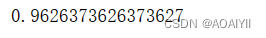
4.6模型预测
搭建模型的目的便是希望利用它来预测数据,这里把测试集中的数据导入到模型中来进行预测,代码如下,其中nb_clf就是上面搭建的朴素贝叶斯回归模型。
pre = nb_clf.predict(X_test)
利用创建DataFrame相关知识点,将预测的y_pred和测试集实际的y_test汇总,代码如下:
data = pd.DataFrame()
data['预测值'] = list(pre)
data['实际值'] = list(y_test)
查看测试集数据对预测准确度
from sklearn.metrics import accuracy_score
score = accuracy_score(pre,y_test)
score
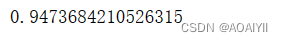
将score打印输出,发现score的值为0.947,也即预测准确度为94.7%,说明114(569*0.2)个测试数据中,共有约108个数据预测正确,6个数据预测错误。
总结
朴素贝叶斯模型是一种非常经典的机器学习模型,它主要基于贝叶斯公式,在应用过程中会把数据集中的特征看成是相互独立的,而不需考虑特征间的关联关系,因此运算速度较快。相比于其他经典的机器学习模型,朴素贝叶斯模型的泛化能力稍弱,不过当样本及特征的数量增加时,其预测效果也是不错的。
相关文章:
机器学习:朴素贝叶斯模型算法原理(含实战案例)
机器学习:朴素贝叶斯模型算法原理 作者:i阿极 作者简介:Python领域新星作者、多项比赛获奖者:博主个人首页 😊😊😊如果觉得文章不错或能帮助到你学习,可以点赞👍收藏&…...

Linux 多线程:理解线程
目录一、理解线程的思想二、Linux中的线程与进程1.Linux中的进程2.Linux中的线程三、线程的工作方式四、线程的独有数据与共享数据1.独有数据2.共享数据一、理解线程的思想 线程就是把一个进程分成多个执行部分,一个部分就是一个线程,比如可以让一个线程…...
Web前端学习:章四 -- JavaScript初级(四)-- BOM
138:Object数据格式简介 1、object对象 JS中独有 的一种数据格式 名字可以随便取,值一般就那几种数据格式 139:BOM - JS跳转页面 BOM Browser Object Model:浏览器对象模型 使用JavaScript控制浏览器交互 控制浏览器里面的内…...

Lesson9.网络基础1
网络协议初识 所谓的协议就是人们为了通信的一种约定 操作系统要进行协议管理,必然会先描述,再组织协议本质就是软件,软件是可以"分层"协议在设计的时候,就是被层状的划分的, 为什么要划分成为层状结构 场景复杂功能解耦(便于人们进行各种维护)OSI七层模型 局域网中…...
这几个SQL语法的坑,你踩过吗
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址:https://github.com/…...

算法基础——复杂度
前言 算法是解决问题的一系列操作的集合。著名的计算机科学家Niklaus Wirth曾提出:算法数据结构程序,由此可见算法在编程中的重要地位。本篇主要讨论算法性能好坏的标准之一——复杂度。 1 复杂度概述 1.1 什么是复杂度 本文所讨论的复杂度是指通过事先…...

基类与派生类对象的关系 派生类的构造函数
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章,「初学」C 🔥座右铭:“不要等到什么都没有了,才下…...
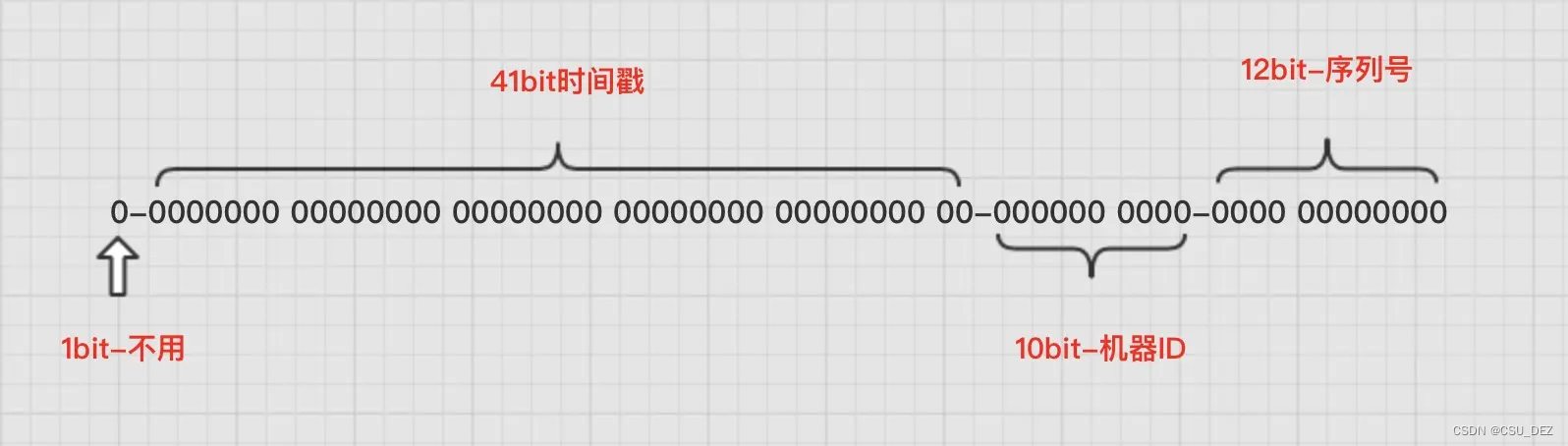
【算法】生成分布式 ID 的雪花算法
ID 是数据的唯一、不变且不重复的标识,在查询数据库的数据时必须通过 ID 查询,在分布式环境下生成全局唯一的 ID 是一个重要问题。 雪花算法(snowflake)是一种生成分布式环境下全局唯一 ID 的算法,该算法由 Twitter 发…...
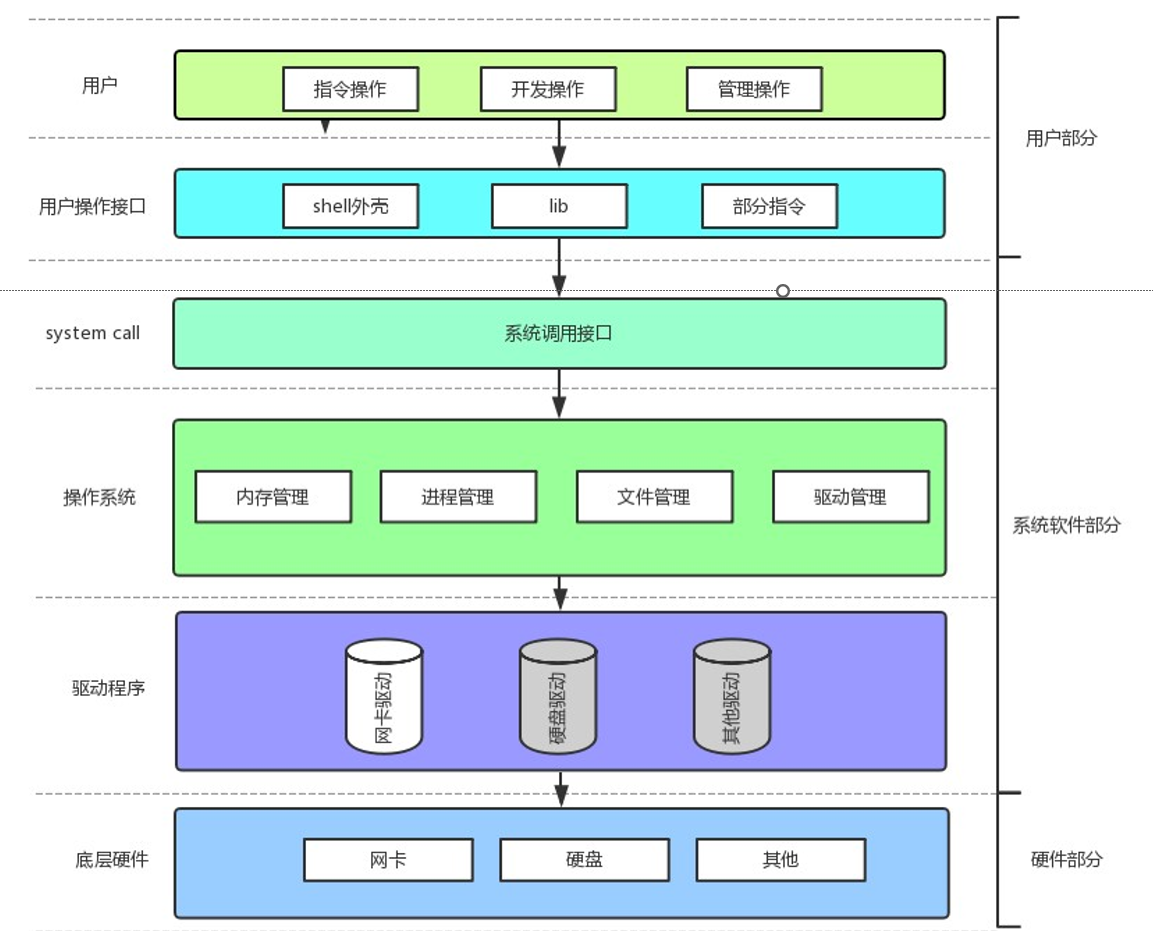
Linux系统编程 - 基础IO(IO操作)
目录 预备知识 复习C文件IO相关操作 printf相关函数 fprintf snprintf 读取文件 系统文件IO操作 open函数 umask()函数 open函数返回值 预备知识 1.你真的理解文件原理和操作了吗?不是语言问题,是系统问题2.是不是只有C/C有文件操作呢&#x…...

基于 Avue 的 CRUD 表格组件封装
在 components 文件夹中,创建一个新的 .vue 文件,例如:AvueCrudTable.vue。 透传父组件传递的属性和事件 : 1、利用v-bind=“ a t t r s " 支持所有 a v u e 的使用方法并在其基础上进行封装 2 、使用 v − o n = " attrs"支持所有 avue 的使用方法并在其基…...
基于框架编写驱动代码)
树莓派学习笔记(十三)基于框架编写驱动代码
文章目录一、代码分析:二、源码一、代码分析: 在内核中由于代码文件多,避免函数名重复,使用static将函数的作用域限制在该文件内 内核的打印函数printk和printf类似 file_operations结构体使用符号“ . ”指定参数,省…...
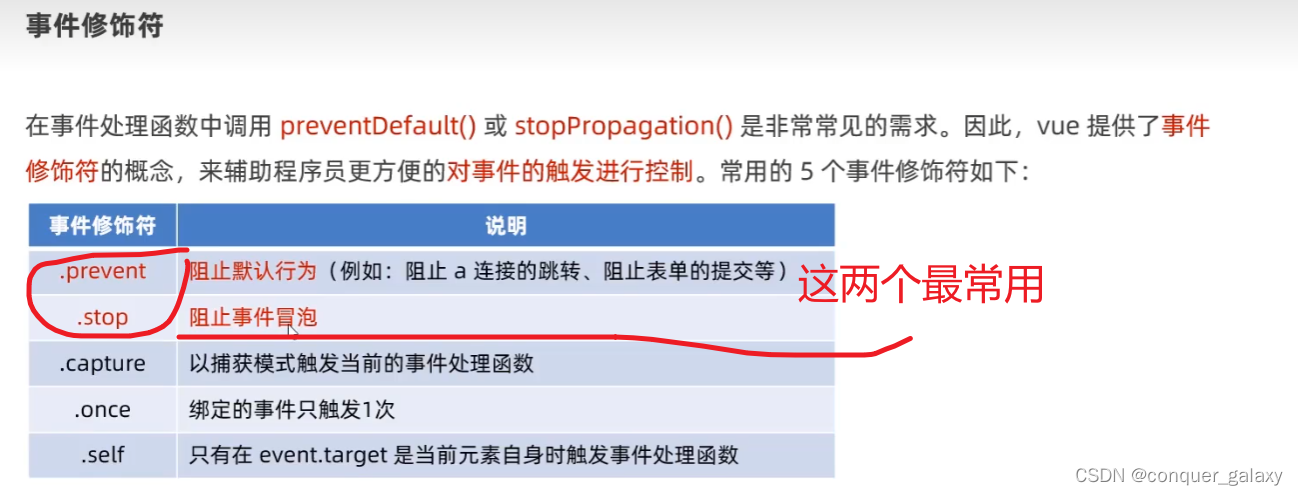
vue事件修饰符之.prevent
.prevent 事件修饰符只是阻止默认事件,不会自动触发任何事件处理函数。因此,在使用 .prevent 事件修饰符时,需要自己编写相应的事件处理函数来处理事件。 例如,在上面的例子中,我们通过在表单上绑定 submit.prevent&q…...

【SpringCloud AlibabaSentinel实现熔断与限流】
本笔记内容为尚硅谷SpringCloud AlibabaSentinel部分 目录 一、Sentinel 1、官网 2、Sentinel是什么 3、下载 4、特性 5、使用 二、安装Sentinel控制台 1、sentinel组件由2部分构成 2、安装步骤 1.下载 2.运行命令 3.访问sentinel管理界面 三、初始化演示工程 …...

类与对象-封装
一、封装的意义封装是C面向对象三大特性之一语法: class name { 访问权限:属性行为 };注意:类中的属性和行为 统称为成员属性 又称 成员属性 / 成员变量行为 又称 成员函数 / 成员方法封装将属性和行为作为一个整体,表现生活中的事物例①&…...

【回忆杀】2012年拥有第一台电脑【致逝去的青春】
高中说起 在2012年的时候吧,高考过后,那个时候一门心思的想当一名体育老师【现在居然还有这个想法,哈哈】,最后没有考上自己希望的大学我记得好像是2012年7月的时候就去重庆投靠朋友,他教我做模具,2012年做…...

PointNeXt: Revisiting PointNet++ with Improved Training and Scaling Strategies
Abstract PointNet 是点云理解领域最有影响力的神经网络架构之一。虽然近期出现了 PointMLP 和 Point Transformer 等新型网络,它们的精度已经大大超过了 PointNet,但我们发现大部分性能提升是由于改进的训练策略,例如数据增强和优化技术以及…...
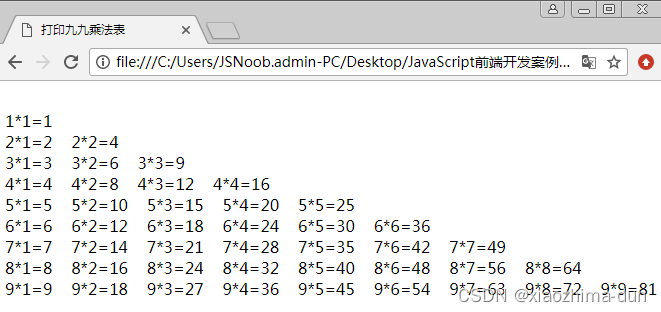
打印九九乘法表-课后程序(JavaScript前端开发案例教程-黑马程序员编著-第2章-课后作业)
【案例2-9】打印九九乘法表 一、案例描述 考核知识点 for双重循环 练习目标 掌握for循环应用。实现九九乘法表。 需求分析 九九乘法表相信大家一点也不陌生,之前见到的乘法表是印刷在课程本之上的。而在本案例中我们将用JavaScript代码来实现九九乘法表。 案例分…...
【Linux】基于阻塞队列的生产者消费者模型
🌠 作者:阿亮joy. 🎆专栏:《学会Linux》 🎇 座右铭:每个优秀的人都有一段沉默的时光,那段时光是付出了很多努力却得不到结果的日子,我们把它叫做扎根 目录👉为何要使用…...
)
【华为OD机试 2023最新 】 真正的密码(C++)
文章目录 题目描述输入描述输出描述用例题目解析C++题目描述 在一行中输入一个字符串数组,如果其中一个字符串的所有以索引0开头的子串在数组中都有,那么这个字符串就是潜在密码, 在所有潜在密码中最长的是真正的密码,如果有多个长度相同的真正的密码,那么取字典序最大的…...
)
差分算法(蓝桥杯复习+例题讲解+模板c++)
文章目录差分介绍差分应用区间加区间求和总结3729. 改变数组元素100. 增减序列文章首发于:My Blog 欢迎大佬们前来逛逛 差分介绍 差分是一种常见的算法,用于快速修改数组中某一段区间的值。 差分的思想就是预处理出数组的差分数组,然后修改…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...