NOI2003 逃学的小孩 题解
NOI2003 逃学的小孩 题解
传送门。
题目简述
给定一棵树 T T T,需要选择三个点 A , B , C A,B,C A,B,C,需要从 C C C 走到 A , B A,B A,B 的最远距离。
(第一段题目是在讲剧情吗。。)
前置知识
- 图
- 树
- 树的直径
思路简述
这题在蓝题(提高+ / 省选-)中还是比较水的 ^_^
来看看样例吧
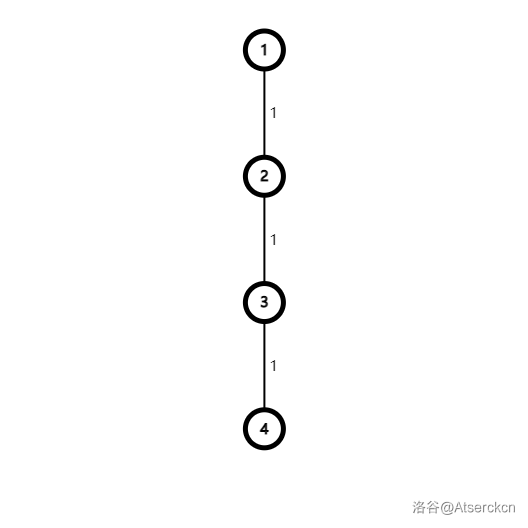
用瞪眼法(——数学老师) 看看,发现 A , B A,B A,B 可以设在 1 1 1 和 4 4 4,然后 C C C 在 2 2 2 或 3 3 3 都无所谓。
那么 4 4 4 是咋来的呢?
(设 C C C 在 2 2 2)
2 → 1 → 4 2\rightarrow 1 \rightarrow4 2→1→4。
由于是最远距离,那么——
树的直径!
而刚好,树的直径就是有两个端点,刚刚好可以一个作为 A A A,一个作为 B B B。
然后 C C C 就是在除了 A , B A,B A,B 的节点,距离 A , B A,B A,B 的最短路径。
那么,直接枚举所有 C C C,取最大值再加上 A → B A\rightarrow B A→B 的距离(直径距离)即可。
代码实现
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=2e5+5;
ll n,m,head[N],cnt_e,u,v,w,top,dis_start[N],dis_stop[N],start,stop,ans,ans2;
struct E{ll from,to,w,pre;
}e[N<<1];
inline void add(ll from,ll to,ll w)//链式前向星
{e[++cnt_e].from=from;e[cnt_e].to=to;e[cnt_e].w=w;e[cnt_e].pre=head[from];head[from]=cnt_e;return;
}
void dfs_d(ll u/*当前节点*/,ll fa/*他爹*/,ll sum/*目前的最长路径*/)//求树的直径
{if(sum>ans)ans=sum,top=u;for(ll i=head[u];i;i=e[i].pre){ll v=e[i].to;if(v==fa) continue;dfs_d(v,u,sum+e[i].w);}return;
}
void dfs_dis_start(int u,int fa)//所有点到某个端点的距离
{for(ll i=head[u];i;i=e[i].pre){ll v=e[i].to;if(v==fa) continue;dis_start[v]=dis_start[u]+e[i].w;dfs_dis_start(v,u);}return;
}
void dfs_dis_stop(int u,int fa)//所有点到另一个端点的距离
{for(ll i=head[u];i;i=e[i].pre){ll v=e[i].to;if(v==fa) continue;dis_stop[v]=dis_stop[u]+e[i].w;dfs_dis_stop(v,u);}return;
}
signed main(){scanf("%lld%lld",&n,&m);for(ll i=1;i<=m;i++){scanf("%lld%lld%lld",&u,&v,&w);add(u,v,w);add(v,u,w);}dfs_d(1,0,0);start=top;ans=0;dfs_d(start,0,0);stop=top;dfs_dis_start(start,0);dfs_dis_stop(stop,0);for(ll i=1;i<=n;i++)//枚举所有可能的Cans2=max(ans2,min(dis_start[i],dis_stop[i]));printf("%lld\n",ans+ans2);//ans:直径距离//ans2:某个点到两个端点的最短距离return 0;
}
小彩蛋
我:不对劲,有问题:
1 ≤ T i ≤ 1 0 9 1\le T_i \le 10^9 1≤Ti≤109
十亿分钟。。。先不说你能不能活到那时候,就算能考试貌似就已经结束了吧。。
相关文章:

NOI2003 逃学的小孩 题解
NOI2003 逃学的小孩 题解 传送门。 题目简述 给定一棵树 T T T,需要选择三个点 A , B , C A,B,C A,B,C,需要从 C C C 走到 A , B A,B A,B 的最远距离。 (第一段题目是在讲剧情吗。。) 前置知识 图树树的直径 思路简…...

硬件服务器操作系统的选择:Linux 还是 Windows?
在这个科技日新月异的时代,云服务器虽然日益普及,但硬件服务器依然是众多云服务和数据中心不可或缺的基石。有趣的是,随着云服务器的兴起,不少工程师竟然未曾亲眼见过实体的硬件服务器。然而,事实是,无论是…...
dataV组件使用——数据更新更新组件
bug 当数据更新只更新一个属性页面不会刷新(this.config1.data arr;) 必须重新赋值整个config 方式一:检测到数据更新重新赋值config this.config1 {data: arr,header: ["所在单位", "人员姓名", "职位", &q…...

solana合约编写
文章目录 solana 合约编写整体思路Cargo.toml配置代码实现在 Solana 智能合约中,定义和管理可能的错误类型自定义一个 Solana 账户结构一个帐户的约束条件什么是bump账号获取指令参数编码基础常用总结format! 格式化字符串Option<String>Vec<u8>编译部署到localne…...

C++调用C#方法(附踩坑点)
C调用C#方法 写在前面效果思路步骤可能的问题 写在后面 写在前面 工作需要用C调用C#写到代码,看来网上写的方法,自己也踩了一些坑,这里总结一下,我只试了CLR的方法。 主要参考了下面几篇博客 C调用C#库简单例程(Lucky…...

开源前端埋点监控插件Web-Tracing
Web-Tracing是一款专为前端项目设计的前端监控插件,它基于JavaScript设计,兼容跨平台使用,并提供了全方位的监控功能。 开源地址:https://gitee.com/junluoyu/web-tracing-analysis 以下是关于Web-Tracing的详细介绍:…...
智慧排水远程监测系统物联网解决方案
智慧排水监测系统是一种集成了现代信息技术、物联网技术、大数据分析及云计算能力的高效城市排水管理解决方案。该系统通过全面、实时地监控城市排水网络的运行状态,旨在预防内涝灾害,优化水资源管理,保障城市安全运行,促进可持续…...
是一个版本控制系统】)
【SVN(Subversion)是一个版本控制系统】
Question SVN所有命令 Answer SVN(Subversion)是一个版本控制系统,用于管理和跟踪文件和目录的更改。以下是一些常用的SVN命令: 检出(Checkout) svn checkout URL从版本库中检出一个工作副本。 更新&am…...

leetcode108.把升序数组转换成二叉搜索树
题目描述 [-10,-3,0,5,9] 转换成如下二叉搜索树: 解题的核心原理是:二叉搜索树的中序遍历结果是一个升序数组,所以根节点的数值,也位于数组的中部。 class Solution {public TreeNode sortedArrayToBST(int[] nums) {return h…...

用QTdesigner制作自己的双目标定软件
目录 1,设计布局软件界面 2,导出界面ui文件为python的.py文件 3,为界面添加对应的功能 4,导出为exe可执行文件 5,运行测试效果 5.1 双击启动 5.2 添加必要的参数 5.3 ,运行结果 效果展示 动手制作双…...

MySQL:基础巩固-DDL
一、对数据库的操作 1.查询所有数据库 SHOW DATABASES;2. 查询当前使用的数据库 SELECT DATABASE();3. 创建数据库 CREATE DATABASE IF NOT EXISTS test DEFAULT CHARSET utf8mb4 COLLATE utf8mb4_general_ci;4. 删除数据库 DROP DATABASE IF EXISTS test;5. 使用数据库 …...

翻译软件在医学中的应用
翻译软件在医学中的应用非常广泛,主要体现在以下几个方面: 患者沟通:翻译软件可以帮助医务人员与非母语患者进行有效沟通,确保患者能够准确表达自己的症状和需求,也使医生能够清晰地解释治疗方案和用药说明。这对提升…...

政务大数据解决方案(六)
政务大数据解决方案通过建立综合数据平台,将来自各政府部门的异构数据整合并进行深入分析,利用人工智能和机器学习技术实现智能化数据处理与预测,从而提升政府决策的科学性和实时响应能力。方案涵盖数据采集、存储、处理、分析与可视化&#…...

【MATLAB机器人系统工具箱】【manipulatorRRT规划器】属性和方法解析
启用了连接启发式(heuristic)后,双向快速扩展随机树(RRT)算法会在以下情况下忽略 MAXCONNECTIONDISTANCE 的限制:当两棵树(起始树和目标树)之间的节点距离足够接近时,算法…...
)
MySQL 多表连接(JOIN)
在数据库开发中,多表连接(JOIN)是一个非常重要的技术,它使得我们可以在查询中整合多个表的数据,进而实现更加复杂的数据操作。本文将深入探讨 MySQL 中的多表连接,帮助读者全面理解 JOIN 的基本概念、类型和…...

Opencv学习-直方图比较
由于图像的直方图表示图像像素灰度值的统计特性,因此可以通过两幅图像的直方图特性比较 两幅图像的相似程度。从一定程度上来讲,虽然两幅图像的直方图分布相似不代表两幅图像相似,但是两幅图像相似则两幅图像的直方图分布一定相似。例如&…...

一文入门:正则表达式基础
正则表达式简介 正则表达式(Regular Expression,简称regex或RE)是一种用于匹配字符串中字符组合的模式。它广泛应用于编程语言、文本编辑器和各种工具中,用于执行复杂的字符串搜索和替换任务。 为什么使用正则表达式?…...

深入理解 `@DateTimeFormat` 和 `@JsonFormat` 注解
前言 在Java应用程序中,处理日期和时间是一个常见的需求。无论是从数据库读取还是通过API接收数据,正确的日期和时间格式都是确保应用正确运作的关键因素。本文将深入探讨两个常用的注解——DateTimeFormat和JsonFormat——以及它们如何帮助我们在Sprin…...

微服务架构设计中的常见的10种设计模式
微服务架构设计的概念 微服务架构(Microservices Architecture)是一种用于构建分布式系统的软件设计模式。它将大型应用程序拆分成一组小型、自治的服务,每个服务都运行在其独立的进程中,服务之间通过轻量级的通信机制(…...

stripe Element 如何使用
这里要准备好几个东西: 一个支付成功过后的回调 还有一个下单的接口 一旦进入这个下单界面,就要去调下单的接口的,用 post, 这个 接口你自己写,可以写在后端中,也可以放到 nextjs 的 api 中。 首先说的是这个下单…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...
