今日（2024 年 8 月 19 日）科技新闻
- 科大讯飞推出星火极速超拟人交互：8 月 19 日，科大讯飞宣布星火语音大模型更新，正式推出星火极速超拟人交互，并将其能力落地在讯飞星火 APP “小星畅聊” 功能中。该交互响应速度更快，能感知用户情绪变化并共情回应，还支持语音可控表达和角色扮演等功能。其在响应和打断速度、情绪感知情感共鸣、语音可控表达、人设扮演四个方面实现突破，让整体交互体验更自然、有趣。这代表国产大模型开始从追赶、对标到自主创新、走出差异化路线。8 月底星火极速超拟人交互将率先全民开放使用。
- 我国陆上超深井钻探速度创造新纪录：据央视网 8 月 19 日消息，我国陆上超深井钻探速度取得新突破，单日进尺达到 2006 米。
- 高能同步辐射光源储存环流强达到新高度：8 月 18 日，国家重大科技基础设施 —— 高能同步辐射光源（HEPS）储存环流强达到 12 毫安，标志着 HEPS 加速器进入调束快行道。HEPS 是我国及亚洲首台第四代同步辐射光源，建成后将可发射比太阳亮度高 1 万亿倍的光，是帮助探测微观世界的利器，可用于实验室研究及解决工业生产中的实际问题。经过 5 年建设，HEPS 储存环于今年 7 月 23 日正式开机调束，预计年内发射第一束光并投入应用。
- 微软的研究人员提出智能体框架 AgentInstruct，仅需使用原始数据源，就能自动创建大量、多样化的合成数据。经过合成数据微调后的模型 Orca-3，在多项基准上刷新了 SOTA，其在数学方面的表现性能暴涨 168%。该框架可解决大模型训练中高质量数据缺乏的问题。
- 我国成功发射千帆极轨 01 组卫星；
- 低真空环境下试验取得成功，“高速飞车” 正驶来；
- 人工合成淀粉技术取得新突破；
- 我国西北地区海拔最高风电场首批机组投运；
- 全国最大电力北斗精准位置服务网建成；
- 新型材料可大量捕捉水中有毒金属离子；
相关文章：
今日（2024 年 8 月 19 日）科技新闻
科大讯飞推出星火极速超拟人交互：8 月 19 日，科大讯飞宣布星火语音大模型更新，正式推出星火极速超拟人交互，并将其能力落地在讯飞星火 APP “小星畅聊” 功能中。该交互响应速度更快，能感知用户情绪变化并共情回应&…...
Python 虚拟环境
为什么要创建虚拟环境 创建 Python 虚拟环境的主要目的是为了解决依赖管理的问题，特别是在开发多个项目或部署应用程序时，虚拟环境具有以下几个优势： 依赖隔离： 不同的项目可能需要不同版本的 Python 解释器和库。通过创建虚拟环…...
Redis RDB三两事
rdb：将数据库的快照以二进制格式保存在文件中，redis重启后直接加载数据。可以通过save和bgsave命令生成rdb。当然我们可以在生成rdb文件时指定规则，例如 save 60 1000 如果60秒内不少于1000个key发生了改动，则生成一个新的rdb文件…...
分布式高可用架构设计
一、限流 1、单机限流 如图，应用C的资源c/x被上游的应用A和应用C并发访问，应用C的系统能力支持c/x资源最高5000/qps的访问量；为了不让高并发流量或尖峰流量压垮应用C，可以针对应用C的资源c/x做限流；比如设置限流4500…...
GATK SampleList接口介绍
在 GATK 中，SampleList 是一个接口，用于表示一个样本列表。这些样本通常是在基因组分析过程中被处理的不同生物样本。SampleList 接口提供了访问这些样本的一些基本方法，通常用于多样本分析任务，比如变异检测或基因组重测序。 SampleList 接口的方法 SampleList 接口定义…...
00后是真卷不过，工作没两年，跳槽到我们公司起薪20K都快接近我了
在程序员职场上，什么样的人最让人反感呢? 是技术不好的人吗?并不是。技术不好的同事，我们可以帮他。 是技术太强的人吗?也不是。技术很强的同事，可遇不可求，向他学习还来不及呢。 真正让人反感的，是技术平平&…...
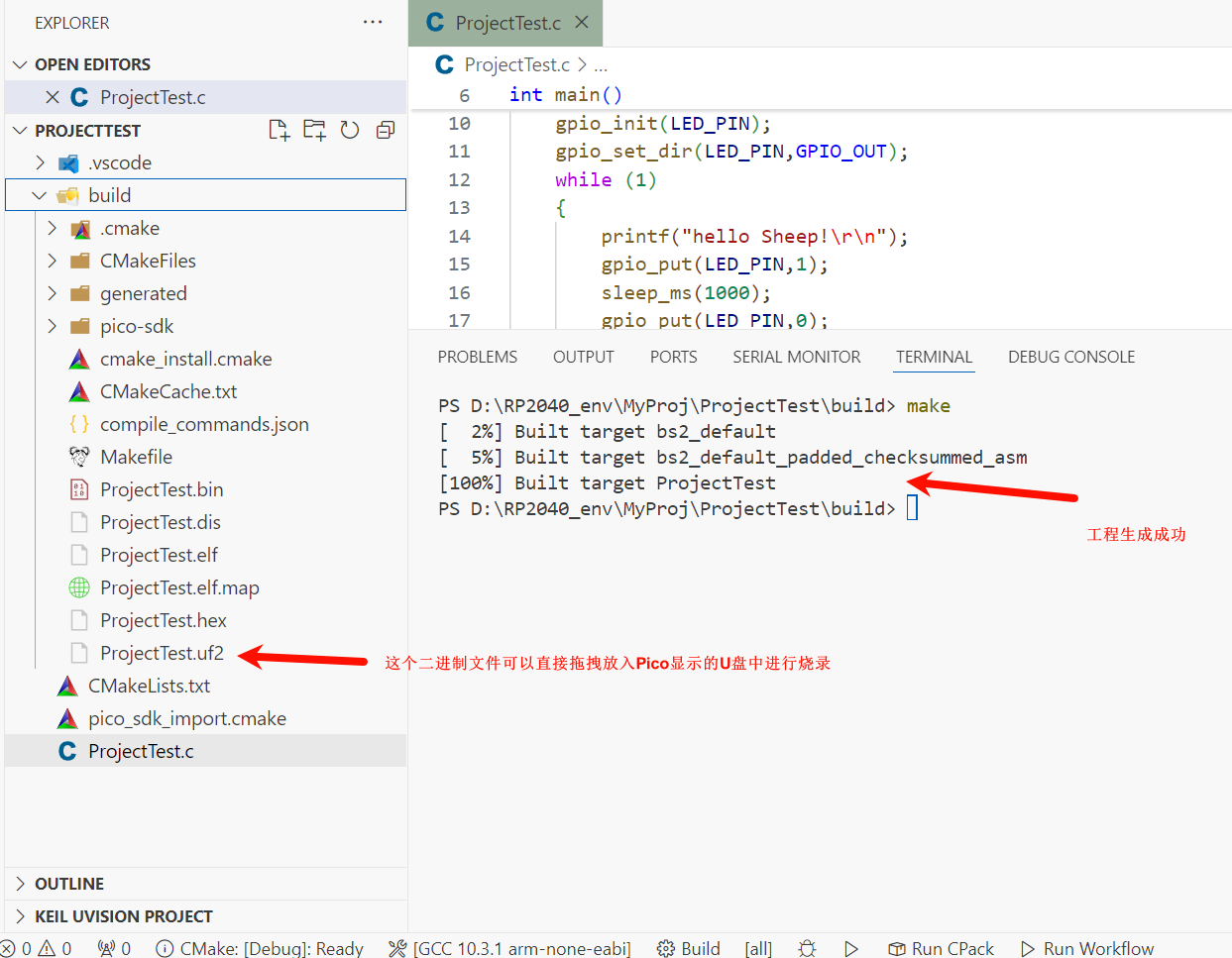
树莓派Pico C/C++ 开发环境搭建(一键完成版)
树莓派Pico C/C 开发环境搭建(一键完成版) 因为之前使用过MicroPython开发过树莓派Pico，总觉得用起来怪怪的。正好最近树莓怕发布了新一代的MCU——RP2350，之前的RP2040在各个平台都有所降价，因此，买了几块。同时因为之前是玩stm…...
【计算机组成原理】二、数据的表示和运算：1.数值与编码（十进制二进制转换、BCD码、ASCII码、汉字编码、奇偶校验码、循环冗余检测CRC、海明码）
二、数据的表示和运算 文章目录 二、数据的表示和运算1.数值与编码1.1数据存储和排列❗1.2十进制转换1.2.1整数1.2.2小数 1.3二进制转换1.3.1 B->O1.3.2 B->H 1.4真值&机器数1.5 BCD码1.6 ASCII码1.7汉字与GBK1.8 UTF1.9检错码1.9.1奇偶校验码1.9.2循环冗余检测CRC1.…...
汇编语言中的艺术：数据压缩与解压缩技术
标题：汇编语言中的艺术：数据压缩与解压缩技术 数据压缩是计算机科学中的一项基本技术，它通过减少数据的冗余来降低存储或传输所需的空间。在低级语言如汇编语言中实现数据压缩和解压缩，不仅是一种技术挑战，也是对硬件…...
【Alibaba Cola 状态机】重点解析以及实践案例
【Alibaba Cola 状态机】重点解析以及实践案例 1. 状态模式 状态模式是一种行为型设计模式，允许对象在内部状态改变时改变其行为，简单地讲就是，一个拥有状态的context对象，在不同状态下，其行为会发生改变。看起来是改…...
购买商城源码前需要考虑哪些方面？
前言 购买商城源码前需要考虑的方面包括功能满足、技术兼容性、可扩展性、公司实力、客户评价、安全性与稳定性等。 购买商城源码是一项重要决策，需要综合考虑多个因素。以下是详细的考虑方面： 1.功能满足： 确保所选的源码能够支持企业所…...
MongoDB快速入门CRUD
1. 数据库管理 1.1 切换数据库 切换到名为 myDatabase 的数据库。如果该数据库不存在，MongoDB 会在第一次写入数据时自动创建它。 use myDatabase;1.2 查看当前数据库 显示当前使用的数据库的名称。 db; 1.3 显示所有数据库 列出当前 MongoDB 实例中的所有数…...
【python基础】—利用pandas读取或写入mysql表数据
文章目录 一、read_sql()二、to_sql()三、连接数据库方式—MySQL1、用sqlalchemy包构建数据库链接2、用DBAPI构建数据库链接 四、容易遇到的问题 一、read_sql() 功能 将 SQL 查询/数据库表读入 DataFrame。 语法 读取数据库（通过SQL语句或表名） pand…...
C/C++信号量
文章目录 一、信号量介绍1.1 什么是信号量1.2 信号量的原子性1.3 信号量的使用 二、C语言使用2.1 函数接口2.2 信号量代码 三、C20使用3.1 函数接口 四、C11模拟信号量 一、信号量介绍 1.1 什么是信号量 信号量是一种特殊的变量，是操作系统层面的，可以…...
SSL Pining 问题解决方案
实战案例 为了能够更好的复现 SSL Pining 场景，我们对一个 App（https:app4.scrape.center）进行抓包，这个 App 包含了 SSL Pining 的相关设置，如果我们将手机的代理设置为抓包软件提供的代理服务，那么这个 …...
【Spring Boot】全局异常处理
目录 背景 前言 设计步骤 1.定义异常信息类： 2.自定义异常： 3.创建全局异常处理类 4.在控制器中抛出异常 5.输出 捕获 Valid 校验异常 背景 去面试的时候被问到SpringBoot项目中，如何处理全局异常的，也就是如何捕获全局异…...
安全基础学习-SM3加密算法
SM3是一种广泛使用在中国国家标准中的哈希算法，全称为“中国国家密码算法SM3”。它由中国国家密码管理局制定，主要用于数字签名和消息完整性验证。SM3算法与SHA-256在结构上类似，但其设计具有特定的改进以增强安全性。 SM3算法生成256位的哈希值，使用了32轮的迭代运算，并…...
MySQL中处理JSON数据：大数据分析的新方向
1. 简介 1.1. 概述 在MySQL中处理JSON数据的能力是在MySQL 5.7版本中引入的，并在后续的版本中不断得到增强。这使得MySQL能够直接操作和查询JSON格式的数据，极大地扩展了其处理复杂数据结构的能力。 1.2. 主要特点 灵活性与可扩展性 ：JSON允许开发者存储不规则和嵌套的数…...
K8S 容器调度
在Kubernetes中，容器调度是一个自动化的过程，负责将容器（在Kubernetes中称为Pod）分配到集群中的合适节点上运行。这一过程由Kubernetes的调度器（kube-scheduler）控制，它通过一系列算法和策略来确…...
C++ //练习 17.2 定义一个tuple，保存一个string、一个vector＜string＞和一个pair＜string, int＞。
C Primer（第5版） 练习 17.2 练习 17.2 定义一个tuple，保存一个string、一个vector和一个pair<string, int>。 环境：Linux Ubuntu（云服务器） 工具：vim 代码块 /**********************…...
web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段： 构建阶段（Build Stage）：…...
TDengine 快速体验（Docker 镜像方式）
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能，本节首先介绍如何通过 Docker 快速体验 TDengine，然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker，请使用 安装包的方式快…...
华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...
[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法，且在 O(n) 时间复杂度…...
HarmonyOS运动开发：如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit（传感器服务）# 前言 在运动类应用中，运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据，如配速、距离、卡路里消耗等，用户可以更清晰…...
纯 Java 项目（非 SpringBoot）集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目（非 SpringBoot）集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
Go语言多线程问题
打印零与奇偶数（leetcode 1116） 方法1：使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型（算法、数据分析、机器学习等）不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...
在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率：以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码：冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...
机器学习的数学基础：线性模型
线性模型 线性模型的基本形式为： f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法，得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...