力扣 | 背包dp | 279. 完全平方数、518. 零钱兑换 II、474. 一和零、377. 组合总和 Ⅳ
文章目录
- 一、279. 完全平方数
- 二、518. 零钱兑换 II
- 三、474. 一和零
- 四、377. 组合总和 Ⅳ
一、279. 完全平方数
LeetCode:279. 完全平方数

朴素想法:
这个题目最简单的想法是,可以用 O ( n n ) O(n\sqrt{}n) O(nn)的动态规划解决,定义dp[i]表示整数i完全平方数的最少数量。
由于我们不太能知道都有哪些可以构成,我们直接枚举 k k k,且满足 k 2 < = i k^2<=i k2<=i,找出最小的即可。
class Solution {
public:int numSquares(int n) {vector<int> dp(n + 1, 0x3f3f3f3f);dp[0] = 0;for(int i = 1; i <= n; ++ i){for(int k = 1; k <= sqrt(i); ++ k){dp[i] = min(dp[i], dp[i - k * k] + 1);}}return dp[n];}
};
问题抽象:
这个问题是否也能转化成 完全背包问题?
相当于 1 1 1~ n n n可以无限选择,达到背包容量n,并且使得放入的数最少。
我们可以定义 d p [ i ] [ j ] dp[i][j] dp[i][j] 表示达到j,能够选择 1 1 1~ i i i,所使用的最小数字,那么我们就可以像完全背包一样进行状态转移了。(注意这里i最大是 n \sqrt{}n n,因此时间复杂度也是 n n n\sqrt{n} nn)
我们仔细看一下 可以发现,实际上和方法一就是循环调个位置。
class Solution {
public:int numSquares(int n) {vector<int> dp(n + 1, 0x3f3f3f3f);dp[0] = 0;for(int k = 1; k <= sqrt(n); ++ k){for(int i = k * k; i <= n; ++ i){dp[i] = min(dp[i], dp[i - k * k] + 1);}}return dp[n];}
};
那么,我们如何抽象问题为完全背包问题? 到目前为止,我们还不能直接进行问题抽象,而是看到题有类似的样子才做出完全背包的想法。
我们来看看,之前考虑过的问题,整数拆分、322. 零钱兑换、518. 零钱兑换 II 。
他们都是 有无限个"物品"可以选择、这些物品组合成"背包"里的物品(无论是体积还是质量)、最后需要达成一个目标
这个目标就是我们定义的状态、
这个物品就是我们要规定什么时候能包含的、
这个背包就是总的容量
比如这个完全平方数,我们要定义的状态是和为i的最少完全平方数的数量,我们要规定的物品是 1 1 1~ n \sqrt{n} n,我们的最后容量就是n。
不过我们需要注意的是,放入背包的物品没有顺序要求。
二、518. 零钱兑换 II
LeetCode:518. 零钱兑换 II

普通的完全背包问题,做到这里已经不需要优化了,直接写了,因为写的完全背包太多了。
完全背包问题更新:
不过完全背包要注意的是,从小往大来遍历,因为可以选择无限个,
dp[j - coins[i]]这个转移,表示的是容量为j的这个背包一部分用来装一个coins[i],其余部分就是dp[j - coins[i]]的部分,这个部分是可以包含coins[i]的。 我们来思考一下这个转移对不对?我们来把背包具象化,dp[j - coins[i]]个容量为j - coins[i]的不同背包,它们都是互不相同的,且都可能包含coins[i]因为coins[i]没有个数限制。然后我们把这些不同的背包都加上coins[i]这个物品,这几个背包不同的! 不信你拿出来看看,一个一个比!这一部分是至少包含一个coins[i]的可能性。而之前的dp[j]是不包含任何coins[i]的可能性。
class Solution {
public:int change(int amount, vector<int>& coins) {vector<int> dp(amount + 1, 0);dp[0] = 1;for(int i = 0; i < coins.size(); ++ i){for(int j = coins[i]; j <= amount; ++ j){dp[j] = dp[j] + dp[j - coins[i]];}}return dp[amount];}
};
三、474. 一和零
LeetCode:474. 一和零

这是一个0-1背包问题,也就是,这里每个元素只能选择一次。
这里可以定义两维来表示0和1的个数,dp[i][j]表示最多有i个0和j个1的最长子集长度。
那么我们来考虑当前考虑字符串时,我们提取出它的0的个数和1的个数,假如分别为k和p,那么就可以进行一次转移。
dp[u][i][j] = max(dp[u - 1][i -k][j - p], dp[u - 1][i][j]
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<vector<int>>> dp(strs.size() + 1, vector<vector<int>>(m + 1, vector<int>(n + 1, 0)));for(int i = 1; i <= strs.size(); ++ i){int zero_num = Get(strs[i - 1]);int one_num = (int) strs[i - 1].size() - zero_num;for(int j = 0; j <= m; ++ j){for(int k = 0; k <= n; ++ k){dp[i][j][k] = dp[i - 1][j][k];if(j >= zero_num && k >= one_num)dp[i][j][k] = max(dp[i][j][k], dp[i - 1][j - zero_num][k - one_num] + 1);}}}return dp[strs.size()][m][n];}
private:int Get(string & s){int ans = 0;for(auto ch : s){if(ch == '0') ++ ans;}return ans;}
};
空间优化:
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> dp(m + 1, vector<int>(n + 1));for(int i = 1; i <= strs.size(); ++ i){int zero_num = Get(strs[i - 1]);int one_num = (int) strs[i - 1].size() - zero_num;for(int j = m; j >= zero_num; -- j){for(int k = n; k >= one_num; -- k){dp[j][k] = max(dp[j][k], dp[j - zero_num][k - one_num] + 1);}}}return dp[m][n];}
private:int Get(string & s){int ans = 0;for(auto ch : s){if(ch == '0') ++ ans;}return ans;}
};
我们来看看空间优化先后的状态转移的区别,实际上空间优化后,它直接继承了所有的前面的部分。
空间优化前很容易出错:
容易写成这样:
for(int j = zero_num; j <= m; ++ j){for(int k = one_num; k <= n; ++ k){dp[i][j][k] = max(dp[i - 1][j][k], dp[i - 1][j - zero_num][k - one_num] + 1);}
}
仔细思考发现转移方程确实没错,dp[i][j][k]表示考虑前i个字符串,0的个数最多为j,1的个数最多为k,我们单独拿出来strs[i - 1],其余部分是dp[i - 1][j - zero_num][k -one_num]这一部分也是对的定义,那么转移也是对的。那么问题出在哪呢?
问题出在,当 j < z e r o _ n u m j < zero\_num j<zero_num和 k < o n e _ n u m k < one\_num k<one_num时,我们没有进行状态转移,换句话说,没有考虑当当前背包容量不能容纳strs[[i - 1]时,可以放strs[0] ~ strs[i - 2],也就是说必须直接继承,因为考虑前i个字符串确实有东西可以放的话 你不继承就错了。
四、377. 组合总和 Ⅳ
LeetCode:377. 组合总和 Ⅳ

这里和零钱兑换II的区别在于,这里的元素是有顺序的。 零钱兑换II没有顺序,就像背包内放物品是没有顺序的。那么我们仅仅使用背包的思想肯定是不能得到答案的,毕竟这里有放入顺序。
既然有顺序,那我们枚举每一个容量的最后一个物品就能保证这几个的放法都不一样了,因此可以这样进行状态转移。
也就是说,我们从最小容量开始枚举它最后一个物品,来保证它放的内容不一样,然后依次枚举容量,你会发现我们保证了每个容量的最后一个都不一样,这确实能做到有顺序的问题。(排列问题,毕竟小容量也考虑了这些物品,这些物品可以无限次放。)
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<long long> dp(target + 1);dp[0] = 1;int mod = INT_MAX;for(int i = 1; i <= target; ++ i){for(int j = 0; j < nums.size(); ++ j){if(i >= nums[j])dp[i] = (dp[i] + dp[i - nums[j]]) % mod;;}}return dp[target];}
};
题目中有一个坑的,就是说答案在int范围内,但是中间结果可能爆int,这里有两个解决方案:
(1)使用long long然后取模,long long是为了保证中间结果的计算爆int,取模是将结果映射到int范围内,对于答案来说必然是没有错误的,因为答案本身就在int范围内,映射过后还是本身。
(2)对于爆int的进行摒弃,原因在于,答案不可能用它来转移,这种背包不可能转移到其他人身上,不然会产生链锁反应,即使是转移了,那些人也必然对答案没有贡献,不然就爆int了。
for (int i = 1; i <= target; i++) {for (int& num : nums) {if (num <= i && dp[i - num] < INT_MAX - dp[i]) {dp[i] += dp[i - num];}}}
相关文章:

力扣 | 背包dp | 279. 完全平方数、518. 零钱兑换 II、474. 一和零、377. 组合总和 Ⅳ
文章目录 一、279. 完全平方数二、518. 零钱兑换 II三、474. 一和零四、377. 组合总和 Ⅳ 一、279. 完全平方数 LeetCode:279. 完全平方数 朴素想法: 这个题目最简单的想法是,可以用 O ( n n ) O(n\sqrt{}n) O(n n)的动态规划解决&#x…...

【ECMAScript性能优化的技巧与陷阱】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...

Swift实时监听判断是否连接有网络WIFI和蜂窝数据
本章节讲解如何使用swift连接网络,实时的监听到网络的状态,在主界面中进行调用,网络包含Wi-Fi 和 蜂窝。 1.封装一个判断是否有网络的类 2.在封装类注册通知 3.主界面接收注册通知,并且调用封装的网络类 4.成功测试,有…...
Flink Source 数据源)
(三)Flink Source 数据源
Flink 数据源主要分为内置数据源和第三方数据源。其中内置数据源包含文件、Socket 连接、集合类型数据等,不需要引入其它依赖库。第三方数据源定义了 Flink 和外部系统数据交互的逻辑,Flink 提供了非常丰富的数据源连接器,例如 Kafka、Elasticsearch、RabbitMQ、JDBC 等。 …...

第四届机电一体化、自动化与智能控制国际学术会议(MAIC 2024)
目录 大会官网 会议简介 组织机构 大会主席 程序委员会主席 主讲嘉宾 征稿主题 参会说明 大会官网 http://www.icmaic.org 会议简介 第四届机电一体化、自动化与智能控制国际学术会议(MAIC 2024)将于2024年9月27-29日在中国成都召开。MAIC 20…...
leetcode 089 打家劫舍
leetcode 089 打家劫舍 题目 一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响小偷偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。 给定…...
)
等保测评基础知识(六)
《计算机病毒防治管理办法》51号令 第十四条 从事计算机设备或者媒体生产、销售、出租、维修行业的单位和个人,应当对计算机设备或者媒体进行计算机病毒检测、清除工作,并备有检测、清除的记录。 第十九条 计算机信息系统的使用单位有下列行为之一的,由公安机关处以警告…...
作业帮 TiDB 7.5.x 使用经验
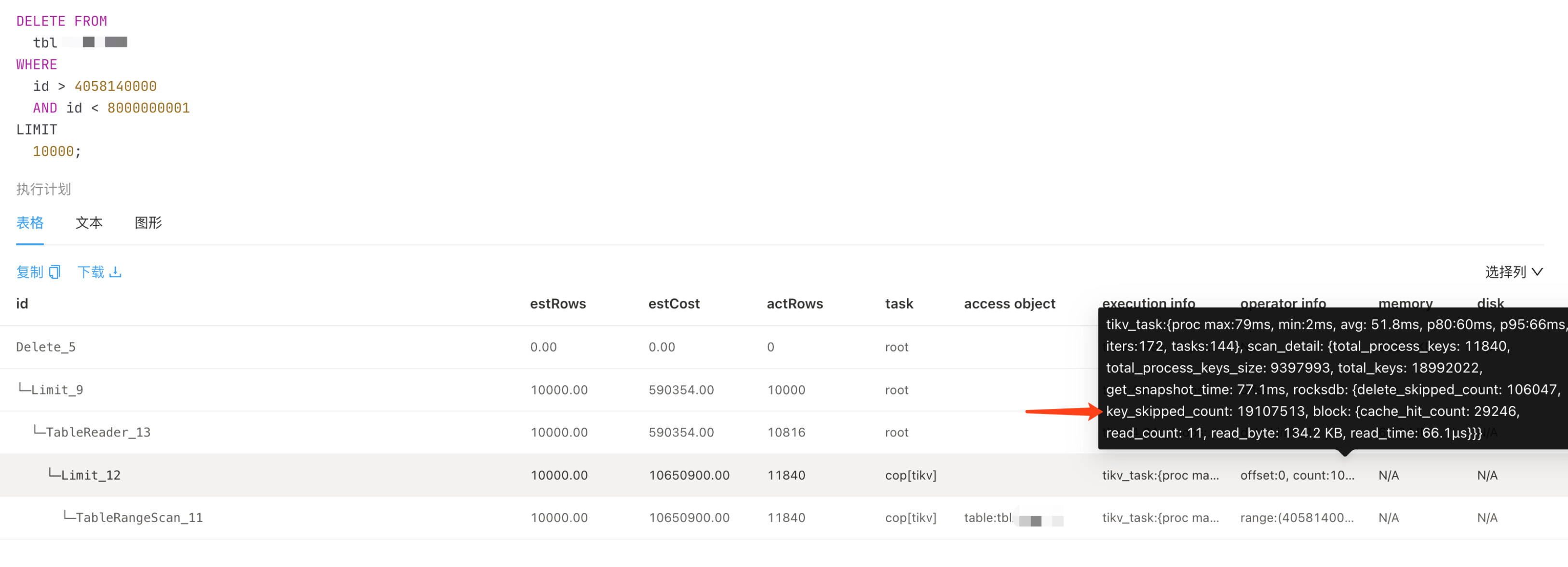
作者: 是我的海 原文来源: https://tidb.net/blog/5f9784d3 近期在使用 TiDB 时遇到的一些小问题的梳理总结,大部分版本都在6.5.6和7.5.2 1、limit 导致的扫描量过大的优化 研发定时任务每天需要扫描大量数据,到时机器网卡被…...

c语言练习题1
1.输出Helloword /*输出Helloword*/ #include<stdio.h> int main() {printf("Hello word!");return 0; }2.整型变量的定义与使用 /*整型变量的定义与使用*/ #include <stdio.h> int main() {int a;int b;a 10;b 20;int c a b;int d a - b;printf(…...

嵌入式开发就业方向有哪些?前景未来可期!
在科技日新月异的今天,嵌入式系统几乎渗透到了我们生活的各个角落。从简单的家用电器到复杂的工业自动化设备,再到我们手中的智能手机,无一不体现出嵌入式技术的魅力。因此,嵌入式领域的就业前景广阔,为众多求职者提供…...

系列:水果甜度个人手持设备检测-github等开源库和方案
系列:水果甜度个人手持设备检测 -- github等开源库和方案 概述 通常来说,年纪轻轻的我们一般都喜欢走捷径,对于智能设备和算法软件领域来说,GitHub应该算为数不多的的捷径之一。就算因为效果不好/知识产权/方向不同等原因不用,…...

Visual Studio中 生成版本号
Visual Stuodio WPF项目 自动生成版本号 生成递增版本号 软件版本号主要标识了软件的版本,通过其可以了解软件、类库文件的当前版本,使得软件版本控制有所依据。 我们也可以在项目属性上可以看到相关设置的界面,对应的英文名称分别为&#…...

AI入门指南(四):分类问题、回归问题、监督、半监督、无监督学习是什么?
文章目录 一、前言二、分类问题、回归问题是什么?分类问题概念常见算法分类问题的实际应用:银行贷款审批案例 回归问题概念常见算法回归问题实际应用:线性回归模型预测房价 小结 三、监督、半监督、非监督学习是什么?监督学习非监…...

Linux下本地端口转发
在Linux下进行本地端口转发处理,可以进行如下操作: 1.确认NetFilter相关驱动编译到内核,并且CONFIG_IP_NF_TARGET_REDIRECTy; 2.开启转发功能:echo 1 > /proc/sys/net/ipv4/ip_forward; 3.设置转发规…...
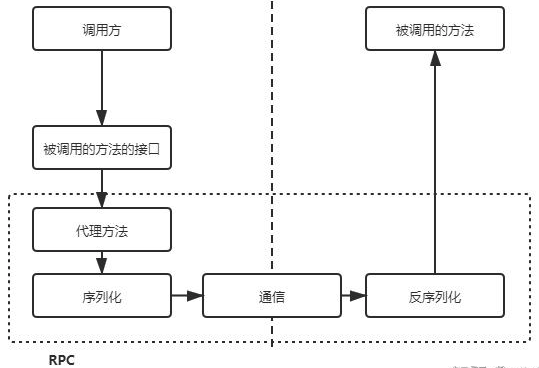
RPC 和 HTTP 理解
网上充斥着各类类似于这样的文章:rpc 比 http 快了多少倍?既然有了 http,为什么还要用 rpc 调用等等。遇到这类文章,说明对 http 和 rpc 是由理解误区的。 这里再次重复强调一遍,通信协议不是 rpc 最重要的部分&#x…...

Visual Studio 2022 v17.11 发布
Visual Studio 2022 版本 17.11 正式发布 (GA),此版本主要是基于用户反馈的各项改进。 “每项增强、每项修复和每项新功能均根据你的反馈而制定。无论你是在构建 Web、桌面、云还是游戏应用程序,Visual Studio 2022 v17.11 都旨在让你的开发体验更流畅、…...

通讯专题-RS232
1 概述 RS-232是一种点对点通信协议,这意味着每个数据信号沿一根导线传输(差分信号使用两根导线传输一个数据信号),RS-232为全双工方式运行(总线可同时发送和接收数据)。 根据新修订的标准为容性负载为2500…...

桥接模式详解
桥接模式 概念: 将抽象部分和实现部分分离, 使他们都可以独立的变化 概念很抽象, 难以理解, 我们举个例子 例子 设想三种不同品牌的汽车 大车 中车 小车 三种不同类型的引擎 纯电引擎 混动引擎 燃油引擎 如果我们把他们两两组合, 都继承同一个类的话,就会有9个类, 并且如果后…...

使用一致性哈希解决哈希分片负载均衡的扩展性问题
声明:本文的图全部源于:小林coding 上来咱先说,一致性哈希是应对分布式系统的算法 假设有一个负载均衡问题,也就是大批流量来请求,那怎么分配这些流量? 随机?还是挨个轮询? 这都…...

探索 Resolume Arena 7 - 引领 VJ 音视频创作的卓越软件
Resolume Arena 7 是一款专为 Mac 和 Windows 系统设计的强大 VJ 音视频软件,为创意专业人士和爱好者提供了丰富而出色的功能。 这款软件拥有直观且用户友好的界面,即使对于初学者来说,也能快速上手并开始创作。其强大的媒体管理功能&#x…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...
