卡特兰数、斯特林数基础
卡特兰数
从格点(0,0)(0,0)(0,0)走到格点(n,n)(n,n)(n,n),只能向右或向上走,不能穿过对角线,的路径的条数,称为卡特兰数HnH_nHn。
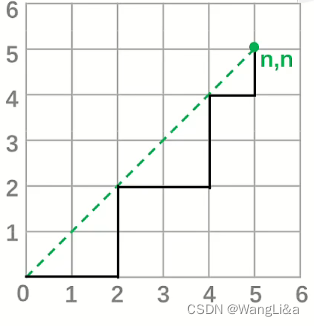
则有H0=1H_0=1H0=1。
通项公式:
- Hn=(2nn)−(2nn−1)H_n=\begin{pmatrix} 2n\\ n \end{pmatrix}-\begin{pmatrix} 2n\\ n-1 \end{pmatrix}Hn=(2nn)−(2nn−1)
- Hn=(2nn)n+1H_n=\frac {\begin{pmatrix} 2n\\ n \end{pmatrix}}{n+1}Hn=n+1(2nn)
- Hn=4n−2n+1Hn−1H_n=\frac{4n-2}{n+1}H_{n-1}Hn=n+14n−2Hn−1
折线法
证明一下卡特兰数的公式。
先证明公式1:
如果没有限制,那么路径总数是,从2n2n2n步移动之中,选出nnn步向上走,另外nnn步向右走的方案数(2nn)\begin{pmatrix} 2n\\ n \end{pmatrix}(2nn)。
如果有限制,我们画出y=x+1y=x+1y=x+1的函数图像,碰到这条线,意味着不合法。
把所有不合法的路径沿着这条图像对折过来,其终点必然是(n−1,n+1)(n-1,n+1)(n−1,n+1)。
换句话说,所有到达(n−1,n+1)(n-1,n+1)(n−1,n+1)的路径,都对应着到达(n,n)(n,n)(n,n)的一条不合法路径。因此答案就是(2nn)−(n+1+n−1n−1)\begin{pmatrix} 2n\\ n \end{pmatrix}-\begin{pmatrix} n+1+n-1\\ n-1 \end{pmatrix}(2nn)−(n+1+n−1n−1)
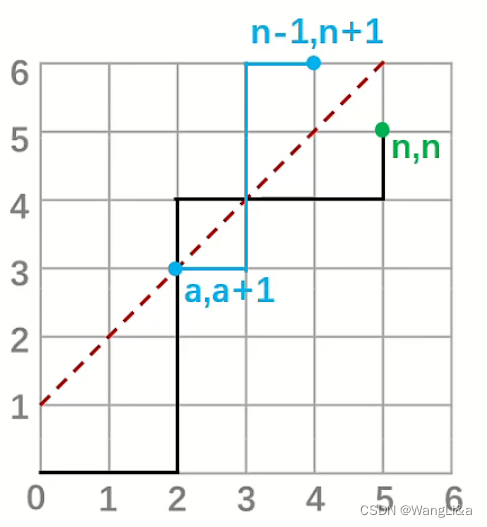
QED.
证明一下公式2:
(2nn)−(2nn−1)\begin{pmatrix} 2n\\ n \end{pmatrix}-\begin{pmatrix} 2n\\ n-1 \end{pmatrix}(2nn)−(2nn−1)
=(2n)!n!n!−(2n)!(n+1)!(n−1)!=\frac{(2n)!}{n!n!}-\frac {(2n)!}{(n+1)!(n-1)!}=n!n!(2n)!−(n+1)!(n−1)!(2n)!
=(2n)!n!(n−1)!n−(2n)!n!(n−1)!(n+1)=\frac{(2n)!}{n!(n-1)!n}-\frac {(2n)!}{n!(n-1)!(n+1)}=n!(n−1)!n(2n)!−n!(n−1)!(n+1)(2n)!
=(2n)!n!(n−1)!⋅(1n−1n+1)=\frac{(2n)!}{n!(n-1)!}\cdot\left(\frac{1}{n}-\frac 1{n+1}\right)=n!(n−1)!(2n)!⋅(n1−n+11)
=(2n)!n!(n−1)!n−(2n)!n!(n−1)!(n+1)=\frac{(2n)!}{n!(n-1)!n}-\frac {(2n)!}{n!(n-1)!(n+1)}=n!(n−1)!n(2n)!−n!(n−1)!(n+1)(2n)!
=(2n)!n!(n−1)!⋅(1n−1n+1)=\frac{(2n)!}{n!(n-1)!}\cdot\left(\frac{1}{n}-\frac 1{n+1}\right)=n!(n−1)!(2n)!⋅(n1−n+11)
=(2n)!n!(n−1)!⋅1n(n+1)=\frac{(2n)!}{n!(n-1)!}\cdot\frac {1}{n(n+1)}=n!(n−1)!(2n)!⋅n(n+1)1
=(2n)!n!n!⋅1n+1=\frac{(2n)!}{n!n!}\cdot\frac {1}{n+1}=n!n!(2n)!⋅n+11
=(2nn)⋅1n+1=\begin{pmatrix} 2n\\ n \end{pmatrix}\cdot\frac {1}{n+1}=(2nn)⋅n+11
QED.
证明一下公式3:
留作习题,读者自证不难。
常见情况
特点:一种操作不能超过另一种操作,或操作之间不能有交集。
例如:
- 一个由nnn个000,nnn个111组成的长度为2n2n2n的字符串,满足所有前缀中,111的个数不能超过000的个数,这样的子串数量。
- 包含nnn组括号的合法表达式的数量。
(想要括号序列合法,必须保证所有前缀中,左括号的数量大于等于右括号的数量) - 一个栈的进栈序列为1,2,...,n1,2,...,n1,2,...,n,则出栈序列的可能数量。
(必须保证出栈数量小于等于进栈数量) - 在圆上选择2n2n2n个点,连接起来形成nnn条不相交的弦的方案数。
(把nnn条不相交的弦映射为括号序列,把弦的左端映射为左括号,右端映射为右括号) - 通过连接顶点将n+2n+2n+2条边的正多边形分为nnn个三角形的方案数(三角剖分)。
(想要保证分为nnn个三角形,必须保证连接的线不相交) - nnn个节点可以构造多少颗不同的二叉树?
考虑对n+2n+2n+2条边的多边形三角剖分,把剖分得出的三角形抽象为一个节点,对它相邻的三角形连边,最后得出必定是一颗二叉树。 - 一段连乘积有多少种运算次序?
(相当于给连乘积加括号)
公式法
事实上有:
Hn=∑i=0n−1HiHn−i−1H_n=\overset{n-1}{\underset{i=0}\sum}H_iH_{n-i-1}Hn=i=0∑n−1HiHn−i−1
可以从两个方面来证明一下:
- 出栈序列
考虑iii是最后一个出栈的数,则[1,i−1][1,i-1][1,i−1]在iii进栈之前就出栈了,情况数有Hi−1H_{i-1}Hi−1种,而iii后面的n−in-in−i个数,则必然在iii出栈前就出栈了,情况数有Hn−iH_{n-i}Hn−i种,枚举这个iii,得到
Hn=∑i=1nHi−1Hn−i=∑i=0n−1HiHn−i−1H_n=\overset{n}{\underset{i=1}\sum}H_{i-1}H_{n-i}=\overset{n-1}{\underset{i=0}\sum}H_iH_{n-i-1}Hn=i=1∑nHi−1Hn−i=i=0∑n−1HiHn−i−1 - 格点计数
我们知道,在格点卡特兰数的要求中,路径不能越过对角线。我们可知,在走到终点之前的一步,一定是向上走的:

红色表示最后一步。
显然,碰到对角线之后,一定是向右走的,我们枚举对角线上的一个点,使得走完向右走的那一步之后,不能越过新的对角线,统计的路径条数:

绿色,枚举的位置。
红色,最后一步。
蓝色,新的对角线。
此时我们发现,从底下走到绿色圆圈,不能越过对角线。与从绿色箭头走到红色圆圈,不能越过蓝线,是两个更小的卡特兰数问题,因此可以用乘法原理计数。
我们注意到,我们枚举的一种新的情况,在我们枚举的更旧的情况中都属于不合法情况,不会被重复统计。
QED.
用公式同样可以解释各种卡特兰数的情况。
- 一个由nnn个000,nnn个111组成的长度为2n2n2n的字符串,满足所有前缀中,111的个数不能超过000的个数,这样的子串数量。
注意到最后一个字符一定是111,枚举一个位置的000,使得这个000与末尾的那个111匹配,转化为格点计数的情况。 - 包含nnn组括号的合法表达式的数量。
同理。 - 一个栈的进栈序列为1,2,...,n1,2,...,n1,2,...,n,则出栈序列的可能数量。
同理。 - 在圆上选择2n2n2n个点,连接起来形成nnn条不相交的弦的方案数。
同理,枚举一个点与最后那个点(任意指定一个固定的点为最后的点)连接成弦。 - 通过连接顶点将n+2n+2n+2条边的正多边形分为nnn个三角形的方案数(三角剖分)。
同理4。 - nnn个节点可以构造多少颗不同的二叉树?
枚举根节点有iii个左子树,则就会有n−i−1n-i-1n−i−1个右子树,显然。
斯特林数
第一类斯特林数
定义[nm]\begin{bmatrix}n\\ m\end{bmatrix}[nm]表示nnn元集合划分为mmm个非空环排列的方案数,即无符号第一类斯特林数,或简称为第一类斯特林数,斯特林轮换数。
第一类斯特林数有递推式:
[nm]=[n−1m−1]+(n−1)[n−1m]\begin{bmatrix} n\\ m \end{bmatrix}=\begin{bmatrix} n-1\\ m-1 \end{bmatrix}+(n-1)\begin{bmatrix} n-1\\ m \end{bmatrix}[nm]=[n−1m−1]+(n−1)[n−1m]
递推式容易证明,留作习题。
第二类斯特林数
定义{nm}\begin{Bmatrix} n\\ m \end{Bmatrix}{nm}表示将nnn元集合划分为mmm个非空子集的方案数,即第二类斯特林数,或斯特林子集数。
第二类斯特林数有递推式:
{nm}={n−1m−1}+m{n−1m}\begin{Bmatrix} n\\ m \end{Bmatrix}=\begin{Bmatrix} n-1\\ m-1 \end{Bmatrix}+m\begin{Bmatrix} n-1\\ m \end{Bmatrix}{nm}={n−1m−1}+m{n−1m}
递推式容易证明,留作习题。
其他
- 两类斯特林数的边界条件都是s[0][0]=1s[0][0]=1s[0][0]=1。
- 从递推式可以看出,斯特林数增长比组合数还要快。
- 斯特林数用于解决组合计数问题,以及用于斯特林反演。这些问题较复杂,单独讨论。
后记
于是皆大欢喜。
相关文章:

卡特兰数、斯特林数基础
卡特兰数 从格点(0,0)(0,0)(0,0)走到格点(n,n)(n,n)(n,n),只能向右或向上走,不能穿过对角线,的路径的条数,称为卡特兰数HnH_nHn。 则有H01H_01H01。 通项公式: Hn(2nn)−(2nn−1)H_n\begin{pmatrix} 2n\\ n \en…...
STL——mapmultimap和setmultiset
一、关联式容器 与序列式容器相同,关联式容器也是用于存储数据的,不同的是,关联式容器里存储的是<key, value>结构的键值对,在数据检索时比序列式容器效率更高。 二、键值对 用来表示具有一一对应的一种结构,该…...
2023热门抖音权重查询小程序源码
2023热门抖音权重查询小程序源码 跟抖音上很火的一模一样,小程序适配优化。接口免费。小程序不是网页 修改教程: 1,如果想修改或者去除水印,直接删除或修改“index.html”12~22行 2,如果想修改logo,直接…...

153.网络安全渗透测试—[Cobalt Strike系列]—[生成hta/exe/宏后门]
我认为,无论是学习安全还是从事安全的人多多少少都会有些许的情怀和使命感!!! 文章目录一、后门简介1、hta后门2、exe后门3、宏病毒后门二、生成后门并测试0、测试环境1、生成hta后门并测试2、生成exe后门并测试3、生成宏病毒后门…...

如何成为优秀的程序员
崔宝秋,现任小米首席架构师、小米云平台负责人。1995年赴美留学,纽约州立大学石溪分校计算机科学系博士毕业,曾任IBM高级工程师和高级研发经理、雅虎搜索技术核心团队主任工程师、LinkedIn主任工程师,2012年回国加入小米科技。 20…...
多线程(四):线程安全
在开始讲解线程安全之前我们先来回顾一下我们学了那些东西了: 1. 线程和进程的认识 2. Thread 类的基本用法 3. 简单认识线程状态 4. 初见线程安全 上一章结束时看了一眼线程安全问题,本章将针对这个重点讲解。 一个代码在单线程中能够安全执行&am…...
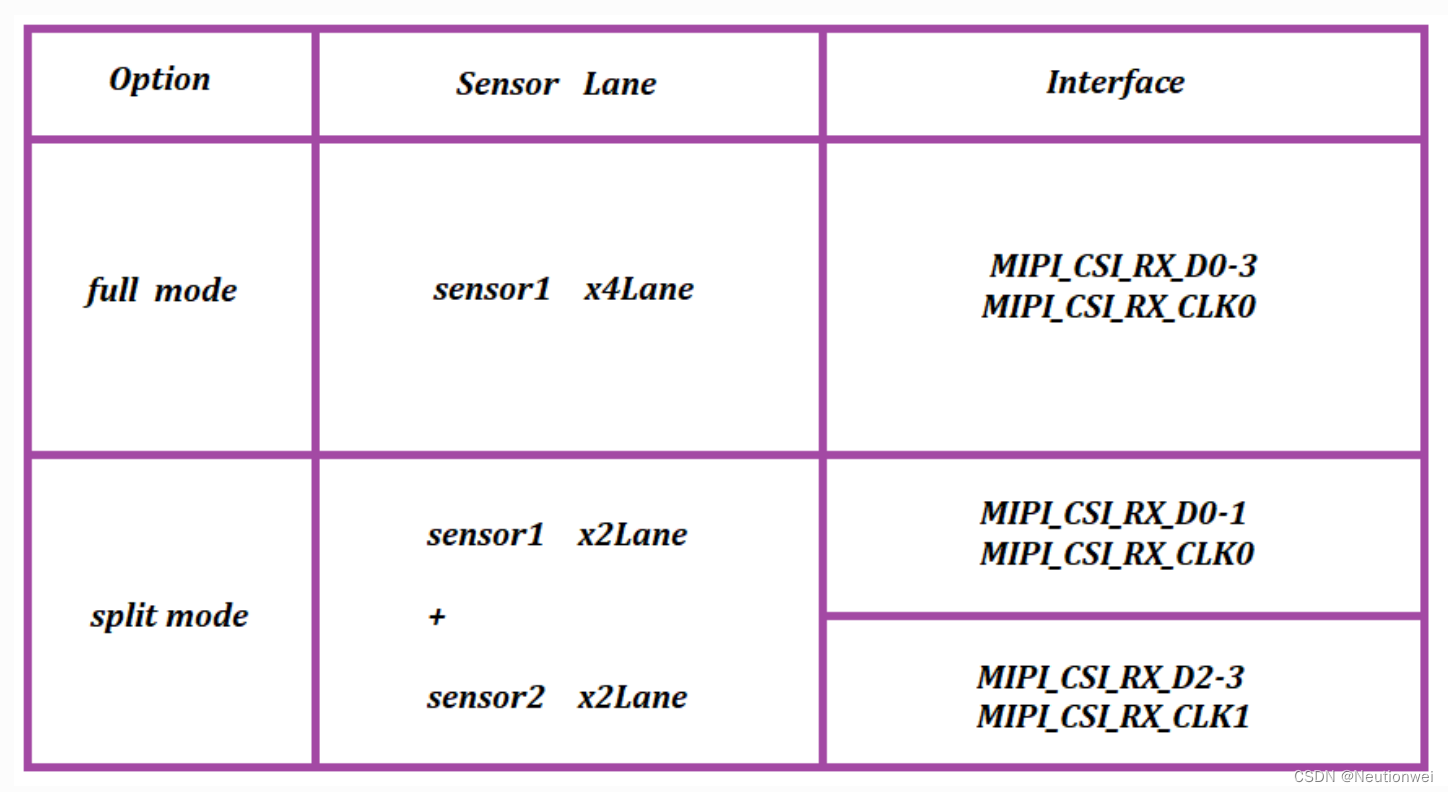
[ROC-RK3568-PC] [Firefly-Android] 10min带你了解Camera的使用
🍇 博主主页: 【Systemcall小酒屋】🍇 博主追寻:热衷于用简单的案例讲述复杂的技术,“假传万卷书,真传一案例”,这是林群院士说过的一句话,另外“成就是最好的老师”,技术…...

C++之模拟实现string
文章目录前言一、包含的相关头文件二、构造和析构1.构造函数2.拷贝构造1.传统写法2.现代写法3.赋值运算符重载1.传统写法2.现代写法4.析构函数三、iterator四、modify1.push_back(尾插一个字符)2.append(尾插一个字符串)3.运算符重载1.尾插字…...
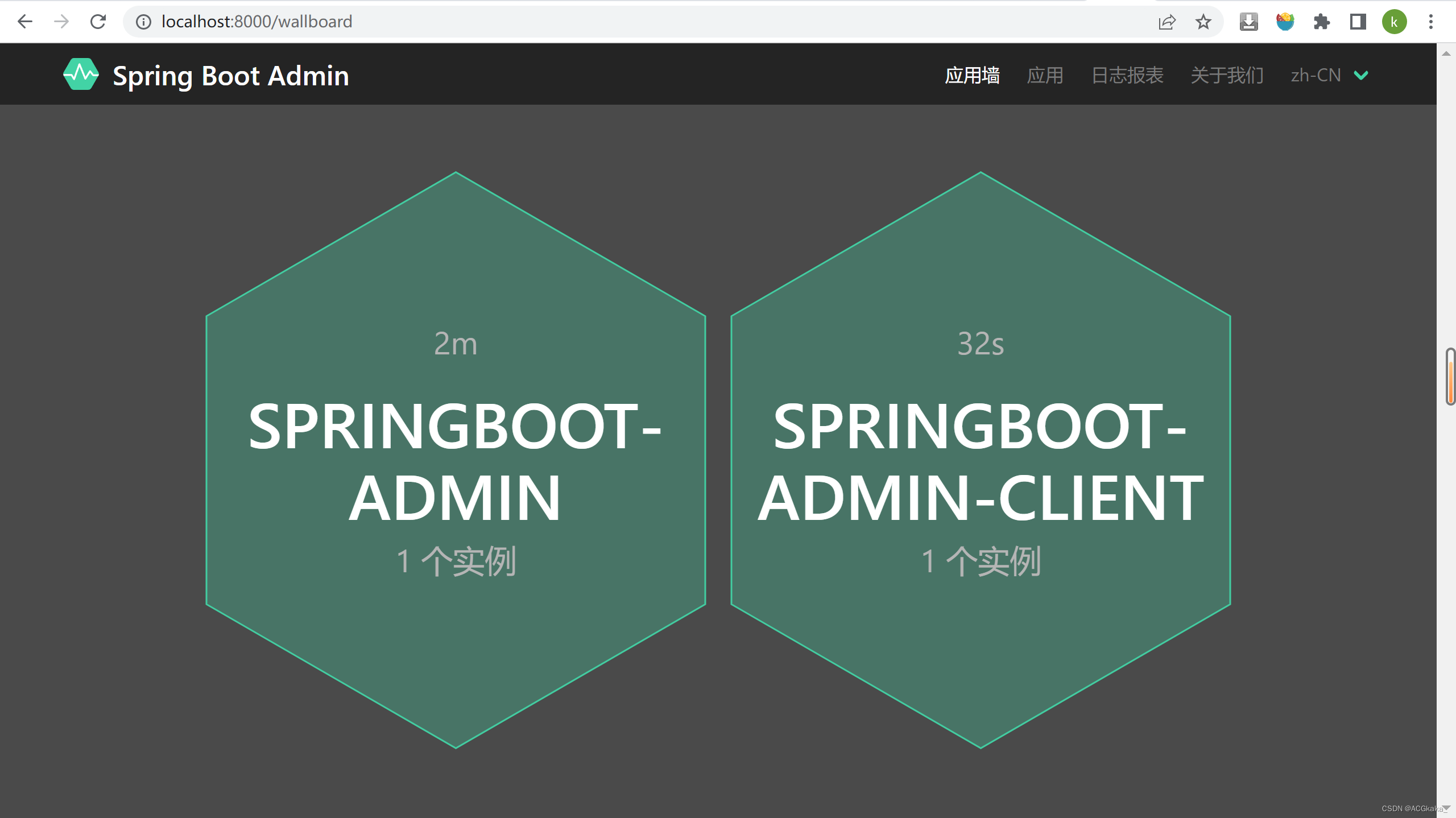
SpringBoot实战(十三)集成 Admin
目录一、简介二、搭建 springboot-admin 管理服务1.Maven 依赖2.application.yml3.添加 EnableAdminServer4.启动服务,查看页面三、搭建 springboot-admin-client 客户端服务1.Maven 依赖2.application.yml3.启动服务,查看页面四、搭配 Eureka 使用1.搭建…...

mke2fs命令:建立ext2文件系统
以下内容源于网络资源的学习与整理,如有侵权请告知删除。 使用格式 mke2fs [options] [设备名称] [区块数] options与含义 -c:检查是否有损坏的区块。-F:不管指定的设备为何,强制执行mke2fs。-M:记录最后一次挂入的…...

免费分享一个springboot+vue的办公系统
springbootvue的OA系统项目介绍项目部署项目特点项目展示项目介绍 这是一个采用前后端分离开发的项目,前端采用 Vue 开发、后端采用 SpringBoot Mybatis 开发。 很适合java初学者练手和学习。 前端技术:Vue3.2 Vue-Router Pinia Ant Design Vue 3.X…...
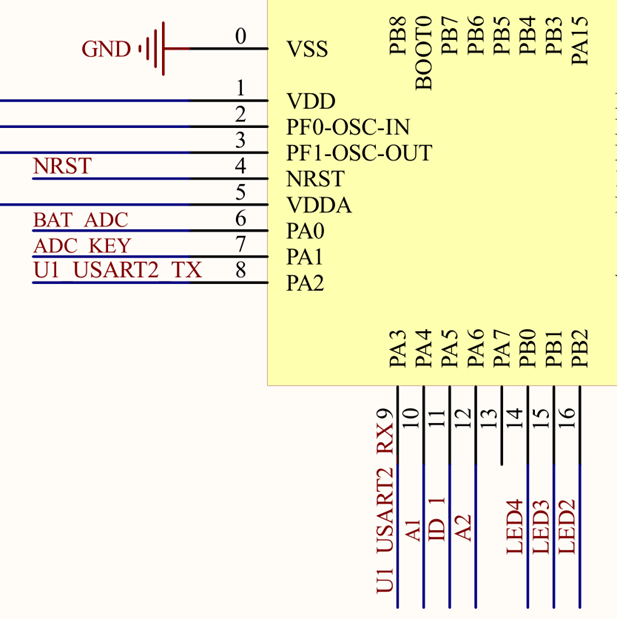
STM32数据搬运工DMA
DMA的概念DMA,全称为:Direct Memory Access,即直接存储器访问。DMA 传输方式无需 CPU 直接控制传输,也没有中断处理方式那样保留现场和恢复现场的过程,通过硬件为 RAM 与 I/O 设备开辟一条直接传送数据的通路ÿ…...

4、操作系统——进程间通信(2)(system V-IPC介绍)
目录 一、system V-IPC常识 1、key和ID 2、文件描述符 3、函数(ftok) ftok产生IPC对象的健值key(类似文件路径) 4、例子 5、使用命令查看或删除当前系统中的IPC对象 一、system V-IPC常识 1、key和ID (1&#x…...

基于CentOS Stream 9平台搭建Nacos2.0.4集群以及OpenResty反向代理
目录展示Nacos2.0.4集群搭建1. 下载2. 解压3.修改配置3.1分别修改下启动类中JDK路径以及启动大小3.2 分别配置数据源3.3 创建nacos数据库3.4 修改cluster.conf配置3.4.1 复制并修改3.4.2 编辑文件,修改三台主机地址3.4.3 分别放入另外两个nacos的conf目录下:4. 启动…...

老杜MySQL入门基础 第二天
导入演示数据 1、连接MySQL 2、创建"bjpowernode"数据库 create database bjpowernode;3、选择数据库 use bjpowernode4、导入数据 source D:\bjpowernode.sql(文件的路径)1 去除重复记录(把查询结果去除重复记录)(原表数据不会改变) 使用关键字dist…...
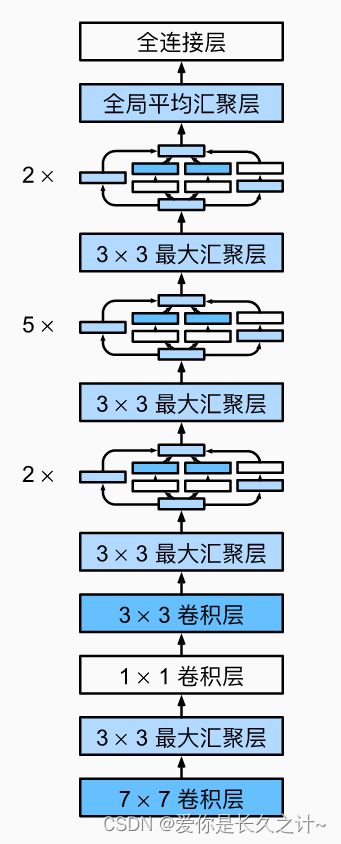
Python深度学习实战:人脸关键点(15点)检测pytorch实现
引言 人脸关键点检测即对人类面部若干个点位置进行检测,可以通过这些点的变化来实现许多功能,该技术可以应用到很多领域,例如捕捉人脸的关键点,然后驱动动画人物做相同的面部表情;识别人脸的面部表情,让机…...

linux简单入门
目录Linux简介Linux目录结构Linux文件命令文件处理命令文件查看命令常用文件查看命令Linux的用户和组介绍Linux权限管理Linux简介 Linux,全称GNU/Linux,是一种免费使用和自由传播的类UNIX操作系统,其内核由林纳斯本纳第克特托瓦兹࿰…...
给准备面试网络工程师岗位的应届生一些建议
你听完这个故事,应该会有所收获。最近有一个23届毕业的大学生和我聊天,他现在网络工程专业大四,因为今年6、7月份的时候毕业,所以现在面临找工作的问题。不管是现在找一份实习工作,还是毕业后找一份正式工作࿰…...
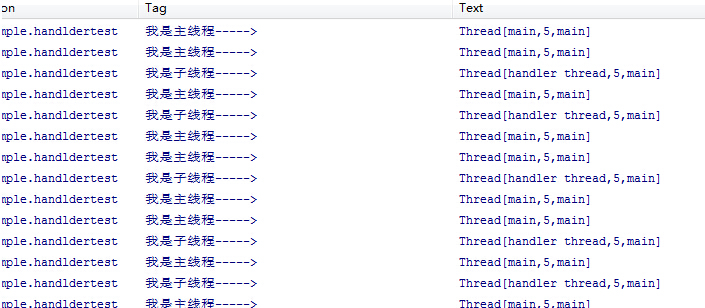
主线程与子线程之间相互通信(HandlerThread)
平时,我们一般都是在子线程中向主线程发送消息(要在主线程更新UI),从而完成请求的处理。那么如果需要主线程来向子线程发送消息,希望子线程来完成什么任务。该怎么做?这就是这篇文章将要讨论的内容。 一、…...

13基于双层优化的电动汽车日前-实时两阶段市场竞标
MATLAB代码:基于双层优化的电动汽车日前-实时两阶段市场竞标 关键词:日前-实时市场竞标 电动汽车 双层优化 编程语言:MATLAB平台 参考文献:考虑电动汽车可调度潜力的充电站两阶段市场投标策略_詹祥澎 内容简介:…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
