密码学之RSA算法
文章目录
- 1. RSA算法介绍
- 1.2 算法历史与发展
- 1.3 算法应用场景
- 2. RSA密钥生成
- 2.1 选择素数
- 2.2 计算公钥和私钥
- 2.3 密钥长度与安全性
- 3 算法原理
- 3.1 加密原理
- 3.2 加密方法
- 3.3 加密示例
- 3.4 代码实现
- 4. 总结
1. RSA算法介绍
1.2 算法历史与发展
RSA算法由Ron Rivest、Adi Shamir和Leonard Adleman于1977年提出,得名于他们姓氏的首字母。最初设计用于解决密钥分发问题,现已广泛应用于数据加密、数字签名等。
1.3 算法应用场景
RSA算法广泛应用于:
- 网络安全:如HTTPS、SSL/TLS协议。
- 数字签名:确保数据完整性和真实性。
- 身份认证:网银、VPN等。
- 电子邮件加密:保障邮件内容安全。
2. RSA密钥生成
2.1 选择素数
在RSA算法中,密钥生成的第一步是选择两个大素数,通常表示为(p)和(q)。这两个素数需要足够大,以确保安全性。素数的选择是随机的,且在实际应用中,它们的位数通常在1024位到2048位之间。
选择素数的过程可以用以下伪代码表示:
def select_primes(length):while True:p = random_prime(length)q = random_prime(length)if p != q:return p, q
在上述伪代码中,random_prime函数用于生成一个指定长度的随机素数。
2.2 计算公钥和私钥
选定 p p p和 q q q后,接下来的步骤是计算公钥和私钥。
- 计算模数 n n n:模数 n n n是 p p p和 q q q的乘积,即 n = p × q n = p \times q n=p×q。这个值将用于加密和解密过程中的模运算。
- 计算欧拉函数 ϕ ( n ) \phi(n) ϕ(n): ϕ ( n ) \phi(n) ϕ(n)表示小于或等于 n n n的正整数中与 n n n互质的数的个数,计算公式为$phi(n) = (p-1) \times (q-1)$。
- 选择公钥指数 e e e: e e e必须满足 1 < e < ϕ ( n ) 1 < e < \phi(n) 1<e<ϕ(n),并且 e e e和 ϕ ( n ) \phi(n) ϕ(n)互质。常用的 e e e值包括3和65537。
- 计算私钥指数 d d d: d d d是 e e e模 ϕ ( n ) \phi(n) ϕ(n)的乘法逆元,即满足 e × d ≡ 1 ( m o d ϕ ( n ) ) ) e \times d \equiv 1 \pmod{\phi(n)}) e×d≡1(modϕ(n)))。
公钥和私钥的计算可以用以下伪代码表示:
def calculate_keys(p, q, e):n = p * qphi_n = (p - 1) * (q - 1)d = modular_inverse(e, phi_n)return (e, n), (d, n)
2.3 密钥长度与安全性
密钥长度是RSA算法安全性的关键因素。密钥越长,破解的难度越大。目前,一个2048位的RSA密钥被认为是安全的。然而,随着计算能力的提升,密钥长度可能会进一步增加。
密钥长度与安全性的关系可以用以下公式表示:
安全性 ≈ 密钥长度 log 2 ( 3 ) \text{安全性} \approx \text{密钥长度}^{\log_2(3)} 安全性≈密钥长度log2(3)
- 选择两个大素数 p, q] --> B[计算 n = p * q
- 计算 φ(n) = (p-1)(q-1)
- 选择 e,满足 1 < e < φ(n) 且 gcd(e, φ(n)) = 1
- 计算 d,满足 e * d ≡ 1 (mod φ(n))
- 公钥 (n, e) 私钥 (n, d)
3 算法原理
3.1 加密原理
RSA加密算法的核心原理基于大数分解的困难性。其安全性依赖于以下数学原理:
-
欧拉函数:对于任意正整数 n n n,欧拉函数 φ ( n ) \varphi(n) φ(n) 表示小于或等于 n n n 且与 n n n 互质的正整数的个数。如果 n n n 是两个互质数 p p p 和 $q$ 的乘积,那么 φ ( n ) = ( p − 1 ) ( q − 1 ) \varphi(n) = (p-1)(q-1) φ(n)=(p−1)(q−1)。
-
模反元素:对于与 n n n 互质的整数 e e e,存在一个整数 d d d 使得 e d ≡ 1 ( m o d φ ( n ) ) ed \equiv 1 \pmod{\varphi(n)} ed≡1(modφ(n))。 d d d 是 e e e关于模 φ ( n ) \varphi(n) φ(n) 的模反元素。
-
欧拉定理:如果 a a a 和 n n n 互质,那么 a φ ( n ) ≡ 1 ( m o d n ) a^{\varphi(n)} \equiv 1 \pmod{n} aφ(n)≡1(modn)。
根据以上原理,RSA算法的公钥和私钥可以表示为:
- 公钥: ( e , n ) (e, n) (e,n),其中 e e e 是加密密钥, n n n是模数。
- 私钥: ( d , n ) (d, n) (d,n),其中 d d d 是解密密钥。
3.2 加密方法
RSA加密过程可以表示为以下步骤:
-
密钥生成:选择两个大质数 p p p 和 q q q,计算 n = p q n = pq n=pq 和 φ ( n ) = ( p − 1 ) ( q − 1 ) \varphi(n) = (p-1)(q-1) φ(n)=(p−1)(q−1),选择 e e e 使得 1 < e < φ ( n ) 1 < e < \varphi(n) 1<e<φ(n) 且 g c d ( e , φ ( n ) ) = 1 gcd(e, \varphi(n)) = 1 gcd(e,φ(n))=1,计算 d d d 使得 e d ≡ 1 ( m o d φ ( n ) ) ed \equiv 1 \pmod{\varphi(n)} ed≡1(modφ(n))。
-
明文转换:将明文 M M M 转换为整数 m m m,满足 0 ≤ m < n 0 \leq m < n 0≤m<n。
-
加密过程:使用公钥 ( e , n ) (e, n) (e,n) 加密明文 m m m,计算 c ≡ m e ( m o d n ) c \equiv m^e \pmod{n} c≡me(modn),其中 c c c 是密文。
3.3 加密示例
假设我们有以下参数:
- p = 61 p = 61 p=61
- q = 53 q = 53 q=53
- n = p × q = 3233 n = p \times q = 3233 n=p×q=3233
- φ ( n ) = ( p − 1 ) ( q − 1 ) = 3120 \varphi(n) = (p-1)(q-1) = 3120 φ(n)=(p−1)(q−1)=3120
- 选择 e = 17 e = 17 e=17(常用的 e e e 值是 65537)
- 计算 d d d 使得 17 d ≡ 1 ( m o d 3120 ) 17d \equiv 1 \pmod{3120} 17d≡1(mod3120),假设 d = 2753 d = 2753 d=2753
给定明文 M = 65 M = 65 M=65,转换为整数 m = 65 m = 65 m=65,使用公钥 ( e , n ) = ( 17 , 3233 ) (e, n) = (17, 3233) (e,n)=(17,3233) 加密:
c ≡ m e ( m o d n ) c \equiv m^e \pmod{n} c≡me(modn)
c ≡ 6 5 17 ( m o d 3233 ) c \equiv 65^{17} \pmod{3233} c≡6517(mod3233)
c = 2790 c = 2790 c=2790
密文 c c c 为 2790。
3.4 代码实现
以下是使用Python实现RSA加密和解密的示例代码:
import random
from math import gcd# 生成密钥
def generate_keys(p, q):n = p * qphi = (p - 1) * (q - 1)e = random.randrange(2, phi)d = Nonewhile d is None or d >= phi or gcd(d, phi) != 1:k = random.randrange(phi)d = k * e % phiif d == 1:d = k + phireturn ((e, n), (d, n))# 加密函数
def encrypt(m, e, n):return pow(m, e, n)# 解密函数
def decrypt(c, d, n):return pow(c, d, n)# 示例
p = 61
q = 53
(e, n), (d, _) = generate_keys(p, q)
message = 65
encrypted_msg = encrypt(message, e, n)
decrypted_msg = decrypt(encrypted_msg, d, n)print(f"明文: {message}")
print(f"密文: {encrypted_msg}")
print(f"解密后的明文: {decrypted_msg}")
4. 总结
RSA算法以其安全性和广泛的应用在现代密码学中占据重要地位。然而,随着计算能力的提高和量子计算的发展,RSA的安全性可能会受到挑战。未来的加密算法需要在安全性和效率之间找到新的平衡点。
相关文章:

密码学之RSA算法
文章目录 1. RSA算法介绍1.2 算法历史与发展1.3 算法应用场景 2. RSA密钥生成2.1 选择素数2.2 计算公钥和私钥2.3 密钥长度与安全性 3 算法原理3.1 加密原理3.2 加密方法3.3 加密示例3.4 代码实现 4. 总结 1. RSA算法介绍 1.2 算法历史与发展 RSA算法由Ron Rivest、Adi Shami…...

教你学习企业高性能web服务器-nginx
一、web服务介绍 1、Apache的三种模型 (1)Apache prefork 预派生模式,有一个主控制进程,然后生成多个子进程,使用select模型,最大并发1024每个子进程有一个独立的线程响应用户请求相对比较占用内存&…...

封装通用第三方平台用户表(微信开放平台)
文章目录 一. 注册微信开放平台1.1 开发者资质认证1.2 应用申请1.3 配置应用 二.通用数据库表设计三.入库实体类四. 对接第三方平台4.1 微信开放平台VO对象4.2 通用方法 我们的系统可能要对接很多第三方系统,为了便利用户授权使用和对多平台账户的管理。有必要设计通…...

【C++】_string类字符串详细解析(1)
假如没有给你生命,你连失败的机会都没有。你已经得到了最珍贵的,还需要抱怨什么!💓💓💓 目录 ✨说在前面 🍋知识点一:什么是string? •🌰1.string类的概念 •…...

【Linux】——进程概念(万字解读)
一 冯诺依曼体系结构 在此之前,我们先要理解我们计算机的冯诺依曼体系结构,因为是进程的基础 我们所有的操作其实都是基于这样一个模型,比如你在qq上,和别人发送消息,这个消息肯定是先通过输入设备进行输入…...
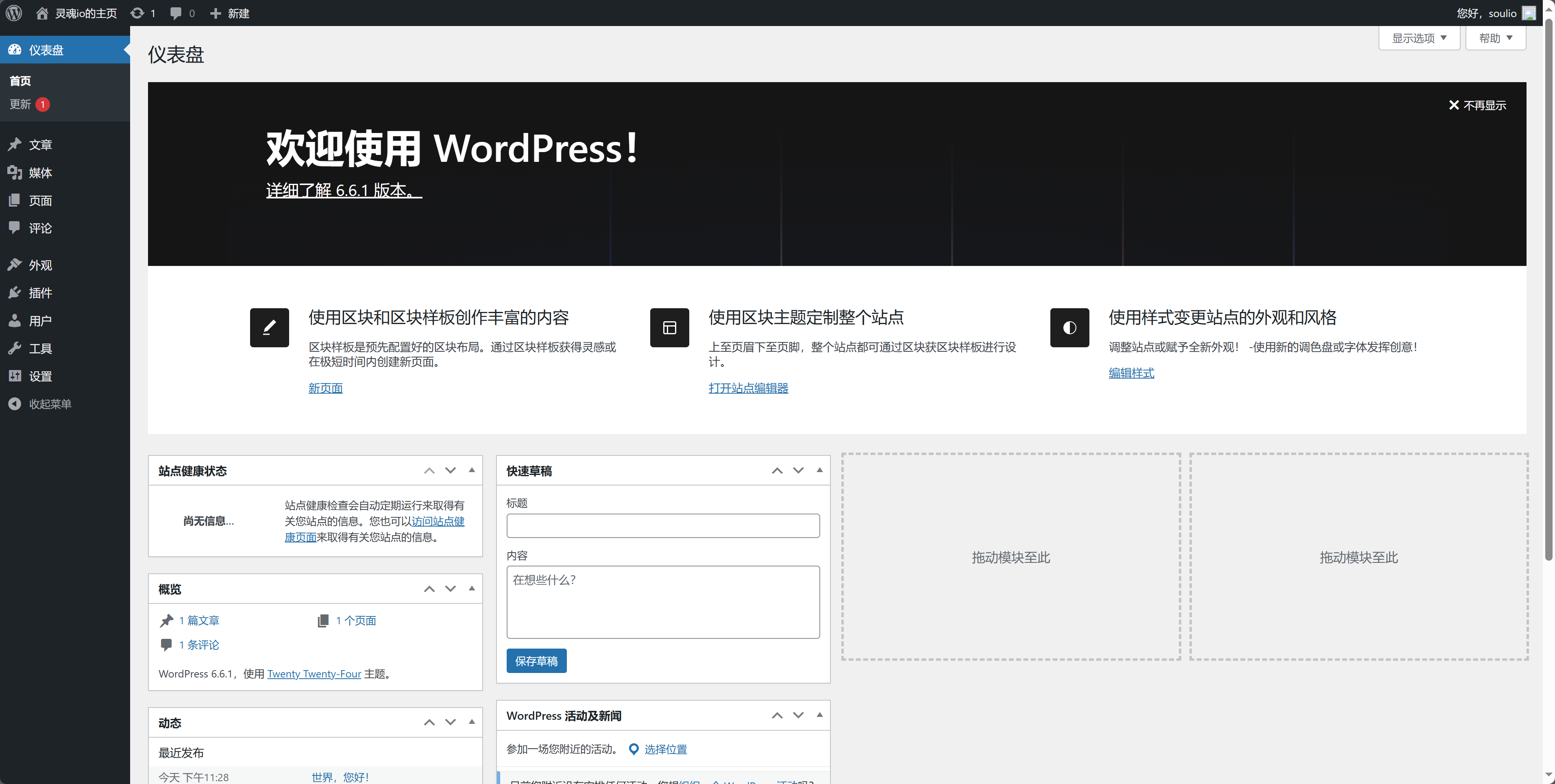
03 serv00搭建WordPress
第一步 下载 serv00 官方教程 按官方教程下载 WordPress 压缩包,解压,将 WordPress 项目文件夹重命名为 public_html(先删除原来的 public_html) 第二步 安装 完成以上步骤后访问你的网站,开始安装 WordPress …...

伪共享问题如何解决?
伪共享问题是多核处理器环境下常见的性能瓶颈之一,特别是在多线程编程中。想要解决它,就必须先了解缓存行的概念。 缓存行 缓存行是指在 CPU 缓存中最小的数据单位,通常包含一定数量的字节(例如,常见的缓存行大小为 …...

基于web框架的协同过滤的美食推荐系统【数据爬虫、管理系统、数据可更新、样式可调整】
文章目录 有需要本项目的代码或文档以及全部资源,或者部署调试可以私信博主项目介绍研究背景研究的目的与意义协同过滤算法基于用户的协同过滤算法定义基于物品的协同过滤算法的定义 数据库设计db_food(美食信息表)db_collect(美食…...

Eureka中的多实例配置:如何处理微服务实例动态扩展与缩减
Eureka中的多实例配置:如何处理微服务实例动态扩展与缩减 1. 引言 在微服务架构中,服务的动态扩展与缩减是确保系统弹性和高可用性的关键因素。Eureka,作为一个服务注册和发现的组件,扮演着至关重要的角色。它由Netflix开源&…...

Ubuntu 22.04使用 IPTables 配置防火墙
网络安全管理是服务器安全的重要组成部分。在这将介绍在 Ubuntu 22.04 中使用名为 iptables 的软件包管理工具设置防火墙的过程。 IPTables简介 IPTables是一个功能强大的软件包管理工具,可用于大多数Linux发行版,包括Ubuntu 22.04。该工具允许管理员定…...

Java语言程序设计——篇十三(1)
🌿🌿🌿跟随博主脚步,从这里开始→博主主页🌿🌿🌿 欢迎大家:这里是我的学习笔记、总结知识的地方,喜欢的话请三连,有问题可以私信🌳🌳&…...

GB/T 5023.3-2008额定电压450/750V及以下聚氯乙烯绝缘电缆
聚氯乙烯绝缘电缆产品分为固定布线用无护套电缆、固定布线用护套电缆、轻型无护套软电缆、一般用途护套软电缆、安装用电线和屏蔽电线、特殊用途护套软电缆、聚氯乙烯绝缘阻燃/耐火电缆等产品。 GB/T 5023.3-2008额定电压450/750V及以下聚氯乙烯绝缘电缆 第3部分:固…...

深入单例模式
1. 饿汉模式 饿坏了,上来就先实例化一个对象,好处是代码简单,坏处是这个对象后面如果一直用不到,就是个浪费。 public class A{ private static A a new A(); private A(){} public static A getInstance(){ return a; } } 2. 懒…...

MongoDB 单机和集群环境部署教程
目录 一、MongoDB 单机环境部署1. 环境准备2. 安装 MongoDB2.1 在 Ubuntu 上安装 MongoDB2.2 在 CentOS 上安装 MongoDB2.3 启动 MongoDB 服务2.4 验证 MongoDB 安装2.5 MongoDB 基本安全设置 3. 单机部署注意事项 二、MongoDB 集群环境部署1. 环境准备2. MongoDB Replica Set …...
【学习笔记】Day 20
一、进度概述 1、机器学习常识12-18,以及相关代码复现 二、详情 12、SVM(support vector machines,支持向量机) 实际上,支持向量机是一种二分类模型,它将实例的特征向量映射为空间中的一些点,…...

StringBuffer与StringBuilder 2024-8-21 22-13
目录 一、StringBuffer二、StringBuilder三、总结 一、StringBuffer StringBuffer是一个可变的字符序列,它的存在是为了解决频繁操作字符串时产生大量临时对象的问题。 构造方法: StringBuffer():创建一个空的字符串缓冲区,初始容…...

会声会影剪辑视频收费吗,会声会影最新破解版
会声会影2024:引领视频创作新时代的创新之旅** 在数字时代的浪潮中,视频创作已成为连接世界、表达创意的重要方式。随着技术的不断进步,一款名为“会声会影2024”的视频编辑软件横空出世,它不仅继承了前代产品的优秀传统…...

在Windows11强制开启copilot
在 Windows 11 上启用自带的基于 GPT-4 的 Copilot 功能。以下是具体步骤: 更新系统: 确保你的 Windows 11 系统已经更新到最新版本(23H2 或更高版本)。你可以在“设置” > “Windows 更新”中检查并安装最新更新。 更改区域和…...

基于Java的开源CMS有哪些推荐,各自特点是什么
最强大、最易用的CMS,向大家做一个简要介绍。 01 Alfresco Alfresco是一个开源的企业网站内容管理系统,它提供了文档管理、多人协作、记录管理、知识管理网页内容和图像管理等功能。它使用Spring、 Hibernate、 Lucene 和JSF等最新java技术构建了模…...

IPC进程通信以及网络通信
一、IPC 进程间通信方式 共享内存 //最高效的进程间通信方式 不需要把用户的东西再复制到内核 他们与内核进行绑定 共享内存: 1、是一块,内核预留的空间 2、最高效的通信方式 //避免了用户空间到内核空间的数据拷贝 IPC通信方式 ---操作流程类似的…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
)
2025.6.9总结(利与弊)
凡事都有两面性。在大厂上班也不例外。今天找开发定位问题,从一个接口人不断溯源到另一个 接口人。有时候,不知道是谁的责任填。将工作内容分的很细,每个人负责其中的一小块。我清楚的意识到,自己就是个可以随时替换的螺丝钉&…...

python读取SQLite表个并生成pdf文件
代码用于创建含50列的SQLite数据库并插入500行随机浮点数据,随后读取数据,通过ReportLab生成横向PDF表格,包含格式化(两位小数)及表头、网格线等美观样式。 # 导入所需库 import sqlite3 # 用于操作…...
