堆及其多种接口与堆排序的实现
我们本期来讲解堆结构
目录
堆的结构
堆的初始化
堆的销毁
堆的插入
向上调整算法
堆的删除
向下调整算法
取堆顶元素
判断堆是否为空
堆中元素个数
堆排序
向下调整与向上调整效率计算
Top-K问题
全部代码
堆的结构
堆是一种用数组模拟二叉树的结构
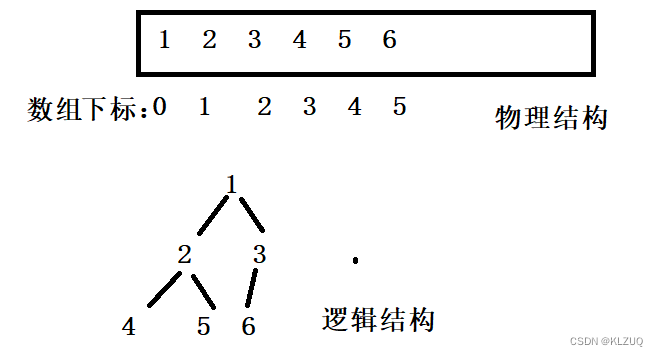
逻辑结构是我们想象出来的,物理结构是实实在在存在的
因为是用数组来实现的,所以我们访问时访问的是下标,那怎么通过下标来对应关系呢?
孩子和父节点的关系为:parent=(child-1)/2,leftchild=parent*2+1,rightchild=parent*2+2
这样我们就可以将节点之间的关系对应起来了
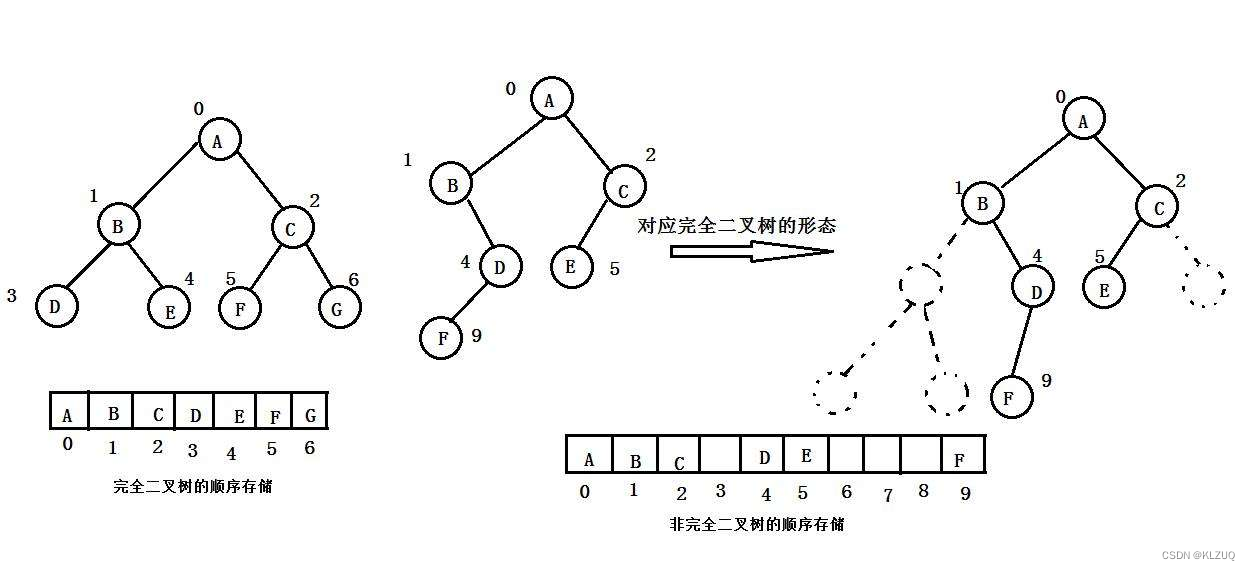
数组存储只适合存储完全二叉树,如果不是完全二叉树,就会出现很多空的地方,会有很大的空间浪费

我们主要掌握两种结构,一种是小堆,一种是大堆, 小堆是所有的父亲都小于等于孩子,大堆是所有父亲大于等于孩子
接着我们就来实现堆
在写堆之前,我们先来想一下,如果我们要在堆中插入数据该怎么办?
因为我是用数组实现,所以在插入时是需要考虑扩容的
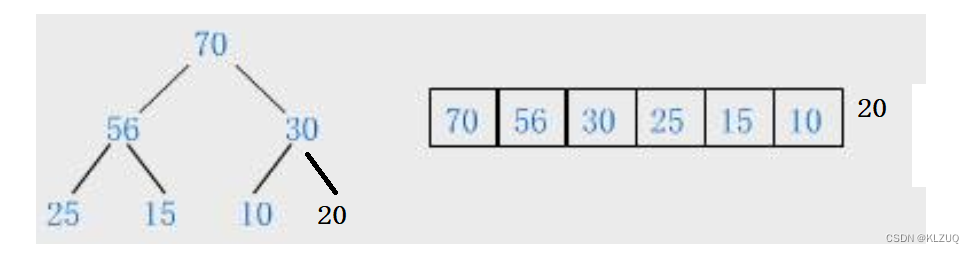 插入之后还要保证大堆还是大堆,小堆还是小堆
插入之后还要保证大堆还是大堆,小堆还是小堆
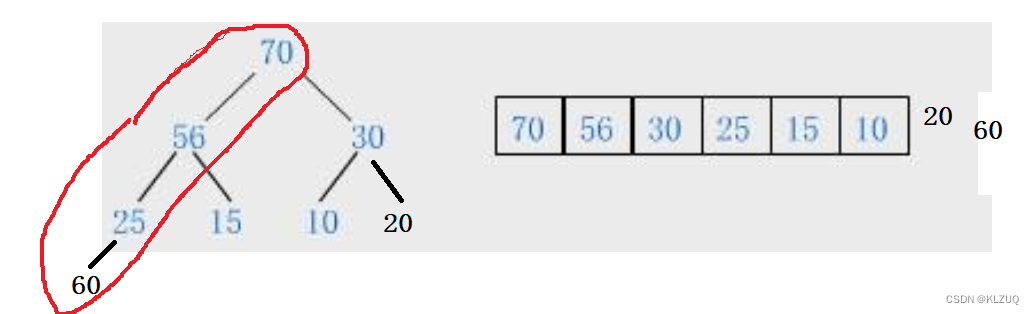
我们再次插入一个60的话,就需要和他的祖先进行交换了,我们通过下标计算出60的父亲是25,然后交换60和25,接着再次重复进行上面的步骤,交换60和56,这次才又变成了大堆
上面这个过程我们叫做向上调整,向上调整最多调整高度次
继续回到我们的堆来,我们来写堆的结构
typedef int HPDataType;
typedef struct Heap{HPDataType* a;int size;int capacity;
}HP;使用size来记录当前存储元素数量,capacity记录容量
堆的初始化
void HeapInit(HP* php) {assert(php);php->a = (HPDataType*)malloc(sizeof(HPDataType) * 4);if (php->a == NULL) {perror("malloc fail");return;}php->size = 0;php->capacity = 4;
}
我们传的是结构体的指针,所以一定不能为空,需要进行断言,接着我们给堆的数组开辟空间,初始大小根据需要来定,开辟是否成功我们判断一下,接着就是初始化其他元素了
堆的销毁
void HeapDestroy(HP* php) {assert(php);free(php->a);php->size = 0;php->capacity = 0;free(php);
}释放数组和空间即可
堆的插入
void HeapPush(HP* php, HPDataType x) {assert(php);if (php->size == php->capacity) {HPDataType* tmp = realloc(php->a,sizeof(HPDataType) * php->capacity * 2);if (tmp == NULL) {perror("realloc fail");return;}php->a = tmp;php->capacity *= 2;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}在插入前,我们要先判断是否需要扩容,接着插入并++size即可,但是我们上面说了,在插入后,要保证堆还是堆,我们需要向上调整,所以我们这里写出向上调整算法
向上调整算法
void Swap(int* x, int* y) {int tmp = *x;*x = *y;*y = tmp;
}
void AdjustUp(HPDataType* a,int child) {int parent = (child - 1) / 2;while (child > 0) {if (a[child] > a[parent]) {Swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}else {break;}}
}我们根据上面讲的例子就可以明白,这是一个循环,我们先找到父节点,接着进入循环,循环结束条件为child=0,即插入的元素走到堆顶,循环里我们对孩子和父亲进行比较,若父亲比孩子小,我们交换二者,接着让下标移动,否则退出循环
有了插入,我们对我们的堆进行一下测试

我们通过调试来看堆里的数据,发现为6,4,5,3,1,2,这就是我们的大堆,没有问题
堆的删除
堆的删除是删除堆里的一个元素,在写删除之前,我们仔细想想,我们是删除堆的哪里呢?
是头还是尾?删尾非常轻松,但是删尾没有意义,所以,堆的删除,是删除头,也叫删除堆顶
堆顶是一个堆里最大(最小)的数据,在实际中,无论是堆排序,还是topK,都是选大小,所以我们需要选出最值
那我们删除堆顶后,应该怎么办呢?举个例子,【40,10,15,1,2,3】这是一个堆,当我们把40删除后,我们是要把后续的数据向前挪动一位吗?答案是错误的
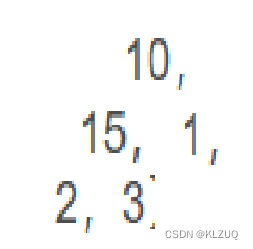
挪动删除有两大问题:1.效率低下,2.父子兄弟关系全乱了
原来10和15是兄弟,现在10变成了15的父亲,而且此时还不是大堆
我们要将堆顶的元素和堆中最后一个元素交换位置
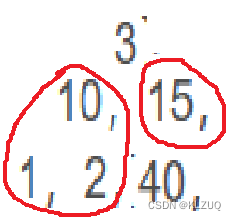
交换到末尾后,删除就简单了,而且我们此时再单看左子树和右子树,也都符合我们的要求,都是大堆,只有堆顶不满足,此时就需要一个向下调整算法
void HeapPop(HP* php) {assert(php); assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a,php->size,0);
}我们先看删除函数,我们交换堆顶与堆最后一个元素的位置,使size-1即可,接着就是向下调整
向下调整算法
void AdjustDown(HPDataType* a,int n, int parent) {int child = parent * 2 + 1;while (child < n) {if (child+1<n && a[child] < a[child + 1]) {child++;}if (a[child] > a[parent]) {Swap(&a[child], &a[parent]);parent=child;child = parent * 2 + 1;}else {break;}}
}与向上调整类似,也是一个循环,只不过这次我们是从头开始调整的,所以需要多一个参数来接收数组大小,向下调整是将堆顶这个小的数据放在他应该出现的位置,但和向上调整不同,父节点有两个孩子,我们选择和较大的孩子进行交换,不然可能会出现一些别的情况,我们先假设左孩子大,然后进行比较,如果这个节点有右孩子,并且右孩子更大,那么就将child更新,然后我们对父亲和孩子进行比较,如果孩子比父亲大,就交换,否则退出循环
向上调整和向下调整都是有前提的,向下调整的前提是左右子树都是大堆/小堆,向上调整的前提是除了child位置,前面的数据构成堆
取堆顶元素
HPDataType HeapTop(HP* php) {assert(php);return php->a[0];
}判断堆是否为空
bool HeapEmpty(HP* php) {assert(php);return php->size == 0;
}堆中元素个数
int HeapSize(HP* php) {assert(php);return php->size;
}
这三个函数都非常简单
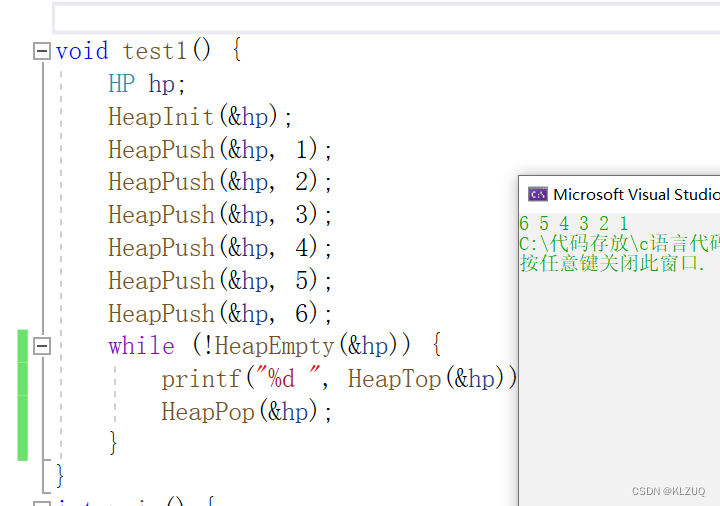
有了这些函数,我们来对堆进行一下测试
堆排序
有了上面的知识,我们接着来学习堆排序,刚才的操作,只能叫做有序打印,而不是排序,现在才是真正的排序
堆排序并不是我们写一个堆,将数据全部放入堆里,然后再取堆顶,这样做的话效率太低,我们还要写一个堆出来
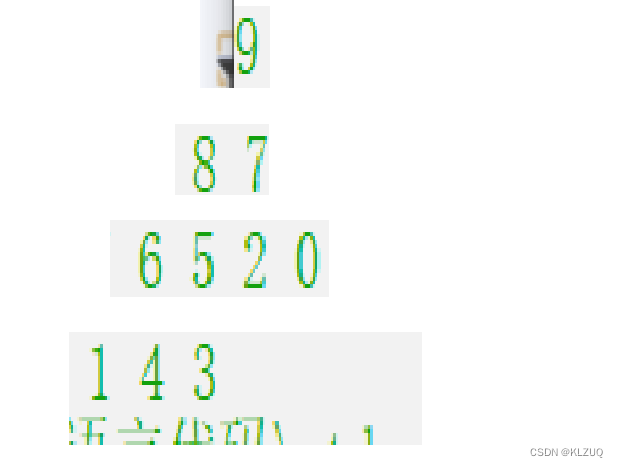
我们看我们的数组,虽然有了数据,但这些数据并不能构成堆,所以我们需要建堆
我们需要用向上调整来建堆,就是模拟插入的过程,即我们先把数组第一个元素看作堆里的元素,接着把第二个元素看作堆的元素插入,然后向上调整,接着是第三个元素,以此类推

这种建堆的时间复杂度为O(N*logN),此时我们的堆就建好了
通过调试我们可以看到
接着,我们要排升序的话,要建大堆还是小堆呢?
很大人可能会认为排升序要建小堆,但是建小堆就出问题了,小堆的话,第一个数排好了,剩下的数怎么办呢?就又变成了我们上面的挪动删除那样了
所以我们需要建大堆,我们将最大的数和最后一个元素交换位置,接着,我们不管最后一个数,将前面的数看作堆,然后向下调整,最多调整高度次就可以选出次大的数,时间复杂度为O(logN)
堆排序的时间复杂度为O(N*logN)
void HeapSort(int* a,int n) {//建堆,向上调整for (int i = 1; i < n; i++) {AdjustUp(a, i);}int end = n - 1;while (end>0) {Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}堆排序写起来是很简单的,前提是有我们的向上调整和向下调整

排降序的话建小堆即可
我们的建堆还有一种办法,是使用向下调整建堆,这种更常用,我们要从倒数第一个非叶子节点开始调整,因为调整叶子节点没意义

我们从6这个节点开始向下调整,6是尾节点的父亲,我们可以通过计算得到,调整完6后,我们要调整7, 6往前走一步就到了7,我们找到7这个节点左右孩子大的那个,就是9,然后交换9和7接着调整5,交换8和5,以此类推,最终9到达了堆顶
向下调整的效率是比向上调整高的,并且我们只需要写一个向下调整,不需要写向上调整就可以完成堆排序
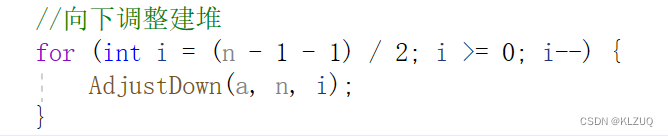
n-1是最后一个数的下标,再-1除以2是求父亲节点
接着我们来对比向上调整和向下调整的效率
向下调整与向上调整效率计算
向上调整建队的时间复杂度为O(N*longN),向下调整为O(N)
下面我们进行证明
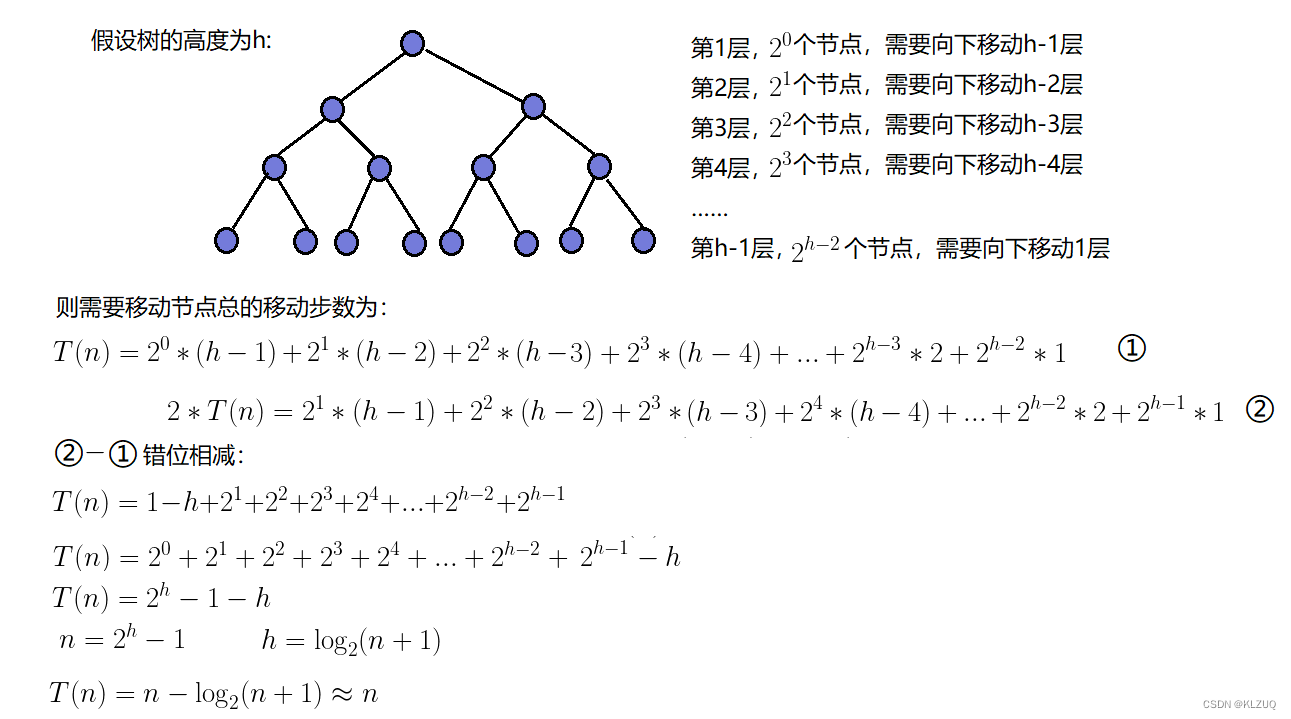
我们向下调整,是从倒数第二层开始调整,假设高度为h,倒数第二层节点数为2^(h-2)
我们用T(N)表示建堆的总次数
倒数第二层最坏需要调整1次,举个例子

我们的这个堆里,倒数第二层里的7需要和最后一层的9进行交换,所以是调整1次,在最坏的情况下,倒数第二层的所有节点都需要和他的孩子进行交换
所以倒数第二层的总调整次数为2^(h-2)*1
倒数第三层总调整次数为2^(h-3)*2
......
第二层总调整次数为2^1*(h-2)
第一层需要调整2^0*(h-1)
T(N)=2^(h-2)*1+2^(h-3)*2+......+2^1*(h-2)+2^0*(h-1)
这是一个等差乘以等比,我们要用错位相减法来计算
两边同时乘以2后变成:2*T(N)=2^(h-1)*1+2^(h-2)*2+......+2^2*(h-2)+2^1*(h-1)
接着我们进行相减,得到:T(N)=2^(h-1) + 2^(h-2)+2^(h-3)+...+ 2^2+2^1 - 2^0*(h-1)
最后的 - 2^0*(h-1),我们化解为 -(2^0-h),原理为2^0是1,我们不写,就变成了h-1,1又可以写成2^0
此时T(N)=2^(h-1) + 2^(h-2)+2^(h-3)+...+ 2^2+2^1+2^0 -h
前面的是是等比数列,计算结果为2^h-1,所以T(N)=2^h-1-h
如果这棵数有N个节点,那么2^h-1=N,N也就是数组大小,所以T(N)的前面是N,h是longN
所以向下调整的时间复杂度为O(N-longN),longN可以忽略不记,所以时间复杂度为O(N)
分开看就是每一层的节点数乘以向下调整多少次,然后加起来
接着我们看向上调整建堆
T(N)=2^1*1 + 2^2*2 + ... + 2^(h-2)*(h-2) + 2^(h-1)*(h-1)
我们分析一下,2^1*1代表第2层节点数乘以调整次数1次,第二层有两个节点,我们是模拟插入,即先插入一个,这个节点有可能和第一层的节点进行交换,接着插入第二个,第二个节点也可能和第一层的节点交换,交换次数最多为1,其他的以此类推
接着我们再用错位相减法计算
2*T(N)=2^2*1 + 2^3*2 + ... +2^(h-2)*(h-3) + 2^(h-1)*(h-2) + 2^(h)*(h-1)
相减得到T(N)= -2^1 - 2^2 -2^3 - ...... -2^(h-2) - 2^(h-1) +2^(h)*(h-1)
2^(h)*(h-1)分解变为 -2^h + 2^h*h,不分解也可以
最终得到T(N)= - 2^h+2 + 2^h*h - 2^h
又N=2^h-1,T(N)最后左边是N ,中间是N*longN,右边也是N,即时间复杂度为O((longN-2)*N)
也就是N*longN
所以向上调整的效率是比向下调整的效率要低的,综上,我们的堆排序用向下调整就行
Top-K问题
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
1. 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素
我们要找出N个数里最大的前K个,我们可以建N个大堆,然后pop k次就行
那假设N很大呢?比如N为100亿
此时数据在内存存不下,数据是在磁盘文件里的,要解决这个问题,就有人想出了这样的一个方法
我们前k个数据建小堆,遍历剩下的数据,如果这个数据比堆顶数据要大,就替代他进堆,向下调整,最后这个小堆的数据就是最大的前k个
这个思想是不是非常巧妙?最大的前k个来了一定比堆顶大,就可以进堆,如果我们建大堆的话,就有可能有一个很大的数在堆顶,其他数就进不了堆了
void PrintTopK(const char* file, int k) {//1.用前k个元素建小堆int* topk = (int*)malloc(sizeof(int) * k);if (topk == NULL) {perror("malloc fail");return;}FILE* fout = fopen(file, "r");if (fout == NULL) {perror("fopen error");return;}//读前k个数据建堆for(int i=0;i<k;i++){fscanf(fout, "%d", &topk[i]);}for (int i = (k - 1-1)/2; i >=0; i--) {AdjustDown(topk, k, i);}//2.将剩下的n-k个元素依次与堆顶元素比较,满足条件进行替换int val = 0;int ret= fscanf(fout, "%d", &topk[i]);while (ret != EOF) {if (val > topk[0]) {topk[0] = val;AdjustDown(topk, k, 0);}ret = fscanf(fout, "%d", &val);}//打印数据for (int i = 0; i < k; i++) {printf("%d ", topk[i]);}printf("\n");free(topk);fclose(fout);
}假设数据在文件里,所以我们使用文件的方式来写这个函数,最后的打印数据大家根据需求来修改即可
以上即为本期全部内容,希望大家可以有所收获
最后附上全部代码
全部代码
//heap.h
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int HPDataType;
typedef struct Heap{HPDataType* a;int size;int capacity;
}HP;void HeapInit(HP* php);
void HeapPush(HP* php,HPDataType x);
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
bool HeapEmpty(HP* php);
int HeapSize(HP* php);
void HeapDestroy(HP* php);//heap.c
#include"heap.h"
void HeapInit(HP* php) {assert(php);php->a = (HPDataType*)malloc(sizeof(HPDataType) * 4);if (php->a == NULL) {perror("malloc fail");return;}php->size = 0;php->capacity = 4;
}void Swap(int* x, int* y) {int tmp = *x;*x = *y;*y = tmp;
}
void AdjustUp(HPDataType* a,int child) {int parent = (child - 1) / 2;while (child > 0) {if (a[child] > a[parent]) {Swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}else {break;}}
}void HeapPush(HP* php, HPDataType x) {assert(php);if (php->size == php->capacity) {HPDataType* tmp = realloc(php->a,sizeof(HPDataType) * php->capacity * 2);if (tmp == NULL) {perror("realloc fail");return;}php->a = tmp;php->capacity *= 2;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}void AdjustDown(HPDataType* a,int n, int parent) {int child = parent * 2 + 1;while (child < n) {if (child+1<n && a[child] < a[child + 1]) {child++;}if (a[child] > a[parent]) {Swap(&a[child], &a[parent]);parent=child;child = parent * 2 + 1;}else {break;}}
}void HeapPop(HP* php) {assert(php);assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a,php->size,0);
}HPDataType HeapTop(HP* php) {assert(php);return php->a[0];
}
bool HeapEmpty(HP* php) {assert(php);return php->size == 0;
}
int HeapSize(HP* php) {assert(php);return php->size;
}void HeapDestroy(HP* php) {assert(php);free(php->a);php->size = 0;php->capacity = 0;free(php);
}//test.c
#include"heap.h"
void AdjustUp(HPDataType* a, int child);
void Swap(int* x, int* y);
void AdjustDown(HPDataType* a, int n, int parent);
void test1() {HP hp;HeapInit(&hp);HeapPush(&hp, 1);HeapPush(&hp, 2);HeapPush(&hp, 3);HeapPush(&hp, 4);HeapPush(&hp, 5);HeapPush(&hp, 6);while (!HeapEmpty(&hp)) {printf("%d ", HeapTop(&hp));HeapPop(&hp);}
}void HeapSort(int* a,int n) {//建堆,向上调整/*for (int i = 1; i < n; i++) {AdjustUp(a, i);}*///向下调整建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--) {AdjustDown(a, n, i);}int end = n - 1;while (end>0) {Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}void PrintTopK(const char* file, int k) {//1.用前k个元素建小堆int* topk = (int*)malloc(sizeof(int) * k);if (topk == NULL) {perror("malloc fail");return;}FILE* fout = fopen(file, "r");if (fout == NULL) {perror("fopen error");return;}//读前k个数据建堆for(int i=0;i<k;i++){fscanf(fout, "%d", &topk[i]);}for (int i = (k - 1-1)/2; i >=0; i--) {AdjustDown(topk, k, i);}//2.将剩下的n-k个元素依次与堆顶元素比较,满足条件进行替换int val = 0;int ret= fscanf(fout, "%d", &topk[i]);while (ret != EOF) {if (val > topk[0]) {topk[0] = val;AdjustDown(topk, k, 0);}ret = fscanf(fout, "%d", &val);}//打印数据for (int i = 0; i < k; i++) {printf("%d ", topk[i]);}printf("\n");free(topk);fclose(fout);
}void test2() {int a[10] = { 2,1,5,7,6,8,0,9,4,3 };HeapSort(a, 10);for (int i = 0; i < 10; i++) {printf("%d ", a[i]);}
}
int main() {test2();return 0;
}如有错误,还请指正
相关文章:

堆及其多种接口与堆排序的实现
我们本期来讲解堆结构 目录 堆的结构 堆的初始化 堆的销毁 堆的插入 向上调整算法 堆的删除 向下调整算法 取堆顶元素 判断堆是否为空 堆中元素个数 堆排序 向下调整与向上调整效率计算 Top-K问题 全部代码 堆的结构 堆是一种用数组模拟二叉树的结构 逻辑结构是…...
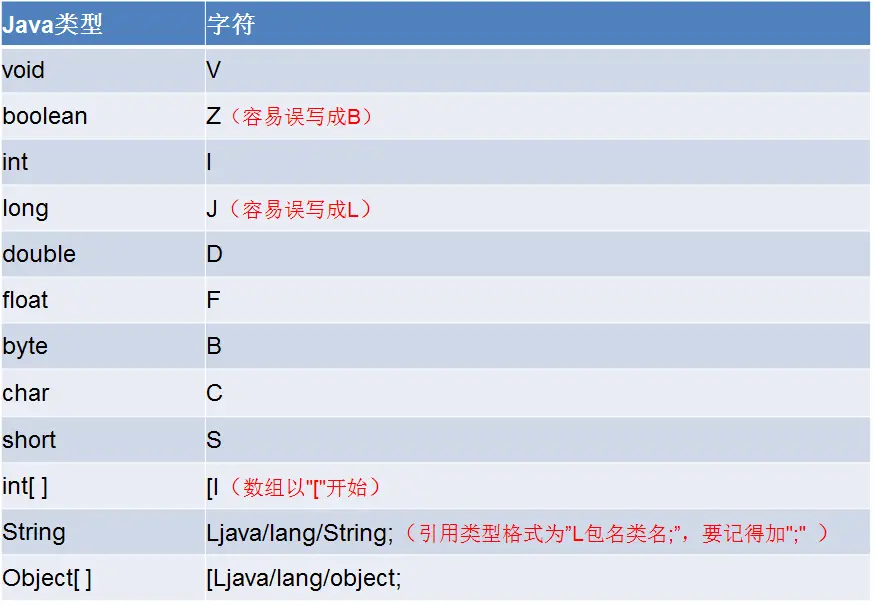
JNI原理及常用方法概述
1.1 JNI(Java Native Interface) 提供一种Java字节码调用C/C的解决方案,JNI描述的是一种技术。 1.2 NDK(Native Development Kit) Android NDK 是一组允许您将 C 或 C(“原生代码”)嵌入到 Android 应用中的工具,NDK描述的是工具集…...

【Docker】之docker-compose的介绍与命令的使用
🍁博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 文章目录docker-compose简介docker-compose基础…...
水果新鲜程度检测系统(UI界面+YOLOv5+训练数据集)
摘要:水果新鲜程度检测软件用于检测水果新鲜程度,利用深度学习技术识别腐败或损坏的水果,以辅助挑拣出新鲜水果,支持实时在线检测。本文详细介绍水果新鲜程度检测系统,在介绍算法原理的同时,给出Python的实…...

flask多并发
多线程 flask默认使用多进程处理请求,因此,是支持并发的。比如两个调用a.html和b.html, 请求a.html未运行完成,在浏览访问b.html不会阻塞。开两个不同浏览器,分别请求请求运行时间较长的a.html也不阻塞。只要不用一个…...

我用Python django开发了一个商城系统,已开源,求关注!
起始 2022年我用django开发了一个商城的第三方包,起名为:django-happy-shop。当时纯粹是利用业余时间来开发和维护这个包,想法也比较简单,Python语言做web可能用的人比较少,不一定有多少人去关注,就当是一个…...
大数据项目之数仓相关知识
第1章 数据仓库概念 数据仓库(DW): 为企业指定决策,提供数据支持的,帮助企业,改进业务流程,提高产品质量等。 DW的输入数据通常包括:业务数据,用户行为数据和爬虫数据等 ODS: 数据…...

RK3588平台开发系列讲解(视频篇)RTP H264 码流打包详解
平台内核版本安卓版本RK3588Linux 5.10Android 12文章目录 一、单 NALU 封包方式二、组合封包方式三、分片封包方式沉淀、分享、成长,让自己和他人都能有所收获!😄 📢 H264 码流是放在 RTP 的有效载荷部分的。因此有效载荷前面的 RTP 头部跟码流本身是没有关系的,所以我…...

realloc的补充 柔性数组
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章,「初学」C 🔥座右铭:“不要等到什么都没有了,才下…...
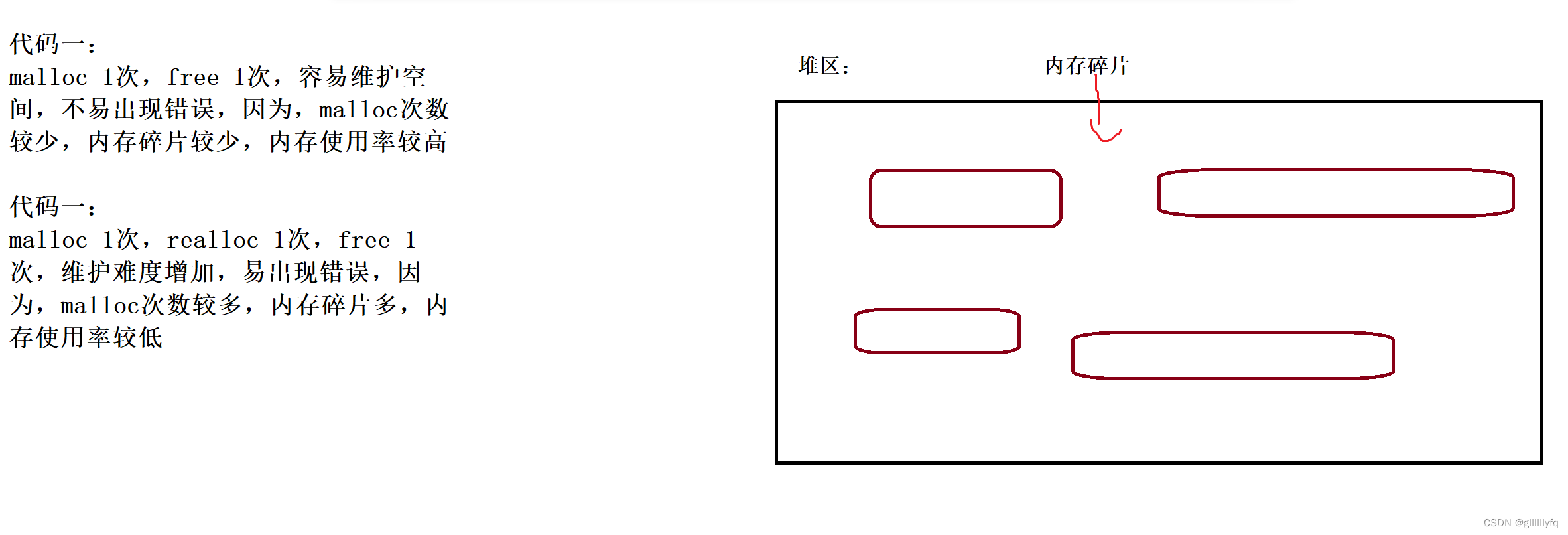
【C语言】柔性数组
柔性数组1. 柔性数组介绍2. 柔性数组特点3. 用例3.1 代码一:3.2 代码二:4. 柔性数组优势:1. 柔性数组介绍 也许你从来没有听说过柔性数组(flexible array)这个概念,但是它确实是存在的。 C99 中,…...
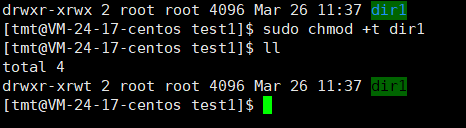
【Linux】权限详解
前言首先我们先来看一下权限的概念:在多用户计算机系统的管理中,权限(privilege)是指某个特定的用户具有特定的系统资源使用权力,像是文件夹,特定系统指令的使用或存储量的限制。通常,系统管理员…...

Android 之 打开相机 打开相册
Android 之 打开系统摄像头拍照 打开系统相册,并展示1,清单文件 AndroidManifest.xml<uses-permission android:name"android.permission.INTERNET" /><!--文件读取权限--><uses-permission android:name"android.permiss…...

C语言数据结构初阶(8)----栈与队列OJ题
CSDN的uu们,大家好。这里是C语言数据结构的第八讲。 目标:前路坎坷,披荆斩棘,扶摇直上。 博客主页: 姬如祎 收录专栏:数据结构与算法栈与队列的知识点我➡➡队列相关点我➡➡栈相关2. 用栈实现队列原题链接…...

JavaScript——原型对象
JavaScript——原型对象专题 文章目录JavaScript——原型对象专题1. 原型对象2. 原型对象的this指向3. 案例4. constructor属性5. 对象原型6. 总结7. 原型继承8. 原型链由先前的学习可知,构造函数实例创建的对象彼此独立、互不影响,很好的体现了面向对象…...
网络安全 2023 年为什么如此吃香?事实原来是这样....
前言由于我国网络安全起步晚,所以现在网络安全工程师十分紧缺。俗话说:没有网络安全就没有国家安全为什么选择网络安全?十四五发展规划建议明确提出建设网络强国,全面加强网络安全保障体系和能力建设,加强网络文明建设,…...

(源码篇02)webpack5中的事件调度系统和NormalModuleFactary核心逻辑
1. 书接上回,从 this.factorizeQueue.add(options, callback); 开始 不是很清楚上下文的兄弟,可以去看下我之前写的 (源码篇01)浅析webpack5中Compiler中重要的hook调用过程。 此文比较干,各位读者开始阅读前…...
做了啥?)
Vue2.x源码:new Vue()做了啥?
vue源码版本vue2.5.2 new Vue()做了啥? new Vue()会执行_init方法,而_init方法在initMixin函数中定义。 src/core/instance/index.js文件中定义了Vue function Vue (options) {this._init(options) }initMixin(Vue) stateMixin(Vue) eventsMixin(Vue) lifecycl…...

WinForm | C# 弹出简易的消息提示框 (仿Android Toast消息提示)
ApeForms Toast消息提示 文章目录ApeForms Toast消息提示前言方法原型及参数释义消息驻留延时消息弹出模式队列模式抢占模式复用模式UI库安装与使用获取示例源码前言 在使用手机的时候经常会见到屏幕的中下方会弹出消息提示框,它就是Toast,以下是百度百…...

1、DRF实战总结:DRF特点、序列化与RESTful API规范
Django这种基于MVC开发模式的传统框架,非常适合开发基于PC的传统网站,因为它同时包括了后端的开发(逻辑层、数据库层) 和前端的开发(如模板语言、样式)。现代网络应用Web APP或大型网站一般是一个后台,然后对应各种客户端(iOS, android, 浏览…...

SIP协议及其简单介绍
SIP协议及其简单介绍概述流程SIP流程两台设备建立会话原理使用场景概述 SIP(Session Initiation Protocol,会话初始化协议)是一个应用层协议,用于在互联网上创建、修改和终止多媒体会话。SIP是一个客户端/服务器协议,…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
