自行车制造5G智能工厂工业物联数字孪生平台,推进制造业数字化
在当今这个日新月异的数字化时代,制造业正经历着前所未有的变革,自行车制造5G智能工厂工业物联数字孪生平台的兴起,无疑是这场转型浪潮中一股强劲力量。自行车制造5G智能工厂工业物联数字孪生平台的成功应用,不仅仅是技术上的突破,更是对传统制造业发展模式的深刻变革。它标志着制造业正逐步摆脱对人力和资源的过度依赖,向更加高效、智能、可持续的方向发展。
提升产业竞争力。通过数字化转型,自行车制造企业能够大幅提升生产效率,降低运营成本,提高产品质量和创新能力,从而在激烈的市场竞争中占据有利地位。促进产业升级。数字化转型推动了自行车制造产业链的上下游企业共同升级,形成了更加紧密、协同的产业生态。这不仅有助于提升整个产业链的竞争力,还为产业的新旧动能转换提供了有力支撑。

推动绿色制造。智能制造技术的应用有助于减少生产过程中的资源消耗和环境污染,实现绿色制造。通过精准控制生产过程和优化能源管理,自行车制造企业能够显著降低碳排放,为可持续发展贡献力量。满足个性化需求。在数字化转型的背景下,自行车制造企业能够更加灵活地应对市场变化,快速响应消费者个性化需求。巨蟹数科通过数字孪生技术和工业物联网的支持,企业可以实现小批量、多品种的生产模式,为消费者提供更加丰富的选择。
自行车制造5G智能工厂工业物联数字孪生平台的出现,是制造业数字化转型的一个重要里程碑。它不仅为自行车制造行业带来了前所未有的发展机遇,也为整个制造业的转型升级提供了宝贵的经验和启示。随着技术的不断进步和应用的不断深化,我们有理由相信,未来的制造业将更加智能、高效、绿色和可持续。在这个过程中,自行车制造企业将扮演重要角色,引领制造业向更高水平迈进。
相关文章:

自行车制造5G智能工厂工业物联数字孪生平台,推进制造业数字化
在当今这个日新月异的数字化时代,制造业正经历着前所未有的变革,自行车制造5G智能工厂工业物联数字孪生平台的兴起,无疑是这场转型浪潮中一股强劲力量。自行车制造5G智能工厂工业物联数字孪生平台的成功应用,不仅仅是技术上的突破…...

一文彻底搞懂Transformer - FFNN(前馈神经网络)
Transformer 神经网络: 神经网络(Neural Networks)是一种模仿生物神经网络的结构和功能的数学或计算模型。它由大量的人工神经元(也称为节点或处理单元)相互连接而成,这些神经元之间通过带有权重的连接进行…...

SpringCloud Gateway及 Springboot 服务 跨域配置
SpringCloud Gateway 跨域配置 配置文件 #跨域支持 spring.cloud.gateway.globalcors.cors-configurations.[/**].allowed-headers[0]* spring.cloud.gateway.globalcors.cors-configurations.[/**].allowed-methods[0]* spring.cloud.gateway.globalcors.cors-configuration…...

【Solidity】安全与校验
信息传输 发送方 A: 计算消息 message 的哈希值 H:hash(message) H 私钥 privateKey ➕ 哈希值 H 🟰 签名 signature:signature sign(H, privateKey) 将消息 message 和签名 signature 发送给 B 接收方 B: 计算…...
黑神话悟空四十二项修改器 v1.0
软件简介 黑神话悟空四十二项修改器由风灵月影精心打磨,为《黑神话悟空》这款备受瞩目的游戏量身定制。这款修改器界面简洁、体积小巧、功能强大,它致力于为玩家提供便捷的游戏体验,让您能够根据个人喜好和需求,轻松调整游戏内的…...
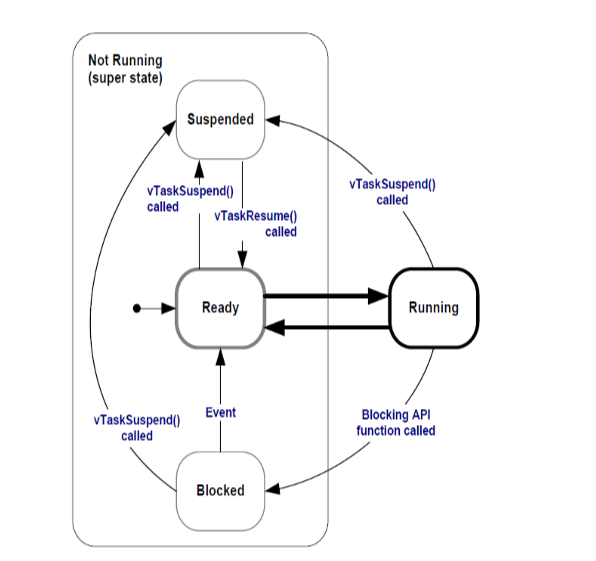
RM电控RTOS
OS即(operating system)操作系统,比如我们常用的windows系统,mac系统,android系统,ios系统,linux系统等,都属于操作系统。操作系统的本质是一个特殊的软件,它直接管理硬件…...

Arduino开源四足蜘蛛机器人制作教程
视频教程:手把手叫你做四足蜘蛛机器人——1零件介绍_哔哩哔哩_bilibili 一、项目介绍 1.1 项目介绍 Arduino主控,图形化编程,趣味学习 Arduino nano开发板舵机扩展底板 4.8V可充电电池,支持Arduino C语言编程和米思齐图形化编程…...
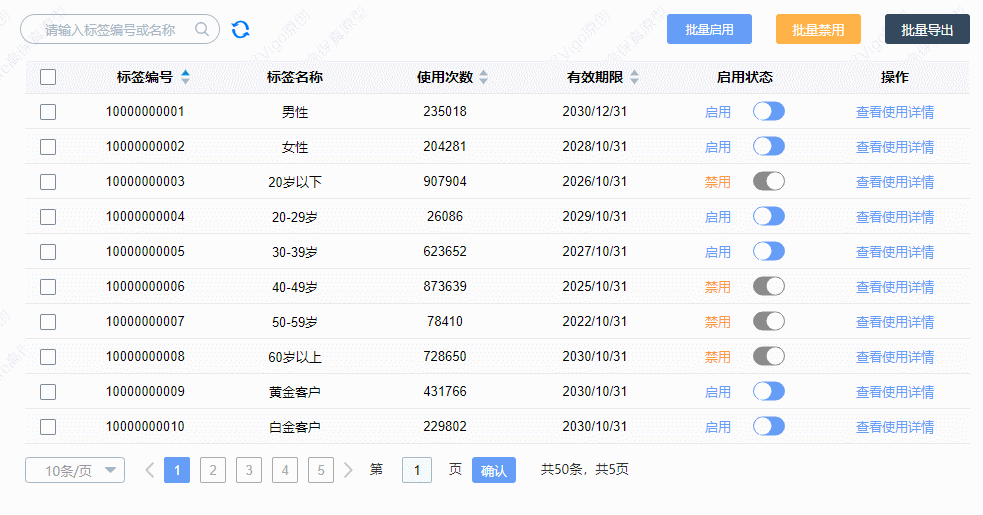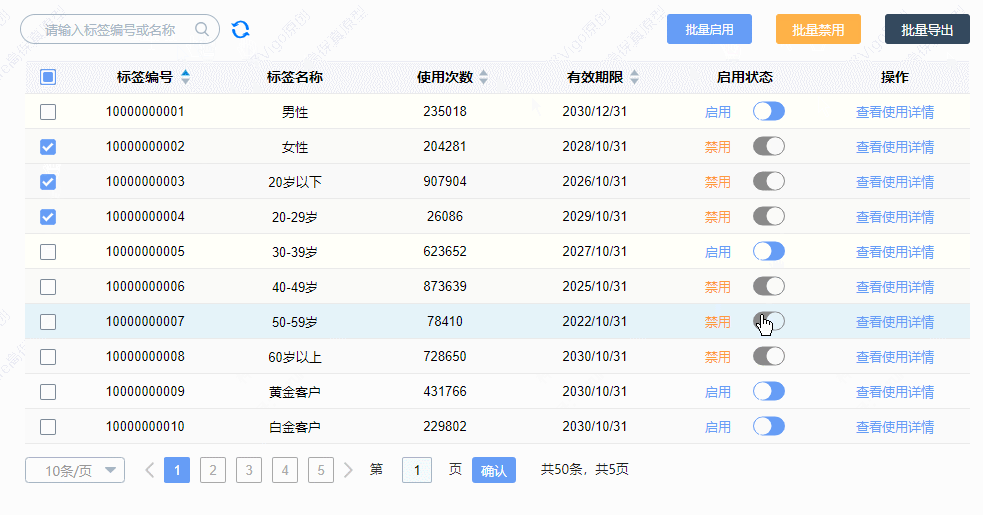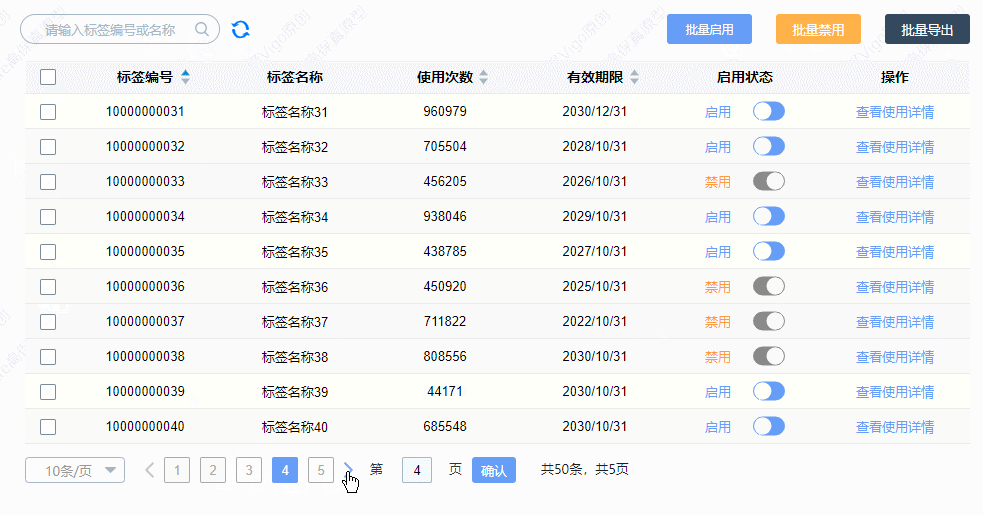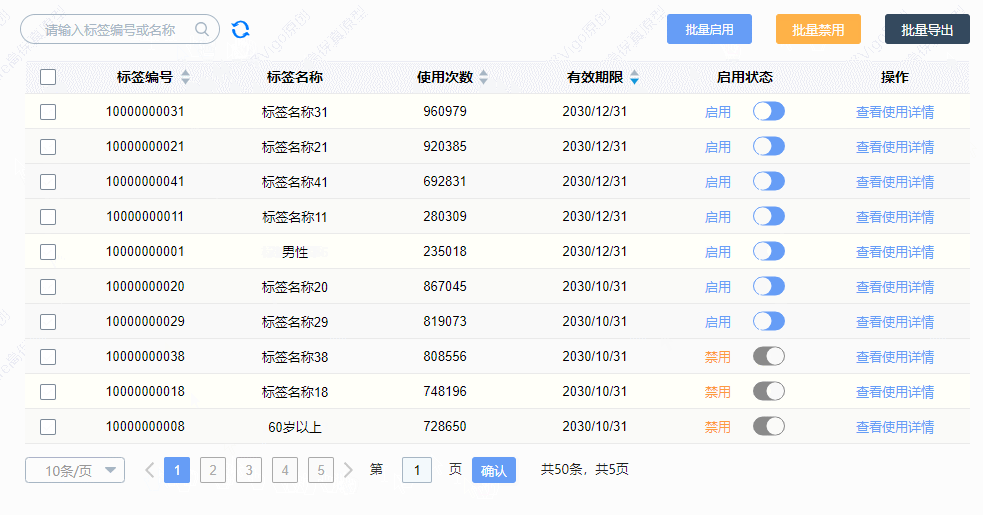
【Axure高保真原型】中继器表格——标签使用情况案例
今天和大家分享中继器表格——标签使用情况案例的原型模板,效果包括: 模糊搜索——输入标签编号或者标签名称,可以快速查找对应的数据 排序——点击排序按钮,可以按升序或降序排列 分页——点击上拉列表,可以选择表格…...

ABAP字符串反转 and 寻找字符所在位置 and 根据数量汇总时把数量转为非数值类型
1.字符串反转 and 寻找字符所在位置 LOOP AT gt_wlmc ASSIGNING FIELD-SYMBOL(<fs_wlmc>). "遍历内表<fs_wlmc>-matnr <fs_wlmc>-matnr(8).DATA: l_output TYPE char50,v_off2 TYPE i,str TYPE i,str2 TYPE i.CALL FUNCTION STRING_REVERS…...

【机器学习第十二章——计算学习理论】
机器学习第十二章——计算学习理论 12.计算学习理论12.1 基础知识12.1 可能学习近似正确假设(PAC)12.3 有限假设空间12.4 VC维 12.计算学习理论 12.1 基础知识 从理论上刻画了若干类型的机器学习问题中的困难和若干类型的机器学习算法的能力 这个理论要…...

Docker私人学习笔记
俗话说“好记性不如烂笔头”,编程的海洋如此的浩大,养成做笔记的习惯是成功的一步! 此笔记主要是antlr4.13版本的笔记,并且笔记都是博主自己一字一字编写和记录,有错误的地方欢迎大家指正。 一、基础概念:…...

谷粒商城实战笔记-233~235-商城业务-认证服务-单点登录流程-原理
文章目录 一,场景二,单点登录流程 一,场景 包含以下三节的内容: 一,233-商城业务-认证服务-单点登录流程-1二,233-商城业务-认证服务-单点登录流程-2三,233-商城业务-认证服务-单点登录流程-3…...

机器学习在旅游业的革新之旅
机器学习在旅游业的革新之旅 随着科技的飞速发展,尤其是人工智能(AI)技术的广泛应用,各个行业都迎来了前所未有的变革。其中,旅游业作为全球经济的重要支柱之一,更是受益匪浅。机器学习(Machin…...
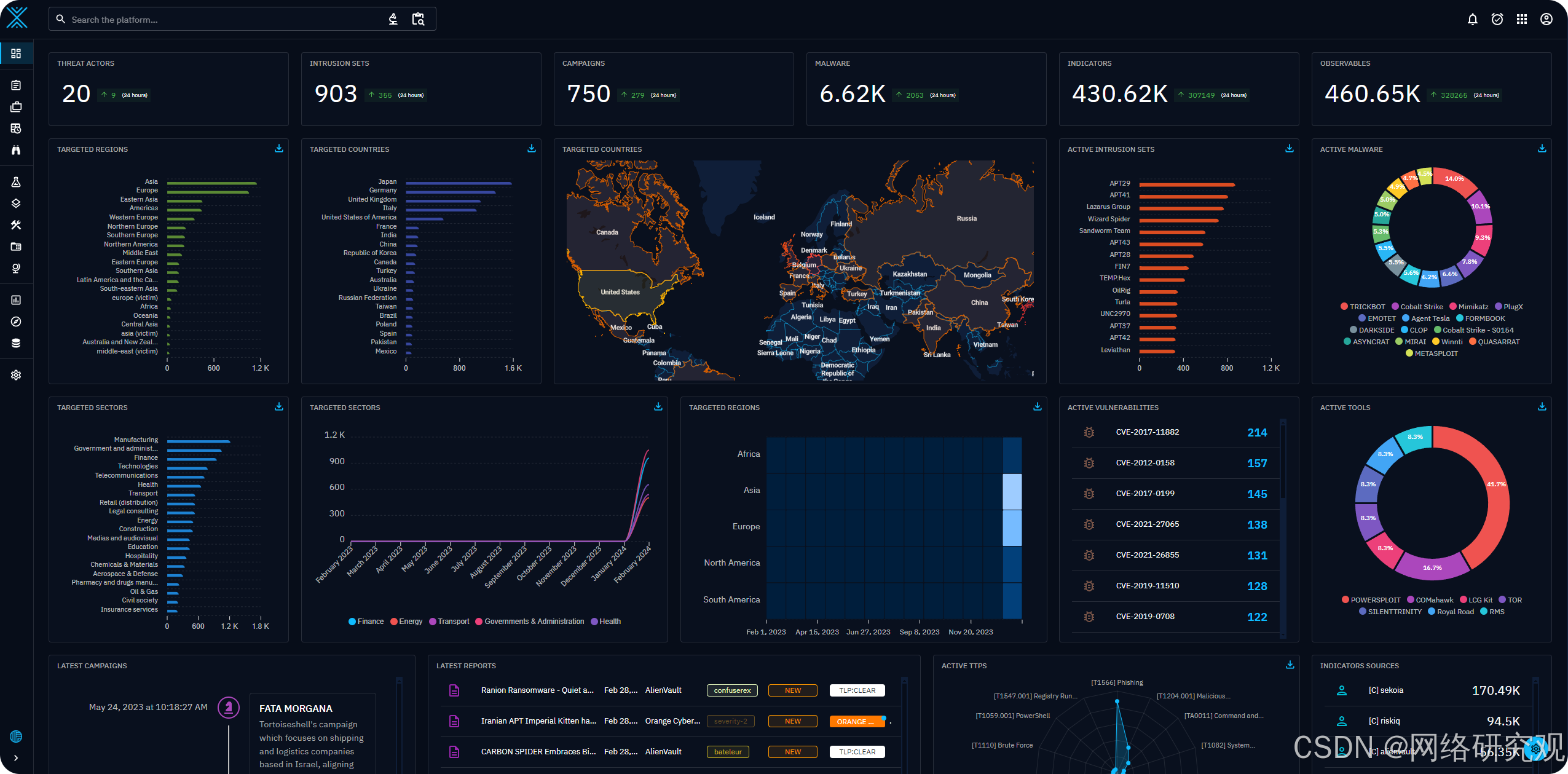
OpenCTI:开源网络威胁情报平台
OpenCTI 是一个开源平台,旨在帮助组织管理其网络威胁情报 (CTI) 数据和可观察数据。 该平台由 Filigran 开发,使用基于 STIX2 标准的知识模式构建数据。 它采用现代 Web 应用程序架构,配备 GraphQL API 和用户友好的前端。 OpenCTI 与 MIS…...

linux shell 脚本 let 数学计算
linux shell 脚本 let 数学计算 http://www.codebaoku.com/it-shell/ let命令中的算术表达式必须用双引号括起来,以避免解释器对特殊字符进行处理。 在变量的计算中,不需要使用$符号来表示变量, #!/bin/shweek_daydate %u echo $week_day…...
mp3和mp4的区别是什么?怎么把mp3转成mp4?(全)
在生活中我们或多或少会听到“mp3”和“mp4”,那么什么是mp3和mp4呢?mp3和mp4的区别是什么?mp3是一种音频压缩技术,旨在在不显著牺牲音质的前提下减小音频文件的体积,使其适用于音乐和其他音频内容的存储与传输。相比之…...

合并params和query参数
场景:三级分类只有query参数,搜索框使用params参数。为了解决这个问题,文中在typeNav的index.vue和Head/index.vue分别进行了判断和处理,确保在不同的路径下合并params和query参数能正确合并并传递。 如何当点击联动框时跳转到se…...

[数据集][目标检测]工程机械车辆检测数据集VOC+YOLO格式3189张10类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):3189 标注数量(xml文件个数):3189 标注数量(txt文件个数):3189 标注…...

构建域名服务器-BIND:Linux端的安装过程及配置文件详解
文章目录 构建域名服务器工具-BINDBIND的安装BIND配置文件详解1. /etc/named.conf:2. /etc/named.rfc1912.zones:3. /var/named/named.localhost:4./etc/logrotate.d/named5./etc/named.iscdlv.key6./etc/named.root.key7./etc/rndc.conf8./e…...

linux查询目录文件基础操作
基础命令 展示所有目录 ls 长格式列出(显示文件权限、所有者、大小和最后修改时间): ls -l 忽略大小写查询 ls | grep -i name 查找特定名称的文件: find /path/to/search -name "filename" 忽略大小写查找文件&#…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...
