机器学习——决策树,朴素贝叶斯
一.决策树
- 决策树中的基尼系数(Gini Index)是用于衡量数据集中不纯度(或混杂度)的指标。基尼系数的取值范围在0到0.5之间,其中0表示数据完全纯(同一类别),0.5表示数据完全混杂。
基尼系数的公式
对于一个节点,基尼系数的计算公式为:
G i n i ( p ) = 1 − ∑ i = 1 n p i 2 Gini(p) = 1 - \sum_{i=1}^{n} p_i^2 Gini(p)=1−i=1∑npi2
其中:
- ( n ) 是类别的总数。
- ( p_i ) 是属于类别 ( i ) 的样本所占的比例。
计算步骤
假设在某个节点上有 ( m ) 个样本,分别属于 ( n ) 个不同的类别,类别 ( i ) 的样本数量为 ( c_i ),那么:
p i = c i m p_i = \frac{c_i}{m} pi=mci
将 ( p_i ) 带入基尼系数公式,可以得到:
G i n i ( p ) = 1 − ∑ i = 1 n ( c i m ) 2 Gini(p) = 1 - \sum_{i=1}^{n} \left( \frac{c_i}{m} \right)^2 Gini(p)=1−i=1∑n(mci)2
示例计算
假设某个节点上有以下数据分布:
- 类别 A: 4 个样本
- 类别 B: 6 个样本
- 类别 C: 10 个样本
总样本数量 ( m = 4 + 6 + 10 = 20 )。
每个类别的比例为:
-
类别 A:
p A = 4 20 = 0.2 p_A = \frac{4}{20} = 0.2 pA=204=0.2 -
类别 B:
p B = 6 20 = 0.3 p_B = \frac{6}{20} = 0.3 pB=206=0.3 -
类别 C:
p C = 10 20 = 0.5 p_C = \frac{10}{20} = 0.5 pC=2010=0.5
基尼系数计算如下:
G i n i ( p ) = 1 − ( 0. 2 2 + 0. 3 2 + 0. 5 2 ) = 1 − ( 0.04 + 0.09 + 0.25 ) = 1 − 0.38 = 0.62 Gini(p) = 1 - (0.2^2 + 0.3^2 + 0.5^2) = 1 - (0.04 + 0.09 + 0.25) = 1 - 0.38 = 0.62 Gini(p)=1−(0.22+0.32+0.52)=1−(0.04+0.09+0.25)=1−0.38=0.62
该节点的基尼系数为 0.62,表示数据在这个节点上具有一定的不纯度。基尼系数越小,节点越纯,因此在构建决策树时,通常选择基尼系数最小的划分方式来分割数据。
DecisionTreeClassifier是scikit-learn库中用于分类任务的决策树模型。决策树通过一系列决策规则将数据分成不同的类别。
1. criterion(默认值:"gini")
- 含义:用于衡量数据分裂质量的指标。
- 取值:
"gini":使用基尼不纯度(Gini impurity)作为分裂的标准。基尼不纯度是衡量集合中随机选择的两个元素属于不同类别的概率。"entropy":使用信息增益(Information Gain),基于信息熵(Entropy)来选择分裂点。
2. splitter(默认值:"best")
- 含义:选择每次分裂的策略。
- 取值:
"best":在所有特征中选择最佳分裂点。"random":随机选择特征的最佳分裂点。
3. max_depth(默认值:None)
- 含义:控制决策树的最大深度。树的深度越大,模型越复杂。
- 取值:
None:树会一直生长,直到所有叶节点是纯的,或者每个叶节点包含少于min_samples_split个样本。int:树的最大深度。较小的值防止过拟合,较大的值允许树更复杂。
4. min_samples_split(默认值:2)
- 含义:内部节点再分裂所需的最小样本数。
- 取值:
int:指定最小样本数的具体值。float:以比例形式指定最小样本数(即一个0到1之间的小数)。
5. min_samples_leaf(默认值:1)
- 含义:叶节点所需的最小样本数。可以防止模型生成包含少量样本的叶节点。
- 取值:
int:指定最小样本数的具体值。float:以比例形式指定最小样本数。
6. min_weight_fraction_leaf(默认值:0.0)
- 含义:叶节点所需的最小样本权重的比例。
- 取值:
float:介于0到1之间,通常用于处理样本权重。
7. max_features(默认值:None)
- 含义:在每次分裂时考虑的最大特征数量。
- 取值:
None:使用所有特征。int:使用指定数量的特征。float:使用特定比例的特征。"auto":等同于sqrt(n_features)。"sqrt":等同于sqrt(n_features)。"log2":等同于log2(n_features)。
8. random_state(默认值:None)
- 含义:控制随机数生成器的种子,以便结果可以复现。
- 取值:
None:随机种子。int:指定种子。
9. max_leaf_nodes(默认值:None)
- 含义:限制树的最大叶节点数。设置此参数会优先于
max_depth。 - 取值:
None:不限制叶节点数量。int:最大叶节点数量。
10. min_impurity_decrease(默认值:0.0)
- 含义:节点分裂后不纯度下降的最小值。如果不纯度下降小于这个值,节点将不再分裂。
- 取值:
float:一个非负值。
11. class_weight(默认值:None)
- 含义:为不同类别指定权重,用于处理类别不平衡问题。
- 取值:
None:不调整类别权重。dict:根据指定字典中的权重调整类别。"balanced":根据类频率调整权重,权重与样本数量成反比。
12. ccp_alpha(默认值:0.0)
- 含义:复杂度剪枝参数,作为最小成本复杂度修剪的参数。增加此值将导致更简单的树。
- 取值:
float:一个非负值。越大越能剪枝。
示例代码
#决策树from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import accuracy_score# 1. 加载数据集
wine = load_wine()
X = wine.data
y = wine.target# 2. 标准化数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 3. PCA降维
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)# 4. 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_pca, y, test_size=0.3, random_state=32)# 5. 决策树预估器
nb = DecisionTreeRegressor()
nb.fit(X_train, y_train)# 6. 预测和评估
y_pred = nb.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)print(f"分类准确率: {accuracy:.2f}")- 控制树的复杂性:可以通过调整
max_depth、min_samples_split、min_samples_leaf、max_leaf_nodes等参数来控制决策树的复杂性,避免过拟合。 - 处理类别不平衡:使用
class_weight参数为不同类别指定权重。
二.朴素贝叶斯
朴素贝叶斯(Naive Bayes)是基于贝叶斯定理的一类简单而强大的分类算法。尽管它的假设比较强(特征之间条件独立),但在许多实际应用中效果非常好。下面是朴素贝叶斯算法的数学原理:
1. 贝叶斯定理
贝叶斯定理是朴素贝叶斯分类器的基础,用于计算后验概率。贝叶斯定理的公式如下:
P ( y ∣ X ) = P ( X ∣ y ) ⋅ P ( y ) P ( X ) P ( y ∣ X ) = P ( X ∣ y ) ⋅ P ( y ) P ( X ) P ( y ∣ X ) = P ( X ) P ( X ∣ y ) ⋅ P ( y ) P(y∣X)=P(X∣y)⋅P(y)P(X)P(y | X) = \frac{P(X | y) \cdot P(y)}{P(X)}P(y∣X)=P(X)P(X∣y)⋅P(y) P(y∣X)=P(X∣y)⋅P(y)P(X)P(y∣X)=P(X)P(X∣y)⋅P(y)P(y∣X)=P(X)P(X∣y)⋅P(y)
其中:
-
P ( y ∣ X ) P ( y ∣ X ) P ( y ∣ X ) P(y∣X)P(y | X)P(y∣X) P(y∣X)P(y∣X)P(y∣X)
是给定特征 XXX 时类别 yyy 的后验概率。
-
P(X∣y)P(X | y)P(X∣y) 是在类别 yyy 的条件下,特征 XXX 出现的概率,即似然度。
-
P(y)P(y)P(y) 是类别 yyy 的先验概率。
-
P(X)P(X)P(X) 是特征 XXX 的边际概率(用于归一化)。
2. 朴素假设
朴素贝叶斯模型做了一个关键的简化假设,即特征之间是条件独立的,这意味着给定类别 yyy 时,特征
X 1 , X 2 , … , X n X 1 , X 2 , … , X n X 1 , X 2 , … , X n X1,X2,…,XnX_1, X_2, \dots, X_nX1,X2,…,Xn X1,X2,…,XnX1,X2,…,XnX1,X2,…,Xn
是独立的。这一假设大大简化了后验概率的计算,使得模型易于实现且计算效率高。
在这种假设下,贝叶斯定理可以简化为:
P ( y ∣ X 1 , X 2 , … , X n ) ∝ P ( y ) ⋅ P ( X 1 ∣ y ) ⋅ P ( X 2 ∣ y ) ⋅ ⋯ ⋅ P ( X n ∣ y ) P ( y ∣ X 1 , X 2 , … , X n ) ∝ P ( y ) ⋅ P ( X 1 ∣ y ) ⋅ P ( X 2 ∣ y ) ⋅ ⋯ ⋅ P ( X n ∣ y ) P ( y ∣ X 1 , X 2 , … , X n ) ∝ P ( y ) ⋅ P ( X 1 ∣ y ) ⋅ P ( X 2 ∣ y ) ⋅ ⋯ ⋅ P ( X n ∣ y ) P(y∣X1,X2,…,Xn)∝P(y)⋅P(X1∣y)⋅P(X2∣y)⋅⋯⋅P(Xn∣y)P(y | X_1, X_2, \dots, X_n) \propto P(y) \cdot P(X_1 | y) \cdot P(X_2 | y) \cdot \dots \cdot P(X_n | y)P(y∣X1,X2,…,Xn)∝P(y)⋅P(X1∣y)⋅P(X2∣y)⋅⋯⋅P(Xn∣y) P(y∣X1,X2,…,Xn)∝P(y)⋅P(X1∣y)⋅P(X2∣y)⋅⋯⋅P(Xn∣y)P(y∣X1,X2,…,Xn)∝P(y)⋅P(X1∣y)⋅P(X2∣y)⋅⋯⋅P(Xn∣y)P(y∣X1,X2,…,Xn)∝P(y)⋅P(X1∣y)⋅P(X2∣y)⋅⋯⋅P(Xn∣y)
这意味着我们可以通过计算各个特征在每个类别下的条件概率,并将它们相乘来计算后验概率。
MultinomialNB()多项式朴素贝叶斯和GaussianNB()都是朴素贝叶斯(Naive Bayes)分类器的变种,适用于不同类型的数据。
1. MultinomialNB()–多项式朴素贝叶斯
MultinomialNB()是朴素贝叶斯分类器的一种,适用于多项式分布数据或者称为计数数据的分类问题。它假设特征是由一个多项分布生成的,这在文本分类和其他类型的分类任务中非常常见。
适用情况:
- 数据特征应为计数数据,如文档中单词出现的次数。
- 特征可以是整数计数,通常是非负的。
- 多项式朴素贝叶斯通常用于文本分类,其中特征向量表示单词出现的频率或者 TF-IDF 权重。
工作原理:
- 计算每个类别的条件概率,即给定类别下每个特征的概率分布。
- 使用贝叶斯定理计算后验概率,并结合各特征的条件概率,得出最终的分类结果。
#多项式朴素贝叶斯
from sklearn.datasets import load_wine
from sklearn.preprocessing import StandardScaler #标准化
from sklearn.preprocessing import MinMaxScaler#归一化
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
import numpy as npdata = load_wine()x= data.data# #标准化
# transfer = StandardScaler()
# x1 =transfer.fit_transform(x)# 2. 缩放数据到[0, 1]范围
scaler = MinMaxScaler()
x1 = scaler.fit_transform(x)#PCA降维
tr = PCA(n_components=0.89)
x2 = tr.fit_transform(x1)# 4. 将负值平移为非负值
x3 = x2- np.min(x2)x_train, x_test, y_train, y_test = train_test_split(x3, data.target,test_size=0.2,random_state=44)#MultinomialNB分类--多项式朴素贝叶斯
model = MultinomialNB()
model.fit(x_train,y_train)score = model.score(x_test,y_test)
print(score)
2. GaussianNB()
GaussianNB()是朴素贝叶斯分类器的另一种形式,适用于特征服从正态分布(Gaussian Distribution)的数据分类问题。
适用情况:
- 特征数据应为连续值,符合正态分布。
- 可以处理实数特征,如一些测量值或者物理量。
工作原理:
- 假设每个类别的特征值服从正态分布,通过计算每个类别下特征的均值和方差来估计类别条件概率分布。
- 使用贝叶斯定理计算后验概率,并结合特征的正态分布参数,得出最终的分类结果。
#朴素贝叶斯分类
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score# 1. 加载数据集
wine = load_wine()
X = wine.data
y = wine.target# 2. 标准化数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 3. PCA降维
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)# 4. 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_pca, y, test_size=0.3, random_state=42)# 5. 朴素贝叶斯分类
nb = GaussianNB()
nb.fit(X_train, y_train)# 6. 预测和评估
y_pred = nb.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)print(f"分类准确率: {accuracy:.2f}")
总结比较
-
数据类型:
MultinomialNB()适用于离散型特征,如计数数据。GaussianNB()适用于连续型特征,如实数数据。
-
假设:
MultinomialNB()假设特征是由多项分布生成的。GaussianNB()假设特征值服从正态分布。
-
应用场景:
MultinomialNB()在文本分类(如垃圾邮件分类)、推荐系统(基于用户行为的分类)等方面表现良好。GaussianNB()在数据特征服从正态分布的情况下表现良好,如一些传感器数据的分类或者健康检测领域。
相关文章:

机器学习——决策树,朴素贝叶斯
一.决策树 决策树中的基尼系数(Gini Index)是用于衡量数据集中不纯度(或混杂度)的指标。基尼系数的取值范围在0到0.5之间,其中0表示数据完全纯(同一类别),0.5表示数据完全混杂。 基…...

C语言基础(十)
编译预处理命令: 预编译命令在C语言中用于在编译前进行一些特定的处理和控制,帮助程序员更灵活地管理源代码和控制编译过程。 C语言常用的预编译命令: #include:用于包含头文件,将另一个文件的内容插入到当前文件中…...

人像比对-人证比对-人脸身份证比对-人脸身份证实名认证-人脸三要素对比-实人认证
人脸身份证实名认证是一种基于生物识别技术的身份验证方式,主要依托证件OCR识别技术、活体检测、人脸比对等技术手段,对用户身份信息真实性进行核验,确保用户为真人且为本人。以下是关于人脸身份证实名认证的详细解析: 一、认证流…...

Android 上下滑隐藏显示状态栏
一、DisplayPolicy类中监听滑动事件,然后发送广播事件 Android12类路径: frameworks/base/services/core/java/com/android/server/wm/DisplayPolicy.javamSystemGestures new SystemGesturesPointerEventListener(mUiContext, mHandler,new SystemGest…...

USBCAN-II/II+使用方法以及qt操作介绍
一.USBCAN-II/II介绍 USBCAN-II/II 是一款常用的 USB-CAN 转换器,广泛应用于汽车电子、工业自动化等领域。以下是使用该设备的一般步骤和方法: 1. 硬件连接 连接设备:将 USBCAN-II/II 的 USB 接口连接到计算机的 USB 端口。 连接 CAN 网络…...

笔记-系统规划与管理师-案例题-2022年-IT服务部署实施
【说明】 某大型企业去年信息化投入大,完成了重点核心业务系统的建设。由于应急相应预案制定得不充分并且未开展演练,出现了系统性故障时,部分关键的应用系统不可用且在12小时内未能完成恢复业务,给企业带来了较大损失。 为加强该…...

Kubernetes 清理资源常用的 Kubernetes 清理命
清理特定状态的 Pod: 清理 Evicted 状态的 Pod: kubectl get pods --all-namespaces -o wide | grep Evicted | awk {print $1,$2} | xargs -L1 kubectl delete pod -n清理 Error 状态的 Pod: kubectl get pods --all-namespaces -o wide | g…...

【数据结构初阶】二叉树--基本概念
hello! 目录 一、树 1.1 树的概念和结构 1.2 树的相关术语 1.3 树的表示 1.4 树形结构实际应用场景 二、二叉树 2.1 概念和结构 2.2 特殊的二叉树 2.2.1 满二叉树 2.2.2 完全二叉树 2.3 二叉树的存储结构 2.3.1 顺序结构 2.3.2 链式结构 …...

Pytorch添加自定义算子之(12)-开闭原则设计tensorrt和onnxruntime推理语义分割模型
一、开闭原则 开闭原则是SOLID原则中的一个,指的是尽量使用开放扩展,关闭修改的设计原则。 在C++中如何使用开闭原则导出动态库,可以按照以下步骤进行: 定义抽象基类:定义动态库中的抽象基类,该基类应该封装可扩展的接口。 实现派生类:实现基类的派生类,这些派生类将封…...

第二百零九节 Java格式 - Java数字格式类
Java格式 - Java数字格式类 以下两个类可用于格式化和解析数字: java.text.NumberFormatjava.text.DecimalFormat NumberFormat 类可以格式化一个数字特定地区的预定义格式。 DecimalFormat 类可以格式化数字以特定区域设置的自定义格式。 NumberFormat类的 getXXXInstance…...

LSI-9361阵列卡笔记
背景 要将raid0更改为JBOD直通模式 注意的点是要先将raid模式调整为JBOD之后重启机器,即可 备注:转换过程中硬盘中的数据未丢失。 步骤贴图 refer https://zhiliao.h3c.com/questions/dispcont/123250 https://blog.csdn.net/GreapFruit_J/article/…...

ArcGIS热点分析 (Getis-Ord Gi*)——基于地级市尺度的七普人口普查数据的热点与冷点分析
先了解什么是热点分析 ? 热点分析 (Getis-Ord Gi*) 是一种用于空间数据分析的技术,主要用于识别地理空间数据中值的聚集模式,可以帮助我们理解哪些区域存在高值或低值的聚集,这些聚集通常被称为“热点”或“冷点”,Gi* 统计量为…...

ASIACRYPT 2021
分类文章编号获奖论文1-3后量子密码4-9多方计算10-15物理攻击,泄露和对策16-21理论22-27公钥密码和鉴权密钥交换28-33高级加密和签名34-39对称密钥构建40-46量子安全47-53获奖论文54对称密码分析55-66增强型公钥加密和时间锁难题67-72同态加密和加密搜索73-77NIZK和SNARK78-80…...
C#学习之路day1
目录 一、概念:.net和c# 二、.net发展方向 三、.Net两种交互模式 四、创建项目 五、vs的组成部分 六、我的第一个C#程序 七、多个项目时启动项目的设置 八、注释 九、快捷键 一、概念:.net和c# 1、.net/dotnet :一般指.Net Framework框架&#…...
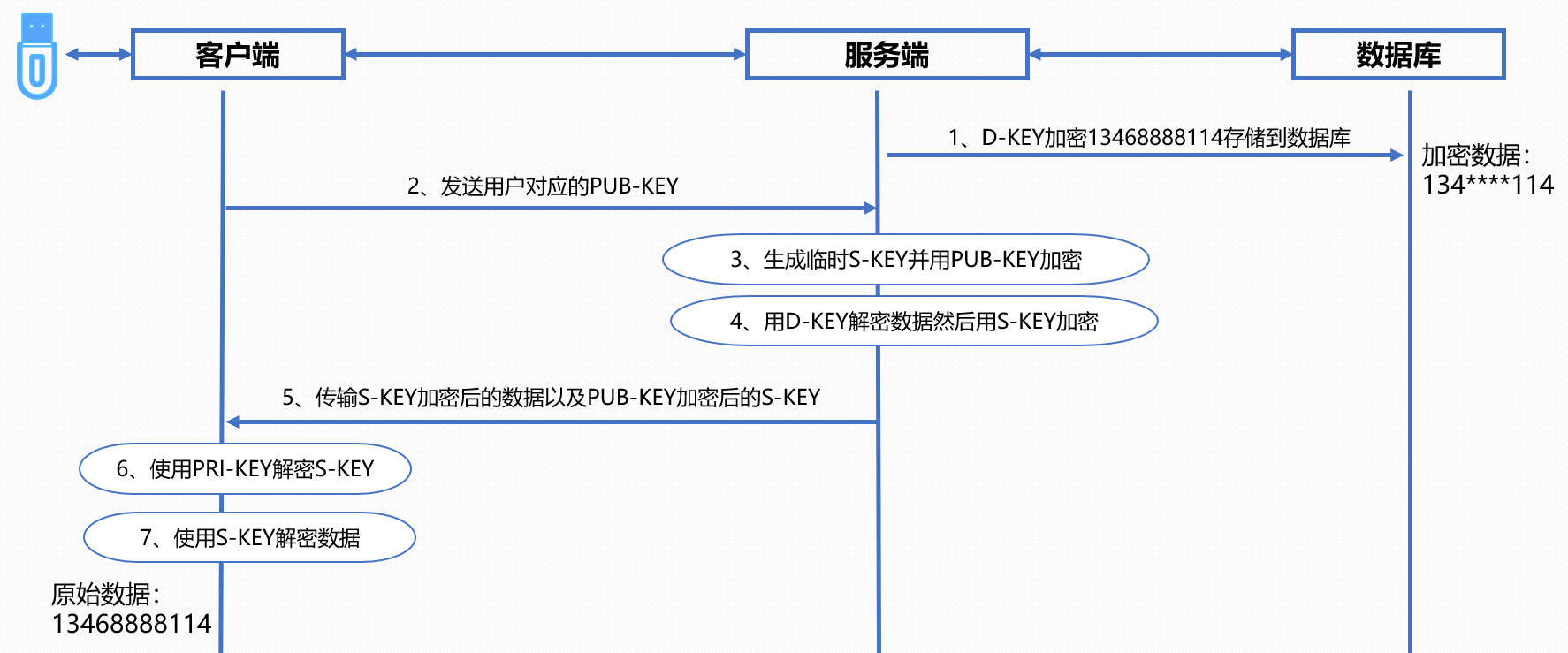
【安当产品应用案例100集】010-基于国密UKEY的信封加密应用案例
安当有个客户开发了一套C/S架构的软件,Server在云端,Client由不同的用户使用。最初软件设计开发的时候,没有考虑数据安全形势日渐严峻的问题,Server端和Client端直接就建立一个socket连接来进行通信,Server端发出去的数…...
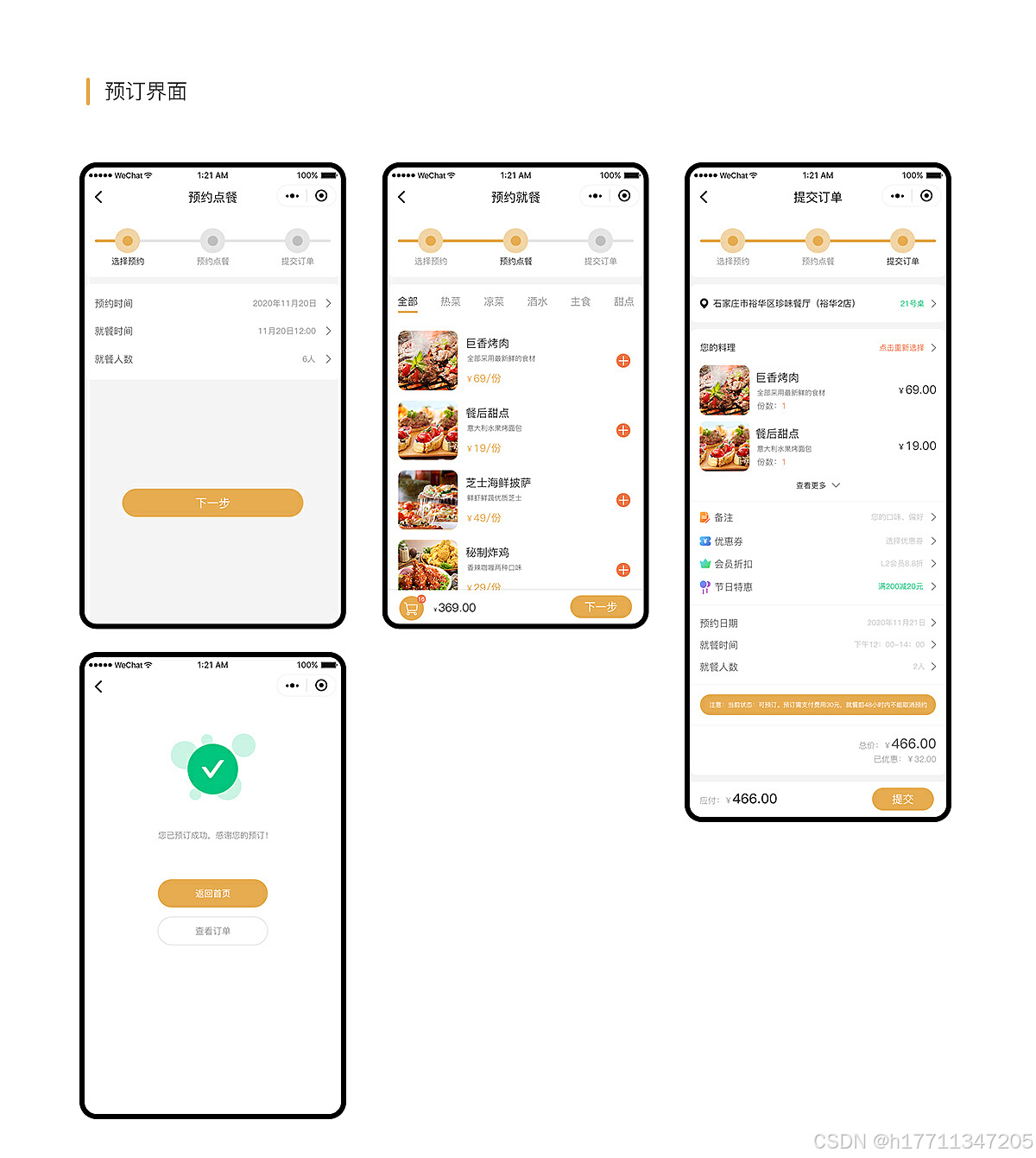
扫码点餐系统小程序功能分析
扫码点餐系统小程序通常具备以下核心功能: 用户界面:提供直观易用的界面,方便用户浏览菜单、选择菜品、查看订单状态等 。菜单展示:展示餐厅的菜单,包括菜品图片、价格、描述等信息 。扫码点餐:用户通过…...

网络安全——基础知识记忆梳理
1. SQL注入攻击 SQL注入攻击是一种常见的网络安全威胁,它利用Web应用程序中对用户输入的数据的不正确处理,攻击者可以在SQL查询中注入恶意代码,从而执行非授权的数据库操作。这种攻击方式可以导致数据泄漏、数据篡改、绕过认证等多种安全问题…...

GitHub开源的轻量级文件服务器,可docker一键部署
文件服务器 介绍安装使用命令使用API调用 介绍 项目github官网地址 Dufs是一款由Rust编写的轻量级文件服务器,不仅支持静态文件服务,还能轻松上传、下载、搜索文件,甚至支持WebDAV,让我们通过Web方式远程管理文件变得轻而易举。…...

Scratch编程深度探索:解锁递归与分治算法的奥秘
标题:Scratch编程深度探索:解锁递归与分治算法的奥秘 在编程的世界里,递归和分治算法以其精妙的逻辑结构和解决问题的能力而著称。Scratch,这款专为儿童和初学者设计的图形化编程工具,是否能够支持实现这样复杂的逻辑…...
使用docker compose一键部署 Portainer
使用docker compose一键部署 Portainer Portainer 是一款轻量级的应用,它提供了图形化界面,用于方便地管理Docker环境,包括单机环境和集群环境。 1、创建安装目录 mkdir /data/partainer/ -p && cd /data/partainer2、创建docker…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
