7. 数据结构—二叉树(链式存储)
1. 内容
包括链式存储二叉树的 递归与非递归实现的先序、中序以及后序遍历、层序遍历、创建二叉树、计算深度、总节点数。
2. 实现代码
注意:只是伪代码,如果想要运行的话在细节方面需要自己修正,栈和队列的方法实现需要引进或者使用其C++自带的功能函数。
#include<bits/stdc++.h>
using namespace std;typedef char ElemType;typedef struct BiTNode{ElemType data; //数据域 struct BiTNode *lchild,*rchild; //左右孩子指针
}BiTNode, *BiTree;//1. 先序遍历(根左右)->递归实现
void PreOrderTraverse(BiTree T){if(T){cout<<T->data;PreOrderTraverse(T->lchild);PreOrderTraverse(T->rchild);}
}// 先序遍历(根左右)-> 栈实现
void PreOrderTraverse(BiTree T){BiTree p=T; //指向当前访问数的位置InitStack(S); //存储根,便于回溯while(p||!StackEmpty(S)){if(p){cout<<p->data;Push(S,p);p=p->lchild;}else{ //需要将p指针进行回溯 Pop(S,p);p=p->rchild; } }
} //2.中序遍历(左根右)->递归实现
void InOrderTraverse(BiTree T){if(T){InOrderTraverse(T->lchild);cout<<T->data;InOrderTraverse(T->rchild);}
}//中序遍历(左根右)->栈实现
//思路:找到最左边的节点输出之后,通过栈找到最近的根,修改指针回溯
void InOrderTraverse(BiTree T){InitStack(S); //初始化栈S,用于记录最近的根,便于回溯BiTree p=T; //记录遍历位置while(p||!StackEmpty(S)){if(p){ //找到最左边的节点 Push(S,p);p=p->lchild;}else{ Pop(S,p);cout<<p->data; //输出最左边节点的值p=p->rchild; //实现回溯 }}
}//3.后序遍历(左右根)->递归实现
//使用栈实现和前面先中序逻辑差不多,但是必须得左子树和右子树访问完了之后才能访问根,更麻烦(有时间再写)
void PostOrderTraverse(BiTree T){if(T){PostOrderTraverse(T->lchild);PostOrderTraverse(T->rchild);cout<<T->data;}
}//4.层序遍历(使用队列)
void LevelOrderTraverse(BiTree T){BiTree p;InitQueue(Q);EnQueue(Q,T);while(!QueueEmpty(Q)){DeQueue(Q,p);cout<<p->data;if(p->lchild!=NULL)EnQueue(p->lchild);if(p->rchild!=NULL)EnQueue(p->rchild);}
}//5. 使用先序遍历创建二叉树(不存在左右子树需要输入#表示)
//其余遍历只需将位置改变一下即可,不再赘述
void CreateBiTree(BiTree &T){char ch;cin>>ch;if(ch=='#')T=NULL;else{T=new BiTNode;T->data=ch;CreateBiTree(T->lchild);CreateBiTree(T->rchild);}
} //6.计算二叉树的深度
//递归左子树和右子树的深度,选择最大的+1即可
int Depth(BiTree T){if(T==NULL) return 0;int m=Depth(T->lchild);int n=Depth(T->rchild);return max(m,n)+1;
} //7.统计二叉树节点的个数
int NodeCount(BiTree T){if(T==NULL) return 0;return NodeCount(T->lchild)+NodeCount(T->rchild)+1;
} 相关文章:
)
7. 数据结构—二叉树(链式存储)
1. 内容 包括链式存储二叉树的 递归与非递归实现的先序、中序以及后序遍历、层序遍历、创建二叉树、计算深度、总节点数。 2. 实现代码 注意:只是伪代码,如果想要运行的话在细节方面需要自己修正,栈和队列的方法实现需要引进或者使用其C自…...

AScript 的UI asui模板的导入
两种方案: 第一种直接在web端,右击UI文件夹 第二种在pycharm,也是右击UI文件夹 调用UI,在init类中直接调用即可...

Linux shell编程学习笔记75:sed命令——沧海横流任我行(下)
0 前言 在 Linux shell编程学习笔记73:sed命令——沧海横流任我行(上)-CSDN博客文章浏览阅读684次,点赞32次,收藏24次。在大数据时代,我们要面对大量数据,有时需要对数据进行替换、删除、新增、…...

探索Scratch中的物理世界:碰撞与重力的编程之旅
标题:探索Scratch中的物理世界:碰撞与重力的编程之旅 Scratch是一款由麻省理工学院媒体实验室开发的编程教育工具,它以图形化编程界面为特色,让初学者能够轻松地学习编程基础。Scratch不仅支持基本的编程逻辑,如循环、…...

大模型重塑就医体验:医联MedGPT助力健康中国建设
来源:新华网 2024 08/22 11:24:15 【责任编辑:吴起龙】 随着“百模大战”的加速推进,AI大模型的应用逐渐成为各行业关注的焦点。在这一背景下,医疗行业也迎来了AI技术的深度渗透。自2023年起,百度、科大讯飞、百川智能、商汤…...

TOMCAT全解
目录 一 、WEB技术简介 HTTP协议 B/S 结构 前端三大核心技术简介 HTML CSS JavaScript 二 、WEB框架 web资源和访问 后台应用架构 三、tomacat的介绍 四、tomcat的部署 tomcat的反向代理 tomcat的负载均衡 memcached的安装与启动 tomcat的session会话保持 一 、WE…...

UDP+TCP
一、UDP协议 1.recvfrom:recvform(int sockfd,void *buf,size_t len,int flags,struct sockaddr *src_addr,socklen_t *addrlen); 参数:socket的fd; 保存数据的空间地址 ; 空间大小; 默认接收方式(默认阻塞…...
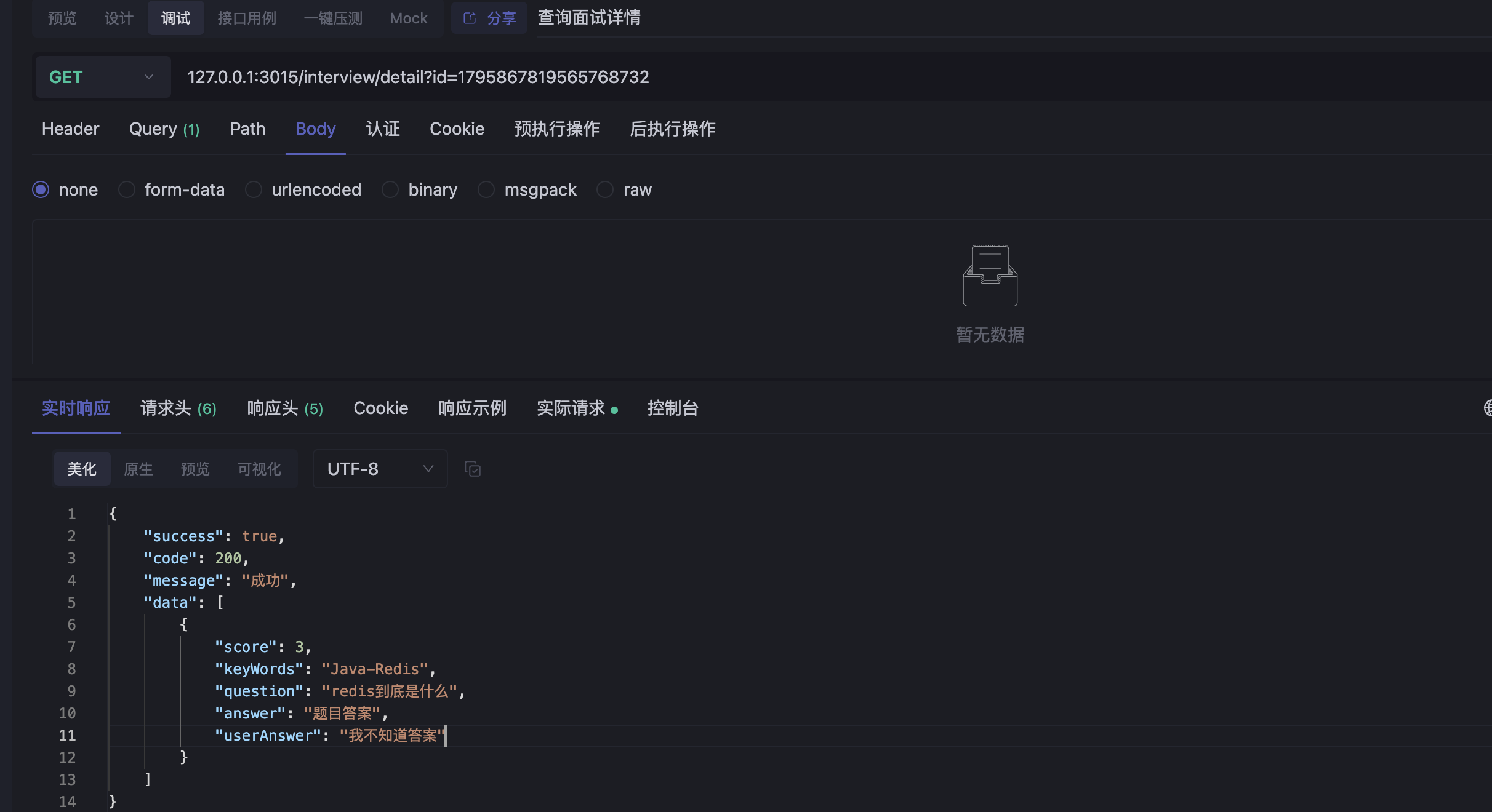
分页查询面试记录和面试详情
文章目录 1.分页查询面试记录1.req和vo1.InterviewHistoryReq.java2.InterviewHistoryVO.java 2.InterviewController.java3.service1.InterviewHistoryService.java2.InterviewHistoryServiceImpl.java 4.测试 2.查询面试详情1.InterviewQuestionHistoryVO.java2.InterviewCon…...

Oracle 同义词SYNONYM 的实战使用
Oracle中的同义词(SYNONYM)是一种数据库对象,它为其他数据库对象(如表、视图、序列、存储过程、函数等)提供了一个别名。这个别名可以在SQL语句中代替原始对象的名称,从而简化查询和引用,提高数…...

实验11-1-8 查找子串
本题要求实现一个字符串查找的简单函数。 函数接口定义: char *search( char *s, char *t );函数search在字符串s中查找子串t,返回子串t在s中的首地址。若未找到,则返回NULL。 输入样例1: The C Programming Language ram输出样…...

Git存储库添加空目录-添加占位文件
Git本身并不会跟踪和管理空目录,它只会记录和管理文件的变化。因此,在操作空目录时,我们需要借助一些技巧来实现我们的需求。通过添加一个空的.gitignore或.gitkeep文件或添加一个占位文件,我们可以欺骗Git,并使其将空…...

基于x86 平台opencv的图像采集和seetaface6的人脸识别功能
目录 一、概述二、环境要求2.1 硬件环境2.2 软件环境三、开发流程3.1 编写测试3.2 配置资源文件3.2 验证功能一、概述 本文档是针对x86 平台opencv的图像采集和seetaface6的人脸识别功能,opencv通过读取本地图像,将采集的本地图像送给seetaface6的人脸识别模块从而实现人脸识…...

Git 的基本使用
1.创建 Git 本地仓库 仓库是进⾏版本控制的⼀个⽂件⽬录。我们要想对⽂件进⾏版本控制,就必须先创建⼀个仓库出来,例如下面代码创建了gitcode_linux的文件夹,之后再对其进行初始化。创建⼀个 Git 本地仓库对应的命令为 git init ,…...

如何解决 Cloudflare | 使用 Puppeteer 和 Node.JS
我认为,现在自动化任务越多,越能体现它们的价值,因此挑战也变得更加明显和困难。例如,Cloudflare 目前提供了强有力的安全措施来保护网站免受所有形式的自动化工具的侵扰。 但对于从事自动化项目(如网络爬虫、数据提取…...

笔记redis
Redis 介绍 Redis(Remote Dictionary Server)是用C语言开发的一个基于内存的键值对数据库 所有数据都在内存中,访问速度非常快:读的速度是110000次/s,写的速度是81000次/s适合存储热点数据(商品、新闻资…...

Django 后端架构开发:手机与邮箱验证码接入、腾讯云短信SDK和网易邮箱
Django 后端架构开发:手机与邮箱验证码接入、腾讯云短信SDK和网易邮箱接入 🌟 手机短信与邮箱短信验证码的应用场景 在现代应用中,短信和邮箱验证码是用户验证和安全管理的关键组成部分。它们广泛应用于注册、登录、找回密码等场景…...

RAID 方案比较
RAID(Redundant Array of Independent Disks)技术用于将多个磁盘驱动器组合成一个逻辑单元,以提高性能、可靠性或两者兼顾。以下是常见 RAID 级别的比较: RAID 0(条带化) 磁盘数量:最少 2 块可…...
零成本搭建个人 APP 和小程序后台
前言 前面也说了,通过 GitHub PagesGitHub Actions 只是解决了动态数据展示,但是要零成本得完成将用户信息存储下来,并实现数据交互呢? 我开始是想用云文档,种种原因,我还是希望有个自己能二次修改的后台…...

LCP 633 平方数之和 [leetcode - 8]
最近是在研究双指针啊,leetcode刷的题都是这方面的。都记录在最近的文章里,大家有兴趣可以去我主页看看 LCP633 平方数之和 给定一个非负整数 c ,你要判断是否存在两个整数 a 和 b,使得 a2 b2 c 。 示例 1: 输入&…...

c语言试题及答案
1. 一个C程序的组成部分可以是( )。 A) 一个主函数和一至若干个其他函数 B) 一至若干个主函数 C) 一个主程序和一至若干个其他函数 D) 一个主程序和一至若干个子程序 2. 一个C程序的执行是从( )。 (A)本程序的main函数开始,到main函数结束 (B)本程序文件的第一个函…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

计算机系统结构复习-名词解释2
1.定向:在某条指令产生计算结果之前,其他指令并不真正立即需要该计算结果,如果能够将该计算结果从其产生的地方直接送到其他指令中需要它的地方,那么就可以避免停顿。 2.多级存储层次:由若干个采用不同实现技术的存储…...

数据库优化实战指南:提升性能的黄金法则
在现代软件系统中,数据库性能直接影响应用的响应速度和用户体验。面对数据量激增、访问压力增大,数据库性能瓶颈经常成为项目痛点。如何科学有效地优化数据库,提升查询效率和系统稳定性,是每位开发与运维人员必备的技能。 本文结…...
