LeetCode 算法:完全平方数 c++
- 原题链接🔗:完全平方数
- 难度:中等⭐️⭐️
题目
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
提示:
1 <= n <= 104
动态规划
动态规划(Dynamic Programming,简称DP)是一种在数学、管理科学、计算机科学、经济学和生物信息学等领域中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常用于优化问题,特别是那些具有重叠子问题和最优子结构性质的问题。
动态规划的关键概念:
- 重叠子问题:原问题可以分解为多个子问题,而这些子问题会重复出现多次。
- 最优子结构:一个问题的最优解包含其子问题的最优解。
- 无后效性:一旦某个状态被确定,它就不受之后决策的影响。
- 状态转移方程:描述了问题的状态如何从先前的状态转移而来。
动态规划的步骤:
- 定义状态:确定问题的状态,通常用数组或变量来表示。
- 确定状态转移方程:找出状态之间的关系,即如何从一个状态推导出另一个状态。
- 确定初始状态和边界条件:设置问题的起始状态和基本情况。
- 计算顺序:确定如何计算所有状态,通常从初始状态开始,逐步计算到最终状态。
- 构造最优解:从最终状态开始,逆向回溯到初始状态,构造问题的最优解。
动态规划的应用实例:
- 背包问题:给定一组物品和一个背包,确定在不超过背包容量的前提下,背包中物品的最优组合。
- 最长公共子序列:找出两个序列的最长公共子序列。
- 最短路径问题:在加权图中找到从起点到终点的最短路径。
- 矩阵链乘问题:计算矩阵序列的最优乘法顺序,以最小化总的标量乘法次数。
动态规划是一种强大的算法设计技术,适用于解决多种复杂问题,但需要仔细分析问题的结构,以确定是否可以应用动态规划方法。
题解
- 解题思路:
理解问题 给定一个正整数 n,目标是找到和为 n 的完全平方数的最少数量。完全平方数是指可以表示为某个整数的平方的数,例如 1, 4, 9, 16 等。
动态规划方法 这个问题可以通过动态规划(DP)来解决。我们定义一个数组 dp,其中 dp[i] 表示数字 i 可以由完全平方数相加得到的最少数量。
初始化 DP 数组 dp[0] 初始化为 0,因为和为 0 的最少数量是 0(不需要任何数)。 对于所有其他的 i,初始化 dp[i] 为一个非常大的数(例如 INT_MAX),表示暂时无法由完全平方数相加得到。
填充 DP 数组 对于每个 i 从 1 到 n,我们遍历所有可能的完全平方数 j * j(其中 j * j <= i),并更新 dp[i] 为 min(dp[i], dp[i - j*j] + 1)。这表示我们尝试用尽可能少的完全平方数来达到数字 i。
处理边界情况 确保处理所有可能的完全平方数,包括 1(因为 1 是最小的完全平方数,且经常出现在最优解中)。 考虑所有小于或等于 i 的完全平方数。
返回结果 最终,dp[n] 将包含和为 n 的完全平方数的最少数量
- c++ demo:
#include <iostream>
#include <vector>
#include <climits>
#include <cmath>// 动态规划求解和为n的完全平方数的最少数量
int numSquares(int n) {std::vector<int> dp(n + 1, INT_MAX);dp[0] = 0;for (int i = 1; i <= n; ++i) {int sqrt_val = static_cast<int>(std::sqrt(i));for (int j = 1; j <= sqrt_val; ++j) {dp[i] = std::min(dp[i], dp[i - j * j] + 1);}}return dp[n];
}// 主函数,用于测试
int main() {int n = 12; // 可以修改这个值来测试不同的输入std::cout << "The least number of perfect square numbers which sum to " << n << " is: " << numSquares(n) << std::endl;return 0;
}
- 输出结果:
The least number of perfect square numbers which sum to 12 is: 3
- 代码仓库:numSquares
相关文章:

LeetCode 算法:完全平方数 c++
原题链接🔗:完全平方数难度:中等⭐️⭐️ 题目 给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。 完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的…...

深入CSS 布局——WEB开发系列29
CSS 页面布局技术允许我们拾取网页中的元素,并且控制它们相对正常布局流、周边元素、父容器或者主视口/窗口的位置。 一、正常布局流(Normal Flow) CSS的布局基础是“正常流”,也就是页面元素在没有特别指定布局方式时的默认排列…...

视频的容器格式和编码格式详解
视频的容器格式和编码格式是视频文件的两个核心概念,它们相互关联但具有不同的功能。以下是详细的解释: 1. 容器格式 (Container Format) 容器格式,又称封装格式,指的是视频文件的外壳或容器,它用于封装视频、音频、…...
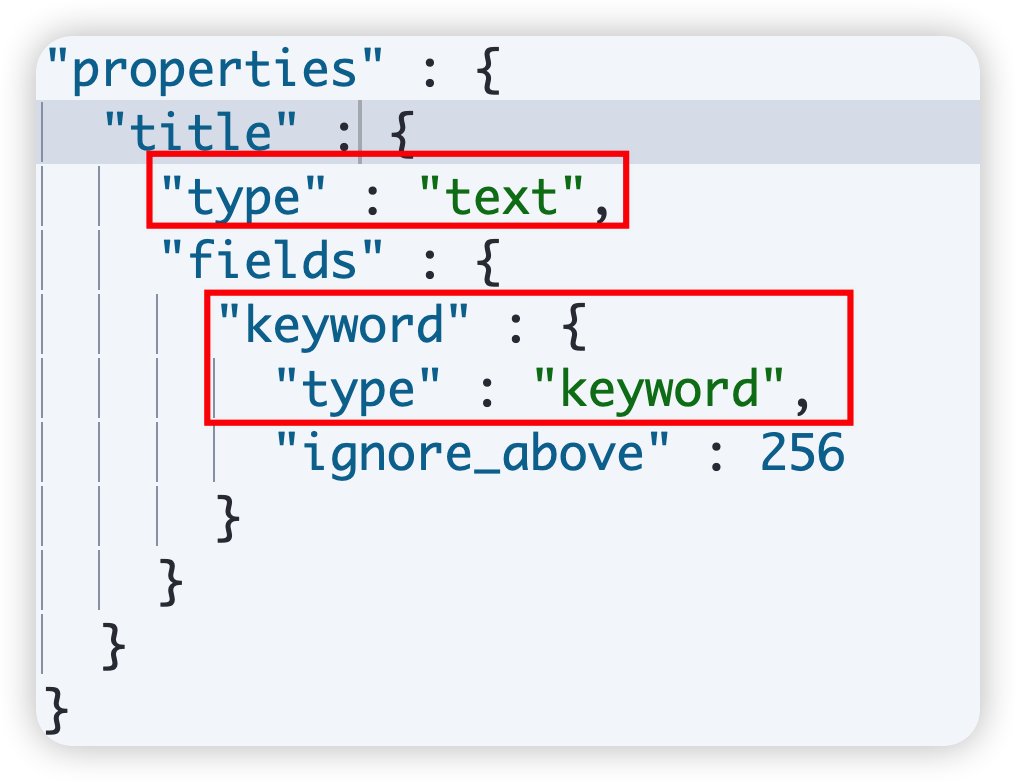
Elasticsearch Mapping 详解
1 概述 映射的基本概念 Mapping 也称之为映射,定义了 ES 的索引结构、字段类型、分词器等属性,是索引必不可少的组成部分。 ES 中的 mapping 有点类似与DB中“表结构”的概念,在 MySQL 中,表结构里包含了字段名称,字…...

WPF 利用视觉树获取指定名称对象、指定类型对象、以及判断是否有验证错误
1.利用视觉树获取指定名称对象 /// <summary> /// Finds a Child of a given item in the visual tree. /// </summary> /// <param name"parent">A direct parent of the queried item.</param> /// <typeparam name"T">T…...
`, `sub()`, `subn()`方法的作用)
了解`re`模块的`split()`, `sub()`, `subn()`方法的作用
在Python中,re模块(即正则表达式模块)提供了强大的字符串处理能力,允许你通过模式匹配来执行复杂的文本搜索、替换和分割等操作。其中,split(), sub(), 和 subn() 方法是re模块中非常实用的几个函数,它们各…...

机器学习交通流量预测实现方案
机器学习交通流量预测实现方案 实现方案 1. 数据预处理 2. 模型选择 3. 模型训练与评估 代码实现 代码解释 小结 🎈边走、边悟🎈迟早会好 交通流量预测是机器学习在智能交通系统中的典型应用,通常用于预测道路上的车辆流量、速度和拥…...

QNN:基于QNN+example重构之后的yolov8det部署
QNN是高通发布的神经网络推理引擎,是SNPE的升级版,其主要功能是: 完成从Pytorch/TensorFlow/Keras/Onnx等神经网络框架到高通计算平台的模型转换; 完成模型的低比特量化(int8),使其能够运行在高…...

Redis实战宝典:开发规范与最佳实践
目录标题 Key命名设计:可读性、可管理性、简介性Value设计:拒绝大key控制Key的生命周期:设定过期时间时间复杂度为O(n)的命令需要注意N的数量禁用命令:KEYS、FLUSHDB、FLUSHALL等不推荐使用事务删除大key设置合理的内存淘汰策略使…...

RPC的实现原理架构
RPC(Remote Procedure Call,远程过程调用)是一种允许程序调用位于不同地址空间或网络上的函数或方法的技术,尽管这些调用看起来像是本地调用。RPC 的实现极大地简化了分布式系统中的通信,避免了开发人员直接处理底层网…...

OpenXR Monado Hello_xr提交Frame
OpenXR Monado Hello_xr提交Frame @src/tests/hello_xr/openxr_program.cpp RenderFrame())xrWaitFrame(m_session, &frameWaitInfo, &frameState)xrBeginFrame(m_session, &frameBeginInfo)std::vector<XrCompositionLayerBaseHeader*> layers;std::vecto…...

huggingface快速下载模型及其配置
大家知道,每次进huggingface里面一个个手动下载文件然后再上传到我们的服务器是很麻烦的。其实huggingface提供了下载整个包的命令,很简单,如下: 1. 进入huggingface官网,随便搜索一个模型,点击右上角的三…...

虚幻5|不同骨骼受到不同伤害|小知识(2)
1.蓝图创建一个结构,B_BoneDamage 结构里添加一个浮点变量,表示伤害倍数 2.当我们创建了一个结构,就需要创建一个数据表格,数据表格可以选择对应的结构 不同骨骼不同倍数伤害,骨骼要对应骨骼网格体的名称 3.把我们br…...

达梦SQL 优化简介
目录 一、定位慢 SQL (一)开启跟踪日志记录 1.跟踪日志记录配置 (二)通过系统视图查看 1.SQL 记录配置 2.查询方式 二、SQL分析方法 (一)执行计划 1.概述 2.查看执行计划 (二&#x…...

题解:CF1070B Berkomnadzor
CF1070B Berkomnadzor 题解 解题思路 不难想到将 IP 地址转化为二进制后插入一个字典树中,转化后二进制的长度就是 x x x 的长度。我们需要记录每个串结尾的颜色,不妨设黑名单为 1 1 1,白名单为 0 0 0,初始时每个位置的颜色是…...

shell 学习笔记:数组
目录 1. 定义数组 2. 读取数组元素值 3. 关联数组 4. 在数组前加一个感叹号 ! 可以获取数组的所有键 5. 在数组前加一个井号 # 获取数组的长度 6. 数组初始化的时候,也可以用变量 7. 循环输出数组的方法 7.1 for循环输出 7.2 while循环输出 7.2.1 …...

计算机基础知识复习9.5
数据交换 电路交换:交换信息的两个主机之间简历专用通道,传输时延小,实时性强,效率低,无法纠正错误。 报文交换:信息拆分成小包(报文)大小无限制,有目的/源等信息提高利用率。有转…...

spark.sql
from pyspark.sql import SparkSession from pyspark.sql.functions import col, count, mean, rank, row_number, desc from pyspark.sql.window import Window from pyspark.sql.types import StructType, StructField, StringType, IntegerType# 初始化 SparkSession 对象 s…...

2024 数学建模高教社杯 国赛(A题)| “板凳龙”舞龙队 | 建模秘籍文章代码思路大全
铛铛!小秘籍来咯! 小秘籍团队独辟蹊径,运用等距螺线,多目标规划等强大工具,构建了这一题的详细解答哦! 为大家量身打造创新解决方案。小秘籍团队,始终引领着建模问题求解的风潮。 抓紧小秘籍&am…...

kaggle注册收不到验证码、插件如何下载安装
综合这三个来看, 1.插件下载用的大佬给的分享链接 2.下载好压缩包以后需要解压缩 Header Editor插件网盘下载安装教程 - 哔哩哔哩 (bilibili.com) 3.安装插件时没找到crx文件,在浏览器插件界面点击“加载解压缩的扩展” 4.复制网址到插件里ÿ…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
