[详细建模已更新]2024数学建模国赛高教社杯A题:“板凳龙” 闹元宵 思路代码文章助攻手把手保姆级
A 题 “板凳龙” 闹元宵
“板凳龙”,又称“盘龙”,是浙闽地区的传统地方民俗文化活动。人们将少则几十条,多则上百条的板凳首尾相连,形成蜿蜒曲折的板凳龙。盘龙时,龙头在前领头,龙身和龙尾相随盘旋,整体呈圆盘状。一般来说,在舞龙队能够自如地盘入和盘出的前提下,盘龙所需要的面积越小、行进速度越快,则观赏性越好。
某板凳龙由 223 节板凳组成,其中第 1 节为龙头,后面 221 节为龙身,最后 1 节为龙尾。龙头的板长为 341 cm,龙身和龙尾的板长均为 220 cm,所有板凳的板宽均为 30 cm。每节板凳上均有两个孔,孔径(孔的直径)为 5.5 cm,孔的中心距离最近的板头 27.5 cm(见图 1 和图 2)。相邻两条板凳通过把手连接(见图 3)。
图 1 龙头的俯视图
图 2 龙身和龙尾的俯视图
图 3 板凳的正视图
请建立数学模型,解决以下问题:
问题一:舞龙队沿螺距为55 cm的等距螺线顺时针盘入的建模分析
1. 问题背景
“板凳龙”是由223节板凳组成的舞龙队,其中:
- 第1节为龙头,板长为341 cm;
- 第2节到第221节为龙身,板长为220 cm;
- 第222节为龙尾,板长为220 cm;
- 所有板凳的宽度均为30 cm。
板凳之间通过把手连接,初始时刻龙头前把手的行进速度为1 m/s,且位于螺线的第16圈A点,沿着螺旋线进行顺时针的盘入运动。
2. 问题要求
从初始时刻到300秒,要求每秒计算整个舞龙队的各个节点的位置和速度,包括:
- 龙头前把手
- 龙身第1、51、101、151、201节的前把手
- 龙尾后把手
此外,还需要在特定时刻(如0 s, 60 s, 120 s等)给出上述节点的位置和速度,并将结果保存到 result1.xlsx 文件中。
3. 螺旋线模型
舞龙队沿着等距螺线行进。等距螺线的极坐标方程为:
[
r(\theta) = a + b\theta
]
其中,螺距 ( p = 55 ) cm,因此螺线的参数 ( b ) 可以表示为:
[
b = \frac{p}{2\pi} = \frac{55}{2\pi} \approx 8.75 , \text{cm}
]
设 ( \theta ) 为极角,则螺线在极坐标系中的坐标为:
[
x(\theta) = r(\theta) \cdot \cos(\theta)
]
[
y(\theta) = r(\theta) \cdot \sin(\theta)
]
龙头前把手的初始位置对应于螺线的第16圈,即初始角度为 ( \theta_0 = 16 \times 2\pi = 32\pi )。
4. 龙头速度与时间关系
由于龙头前把手的速度恒定为1 m/s,因此可以通过如下关系推导出每一时刻的角度变化:
[
v = \frac{ds}{dt} = 1 , \text{m/s}
]
其中,( s ) 为龙头前把手沿螺线的弧长,弧长可以通过积分表示为:
[
s = \int_0^{\theta} \sqrt{r^2(\theta) + \left(\frac{dr}{d\theta}\right)^2} , d\theta
]
每一秒的时间步长对应的角度增量 ( \Delta \theta ) 可以通过数值方法计算,结合螺线方程更新龙头的位置。
5. 龙身及龙尾的运动
龙身和龙尾的每一节板凳均由前节板凳带动。对于每一节板凳的运动,需要考虑以下几何约束:
- 相邻板凳的距离为220 cm;
- 每节板凳的把手位于螺线上,保持连接关系。
龙身的运动可以通过相邻板凳的相对位置变化推导出其每一时刻的位置和速度。由于龙头的速度恒定为1 m/s,因此龙身后部的速度会有微小的变化,特别是在螺线盘入时。
6. 数值计算
为了得到每秒的节点位置和速度,我们可以使用数值积分方法(如欧拉法或龙格库塔法)来模拟整个舞龙队的运动。每一个时间步长 ( \Delta t = 1 , \text{s} ),通过以下步骤计算:
- 计算龙头的角度增量 ( \Delta \theta );
- 更新龙头的极坐标位置 ( (r(\theta), \theta) );
- 通过几何约束,依次计算龙身和龙尾的每节板凳的位移和速度;
- 将每秒的结果保存至
result1.xlsx文件中。
7. 特定时刻的位置和速度
根据题目要求,分别在 0 s, 60 s, 120 s, 180 s, 240 s, 300 s 时,给出以下节点的位置信息和速度:
- 龙头前把手 ( x_{\text{龙头}}(t), y_{\text{龙头}}(t) )
- 第1节龙身前把手 ( x_{\text{第1节}}(t), y_{\text{第1节}}(t) )
- 第51节龙身前把手 ( x_{\text{第51节}}(t), y_{\text{第51节}}(t) )
- 第101节龙身前把手 ( x_{\text{第101节}}(t), y_{\text{第101节}}(t) )
- 第151节龙身前把手 ( x_{\text{第151节}}(t), y_{\text{第151节}}(t) )
- 第201节龙身前把手 ( x_{\text{第201节}}(t), y_{\text{第201节}}(t) )
- 龙尾后把手 ( x_{\text{龙尾}}(t), y_{\text{龙尾}}(t) )
速度的计算采用位移除以时间步长:
[
v = \frac{\Delta s}{\Delta t}
]
每节板凳的速度也需要记录并输出。
8. 总结
本问题的核心在于通过螺旋线的几何模型和舞龙队的运动学模型,推导出每一节板凳
问题二:确定舞龙队盘入的终止时刻,避免板凳之间碰撞
1. 问题描述
舞龙队按照问题一设定的螺旋线盘入。随着时间的推移,龙头不断在螺旋线上前进,后面的龙身和龙尾会逐渐跟随并紧密排列。当螺线的半径变得越来越小,板凳之间的距离可能会缩短到发生碰撞的程度。
问题二要求我们确定舞龙队盘入的终止时刻,即当板凳之间不能继续盘入而发生碰撞时的时刻。并在该时刻输出舞龙队的位置信息和速度。
2. 问题要求
- 确定板凳之间最小的安全距离,避免相邻板凳发生物理碰撞;
- 计算舞龙队不能继续盘入的终止时刻;
- 输出此时舞龙队的位置信息和速度,并将结果保存到
result2.xlsx文件中; - 额外要求给出终止时刻龙头、龙身第1、51、101、151、201节龙身前把手及龙尾后把手的位置和速度。
3. 碰撞条件的分析
在舞龙队盘入过程中,相邻板凳保持通过把手相连,但随着螺线半径的逐渐减小,板凳之间的相对距离会变短。我们需要定义一个最小安全距离,以确保舞龙队不会发生碰撞。
假设两个相邻板凳之间的最小安全距离为220 cm,即板凳的长度。具体来说,如果两节相邻板凳在螺线上相距小于这个距离,则认为发生碰撞,不能继续盘入。因此,终止时刻可以通过如下条件来确定:
相关文章:

[详细建模已更新]2024数学建模国赛高教社杯A题:“板凳龙” 闹元宵 思路代码文章助攻手把手保姆级
A 题 “板凳龙” 闹元宵 “板凳龙”,又称“盘龙”,是浙闽地区的传统地方民俗文化活动。人们将少则几十条,多则上百条的板凳首尾相连,形成蜿蜒曲折的板凳龙。盘龙时,龙头在前领头,龙身和龙尾相随盘旋&#x…...

网络编程(TCP+网络模型)
【1】TCP 初版服务器 #include <stdio.h> #include <sys/types.h> /* See NOTES */ #include <sys/socket.h> #include <netinet/in.h> #include <netinet/ip.h> #include <unistd.h> #include <arpa/inet.h> #include <string.h…...

Docker Image 命令
文章目录 目录 文章目录 1 . Docker镜像是什么? 2 . 镜像命令详解 docker images docker tag docker pull docker rmi docker save 总结 1 . Docker镜像是什么? Docker image 本质上是一个 read-only 只读文件, 这个文件包含了文件系统、 源码、库文件…...

如何在IntelliJ IDEA中将Tab设置为4个空格
前言 IntelliJ IDEA是一个强大的开发工具,支持多种编程语言。为了保持代码整洁一致,开发者经常需要调整编辑器中的Tab和缩进设置。 步骤1: 打开设置 首先,启动IntelliJ IDEA。在主界面上方的菜单栏中找到 File(文件)…...

ASP.NET Core 入门教学十五 异步编程
在ASP.NET Core中,异步编程是一种非常重要的技术,它可以提高应用程序的性能和响应能力。本教程将介绍如何在ASP.NET Core中使用异步编程。 1. 异步编程基础 异步编程允许程序在等待某些操作(如I/O操作)完成时继续执行其他任务&a…...

pycharm 2024.1下载、安装
下载 下载官网: Other Versions - PyCharm 选择需要的版本下载,这里以 2024.1 的版本为例 安装 双击下载好的安装程序,点击下一步 选择安装路径,最好是英文路径;然后下一步 点击完成 激活 网址: Some…...

实变函数精解【18】
文章目录 有限测度有限测度概率测度有限测度与概率测度的关系 σ \sigma σ-有限测度计数测度完备概率测度 参考文献 有限测度 首先,我们来明确“测度”的概念。在数学中,测度是一个将集合映射到非负实数(通常是实数的扩展,包括正…...

【深入解析】AI工作流中的HTTP组件:客户端与服务端执行的区别
在当今快速发展的技术环境中,AI工作流的设计和实现变得愈发重要。尤其是在处理HTTP组件时,前端执行与后端执行之间的区别,往往会对系统的安全性和数据的准确性产生深远的影响。今天,我们就来深入探讨这一话题,揭示前端…...

用亚马逊云科技Graviton高性能/低耗能处理器构建AI向量数据库(上篇)
简介: 今天小李哥将介绍亚马逊推出的云平台4代高性能计算处理器Gravition,并利用该处理器构建生成式AI向量数据库。利用向量数据库,我们可以开发和构建多样化的生成式AI应用,如RAG知识库,特定领域知识的聊天机器人等。…...

调用火山云的语音生成TTS和语音识别STT
首先需要去火山云的控制台开通TTS和STT服务语音技术 (volcengine.com) 火山这里都提供了免费的额度可以使用 我这里是使用了java来调用API 目前我还了解到阿里的开源项目SenseVoice(STT)和CosyVoice(TTS)非常的不错,但是都是使用Python开发…...

中间件解析漏洞
一:IIS less-1 IIS6.X 步骤一:在iis的⽹站根⽬录新建⼀个名为x.asp的⽂件 步骤二:在x.asp中新建⼀个.txt⽂件,内容为<%now()%> asp代码,更改后缀为jpg 步骤三:在外部浏览器进行访问Window2003的ip/x.asp/1.jpg࿰…...

如何在Mac电脑上本地部署Stable Diffusion:详细教程(webUI)
Stable Diffusion是一款强大的AI生成图像模型,它可以基于文本描述生成高质量的图像。对于想要在本地运行此模型的用户来说,使用Mac电脑部署Stable Diffusion是一个非常吸引人的选择,特别是对于M1或M2芯片的用户。本文将详细介绍如何在Mac上本…...

FPGA随记——移位寄存器
数电知识——移位寄存器:移位寄存器——数电第六章学习-CSDN博客 移位寄存器在FPGA中:FPGA原理与结构(5)——移位寄存器(Shift Registers)-CSDN博客...

Java | Leetcode Java题解之第390题消除游戏
题目: 题解: class Solution {public int lastRemaining(int n) {int a1 1;int k 0, cnt n, step 1;while (cnt > 1) {if (k % 2 0) { // 正向a1 a1 step;} else { // 反向a1 (cnt % 2 0) ? a1 : a1 step;}k;cnt cnt >> 1;step s…...

新型PyPI攻击技术可能导致超2.2万软件包被劫持
一种针对 Python 软件包索引(PyPI)注册表的新型供应链攻击技术已在野外被利用,并且目前正试图渗透到下游组织中。 软件供应链安全公司 JFrog 将其代号定为Revival Hijack,并称这种攻击方法可用于劫持 2.2万个现有 PyPI 软件包&am…...

spring cloud gateway 之删除请求头
在使用spring gateway作为网关时,我们经常需要在将请求转发到下游服务时,过滤掉某些请求头,以避免不必要的信息泄露,而spring gateway提供了RemoveRequestHeader内置的过滤器帮我们实现该功能,此外,我们也可…...

Flutter自动打包ios ipa并且上传
该脚本会自动打包iios ipa 并自动上传,中间自动flutter clean ,自动 pod install 里面需要填写自己应用的 apiKey和apiIssuer 如我的例子中apiKey 为 1234 apiIssuer 为5678, 首先flutter 工程目录 新建 shell目录,目录下新建ipa.sh文件&…...

深入理解synchronized的原理是什么
对象头锁机制原则 Synchronized 的原理是什么 Synchronized 是由JVM实现的一种实现互斥同步的实现方式。如果查看synchronized关键字修饰的字节码,会发现在编译器生成了monitorenter和monitorexit两个字节码指令。 这两个指令的意思就是在虚拟机执行到monitore…...

Electron32-Vue3OS桌面管理os模板|vite5+electron32+arco后台os系统
原创新作electron32.xvue3arco.design仿ipad/windows桌面os系统。 基于最新跨平台技术Electron32、Vite5、Vue3 setup、Pinia2、Arco-Design、Echarts、Sortablejs实战开发桌面版osx管理系统。内置ipad/windows两种桌面风格模板、动态json配置桌面图标、自研栅格拖拽布局模板。…...

c++ 定义函数
在C中,定义函数是一个基本的编程概念。函数是执行特定任务的一段代码,可以接受参数并返回值。下面是关于如何定义和使用函数的详细介绍。 1. 函数的基本结构 函数的基本结构包括以下几个部分: 返回类型:表示函数返回值的类型。…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

AT模式下的全局锁冲突如何解决?
一、全局锁冲突解决方案 1. 业务层重试机制(推荐方案) Service public class OrderService {GlobalTransactionalRetryable(maxAttempts 3, backoff Backoff(delay 100))public void createOrder(OrderDTO order) {// 库存扣减(自动加全…...
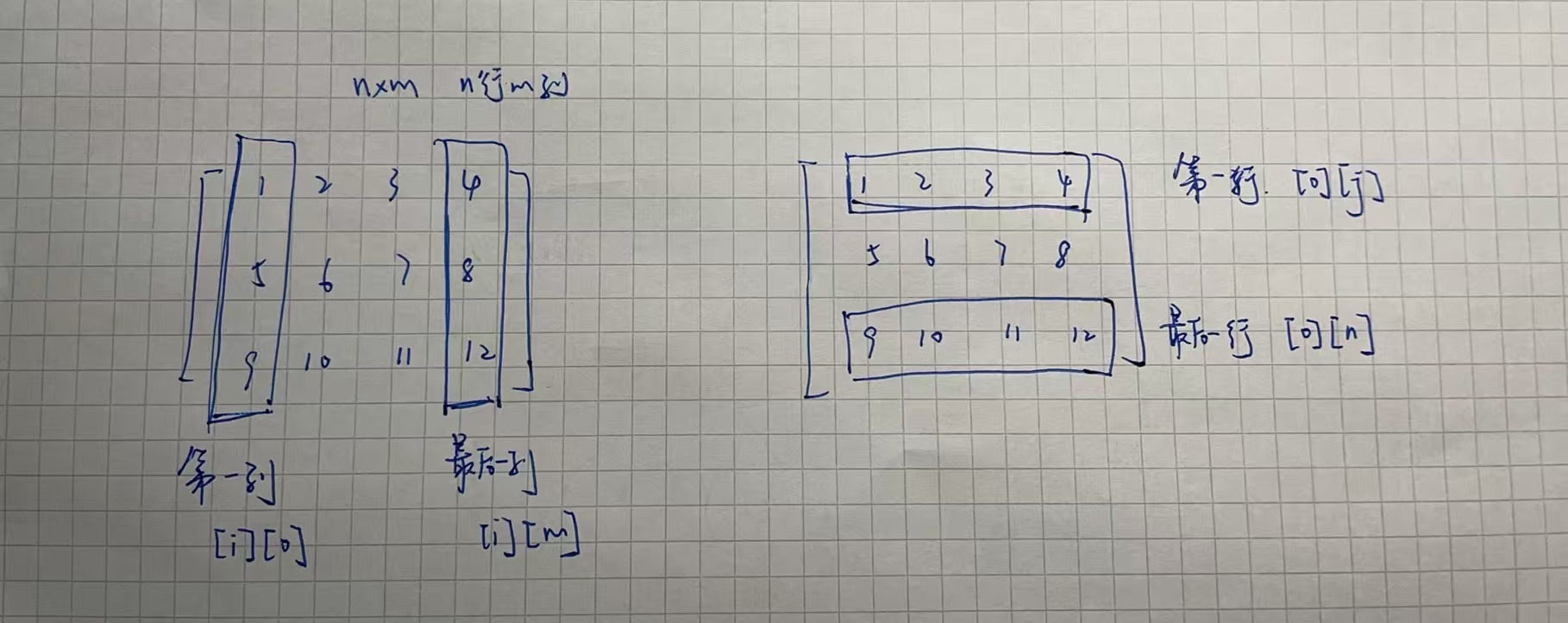
二维数组 行列混淆区分 js
二维数组定义 行 row:是“横着的一整行” 列 column:是“竖着的一整列” 在 JavaScript 里访问二维数组 grid[i][j] 表示 第i行第j列的元素 let grid [[1, 2, 3], // 第0行[4, 5, 6], // 第1行[7, 8, 9] // 第2行 ];// grid[i][j] 表示 第i行第j列的…...

Python爬虫(52)Scrapy-Redis分布式爬虫架构实战:IP代理池深度集成与跨地域数据采集
目录 一、引言:当爬虫遭遇"地域封锁"二、背景解析:分布式爬虫的两大技术挑战1. 传统Scrapy架构的局限性2. 地域限制的三种典型表现 三、架构设计:Scrapy-Redis 代理池的协同机制1. 分布式架构拓扑图2. 核心组件协同流程 四、技术实…...
