Javascript 使用中点查找矩形的角(Find Corners of Rectangle using mid points)
考虑一个矩形 ABCD,我们给出了边 AD 和 BC 中点(分别为 p 和 q)的坐标以及它们的长度 L(AD = BC = L)。现在给定参数,我们需要打印 4 个点 A、B、C 和 D 的坐标。

例子:
输入:p = (1, 0)
q = (1, 2)
L = 2
输出:(0,0),(0,2),(2,2),(2,0)
解释:
打印的点形成一个矩形,
满足输入约束。
输入:p = (1, 1)
q = (-1, -1)
L = 2*sqrt(2)
输出:(0,2),(-2,0),(0,-2),(2,0)
从问题陈述中可能出现 3 种情况:
矩形是水平的,即 AD 和 BC 平行于 X 轴
矩形是垂直的,即 AD 和 BC 平行于 Y 轴
矩形与轴线呈一定角度倾斜
前两种情况很简单,使用基本几何学就可以轻松解决。对于第三种情况,我们需要应用一些数学概念来找到点。
为了清楚起见,请考虑上图。我们有 p 和 q 的坐标。因此,我们可以找到 AD 和 BC 的斜率(因为 pq 垂直于 AD)。一旦我们有了 AD 的斜率,我们就可以找到通过 AD 的直线方程。现在我们可以应用距离公式来获得沿 X 轴和 Y 轴的位移。
如果 AD 的斜率 = m,则 m = (px- qx)/(qy- py)
以及沿 X 轴的位移,dx = L/(2*sqrt(1+m*m))
类似地,dy = m*L/(2*sqrt(1+m*m))
现在,我们可以通过简单地加减相应获得的位移来找到 4 个角的坐标。
下面是实现过程:
// Javascript program to find corner points of
// a rectangle using given length and middle
// points.
// Structure to represent a co-ordinate point
class Point
{
constructor(a,b)
{
this.x=a;
this.y=b;
}
}
// This function receives two points and length
// of the side of rectangle and prints the 4
// corner points of the rectangle
function printCorners(p,q,l)
{
let a = new Point(), b = new Point(),
c = new Point(), d = new Point();
// horizontal rectangle
if (p.x == q.x)
{
a.x = (p.x - (l / 2.0));
a.y = p.y;
d.x = (p.x + (l / 2.0));
d.y = p.y;
b.x = (q.x - (l / 2.0));
b.y = q.y;
c.x = (q.x + (l / 2.0));
c.y = q.y;
}
// vertical rectangle
else if (p.y == q.y)
{
a.y = (p.y - (l / 2.0));
a.x = p.x;
d.y = (p.y + (l / 2.0));
d.x = p.x;
b.y = (q.y - (l / 2.0));
b.x = q.x;
c.y = (q.y + (l / 2.0));
c.x = q.x;
}
// slanted rectangle
else
{
// calculate slope of the side
let m = (p.x - q.x) / (q.y - p.y);
// calculate displacements along axes
let dx = ((l / Math.sqrt(1 + (m * m))) * 0.5);
let dy = m * dx;
a.x = p.x - dx;
a.y = p.y - dy;
d.x = p.x + dx;
d.y = p.y + dy;
b.x = q.x - dx;
b.y = q.y - dy;
c.x = q.x + dx;
c.y = q.y + dy;
}
document.write(a.x + ", " + a.y + " <br>"
+ b.x + ", " + b.y + "<br>"
+ c.x + ", " + c.y + " <br>"
+ d.x + ", " + d.y + "<br>");
}
// Driver code
let p1 = new Point(1, 0), q1 = new Point(1, 2);
printCorners(p1, q1, 2);
let p = new Point(1, 1), q = new Point(-1, -1);
printCorners(p, q, (2 * Math.sqrt(2)));
// This code is contributed by rag2127
输出:
0,0
0、2
2,2
2,0
0、2
-2,0
0、-2
2,0
时间复杂度: O(1)
辅助空间: O(1)
相关文章:

Javascript 使用中点查找矩形的角(Find Corners of Rectangle using mid points)
考虑一个矩形 ABCD,我们给出了边 AD 和 BC 中点(分别为 p 和 q)的坐标以及它们的长度 L(AD BC L)。现在给定参数,我们需要打印 4 个点 A、B、C 和 D 的坐标。 例子: 输入:p (1,…...

【困难】 猿人学web第一届 第18题 jsvmp 洞察先机
文章目录 数据接口分析还原加密参数插桩调试分析日志插桩补充 python 代码 数据接口分析 数据接口 https://match.yuanrenxue.cn/match/18data 请求参数 {page: 页码, t: 时间戳, v: 加密值} 请求第一页不需要携带 t, v 参数 cookie 只需要携带 sessionid 只要 还原加密字段…...

IDEA Maven 源修改为国内阿里云镜像的正确方式
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storm…...

OpenCV 旋转矩形边界
边界矩形是用最小面积绘制的,所以它也考虑了旋转。使用的函数是**cv.minAreaRect**()。 import cv2 import numpy as npimgcv2.imread(rD:\PythonProject\thunder.jpg) img1cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) print(img.dtype) ret,threshcv2.threshold(img1,1…...
人车防撞系统安全生产方案
根据《市场监管总局关于2021~2023年全国特种设备安全状况的通告》数据显示:2023年:全国共发生特种设备事故和相关事故71起,其中死亡69人。包含叉车在内的场(厂)内专用机动车辆事故29起、死亡28人,占事故总数的40.85%、死亡人数的4…...

开放式耳机哪个牌子好?长文传授6招秘籍,彻底远离坑货!
大家好,作为一位专注于评测各类数码产品的博主,今天我特别推荐开放式耳机作为我们日常的首选。这种耳机以其独特的设计,避免了传统耳机长时间佩戴可能带来的不适和感染风险。开放式耳机佩戴简便且稳固,尤其适合热爱跑步和运动的…...

vue2和vue3双向绑定的原理
Vue.js 的双向绑定是 Vue 框架的核心特性之一,它允许数据和视图之间保持同步。虽然 Vue 2 和 Vue 3 都实现了双向绑定,但它们在实现细节上有所不同。 Vue 2 双向绑定的原理 在 Vue 2 中,双向绑定主要依赖于 Object.defineProperty 和观察者…...
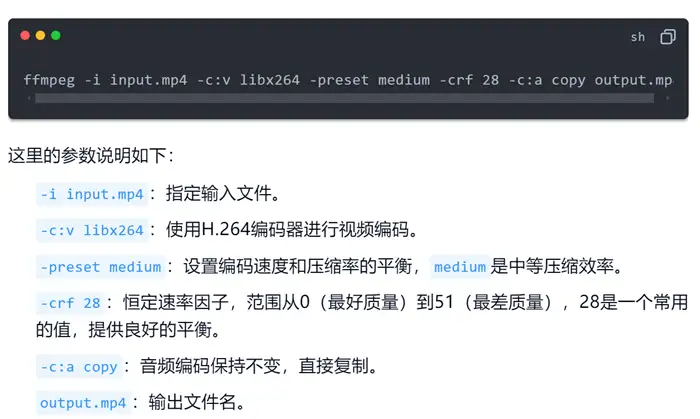
别为大文件烦恼!mp4文件太大怎么变小?3个管用方法
你是否曾经遇到过mp4视频文件过大的困扰?每当想要分享或存储mp4文件时,巨大的文件就成了阻碍。明明感觉感觉没占用多少空间,但是设备却常常出现空间过满警告。 没多少空间的设备真是让人大为恼火,没人想多花一份钱买设备。那么只…...

cocotb的接收和发送逻辑,还是没有弄明白
发送有两种方式 1、定义这样的发 通过前缀连接DUT里面的信号 发送的时候,通过.去访问就可以 2、如果是AXI总线,可以直接调用cocotb的库文件 AXIS总线可以包含以下的信号 通过这个类,可以产生一个AXIS的一帧数据 类的实现大概如下 然后也…...

XXL-JOB调度中心与执行器
XXL-JOB是一个轻量级的分布式任务调度平台,主要由调度中心和执行器两部分组成。下面详细讲解调度中心与执行器的功能和作用。 调度中心 调度中心是XXL-JOB的核心组件,负责任务的调度管理。其主要功能包括: 任务管理:调度中心提供…...
 绿色版)
Notepad++ 8.6.9 (代码编辑) 绿色版
Notepad编辑器是一款非常流行的编辑软件,对于技术白菜来说,有这么个神器真是方便多了,Notepad界面简洁明了,而且可以定制界面,又支持多国语言,是站长们的得力助手。免费、开源、绿色,对中文支持…...

【例003】利用MATLAB绘制有趣平面图形
题目: 用 ezplot 画出由方程 sin ( x 2 m y 2 1000 ) cos ( x y ) \sin(x^2\frac{my^2}{1000})\cos(xy) sin(x21000my2)cos(xy) 确定隐函数的图形。 求解: 我们分别取m为100,1000,10000不同的值,绘制不同情况下的图…...

Ignis公链探索生态建设新范式:产业区块链与GameFi双轨驱动
Ignis公链凭借其独特的技术架构,选择了产业区块链与GameFi这两个赛道作为生态建设的双轮驱动,逐步形成了一个多元化的Web3生态系统。 一、产业区块链的革新:Vessel Chain的成功案例 在产业区块链领域,Ignis公链通过推出Vessel Ch…...

河南测绘资质申请中的技术装备需求
技术装备要求概览 购置与测绘业务相适应的技术设备:需要购置与测绘业务相适应的技术设备,如全站仪、水准仪、GNSS接收机等。 需要建立技术装备清单,并确保这些设备处于良好的工作状态。 技术装备的精度要求:GNSS接收机、全站仪…...

如何使用C# 读写西门子PLC
在C# WPF应用程序中,与西门子S7系列PLC进行通信是一个常见的需求,尤其是在工业自动化领域。以下是三种实现WPF上位机与西门子S7系列PLC通信同步的方式,每种方式都提供了代码实例、优缺点和使用场景。 1. 使用S7.Net库 代码示例: // 创建PLC连接 var plc = new S7.Net.Pl…...

反向沙箱-安全上网解决方案
随着信息化的发展,企业日常办公越来越依赖互联网。终端以及普通PC终端在访问互联网过程中,会遇到各种各样不容忽视的风险,例如员工主动故意的数据泄漏,后台应用程序偷偷向外部发信息,木马间谍软件的外联,以…...

尚品汇-延迟插件实现订单超时取消(四十五)
目录: (1)延迟插件封装 (2)基于延迟插件测试 如何保证消息幂等性? (3)改造订单service-order模块-实现订单超时取消 (1)延迟插件封装 把消息带过去&#…...

欺诈文本分类检测(十一):LLamaFactory多卡微调
1. 引言 前文训练时都做了一定的编码工作,其实有一些框架可以支持我们零代码微调,LLama-Factory就是其中一个。这是一个专门针对大语言模型的微调和训练平台,有如下特性: 支持常见的模型种类:LLaMA、Mixtral-MoE、Qw…...

SprinBoot+Vue健康管管理微信小程序的设计与实现
目录 1 项目介绍2 项目截图3 核心代码3.1 Controller3.2 Service3.3 Dao3.4 application.yml3.5 SpringbootApplication3.5 Vue3.6 uniapp代码 4 数据库表设计5 文档参考6 计算机毕设选题推荐7 源码获取 1 项目介绍 博主个人介绍:CSDN认证博客专家,CSDN平…...

C++基础类容详解
目录 知识点1 C的概述 1 C的特征 2 C程序的编辑、编译和执行 3 第一个C源程序 4 面向对象程序设计思想 4.1 面向对象程序设计思想初始 4.2 面向对象程序设计思想的核心 知识点2 C对C的扩展 1 作用域访问运算符(::) 2 名称空间域 2.1 创建名称空间域 2.2 已有名称空间…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

Qt的学习(二)
1. 创建Hello Word 两种方式,实现helloworld: 1.通过图形化的方式,在界面上创建出一个控件,显示helloworld 2.通过纯代码的方式,通过编写代码,在界面上创建控件, 显示hello world; …...
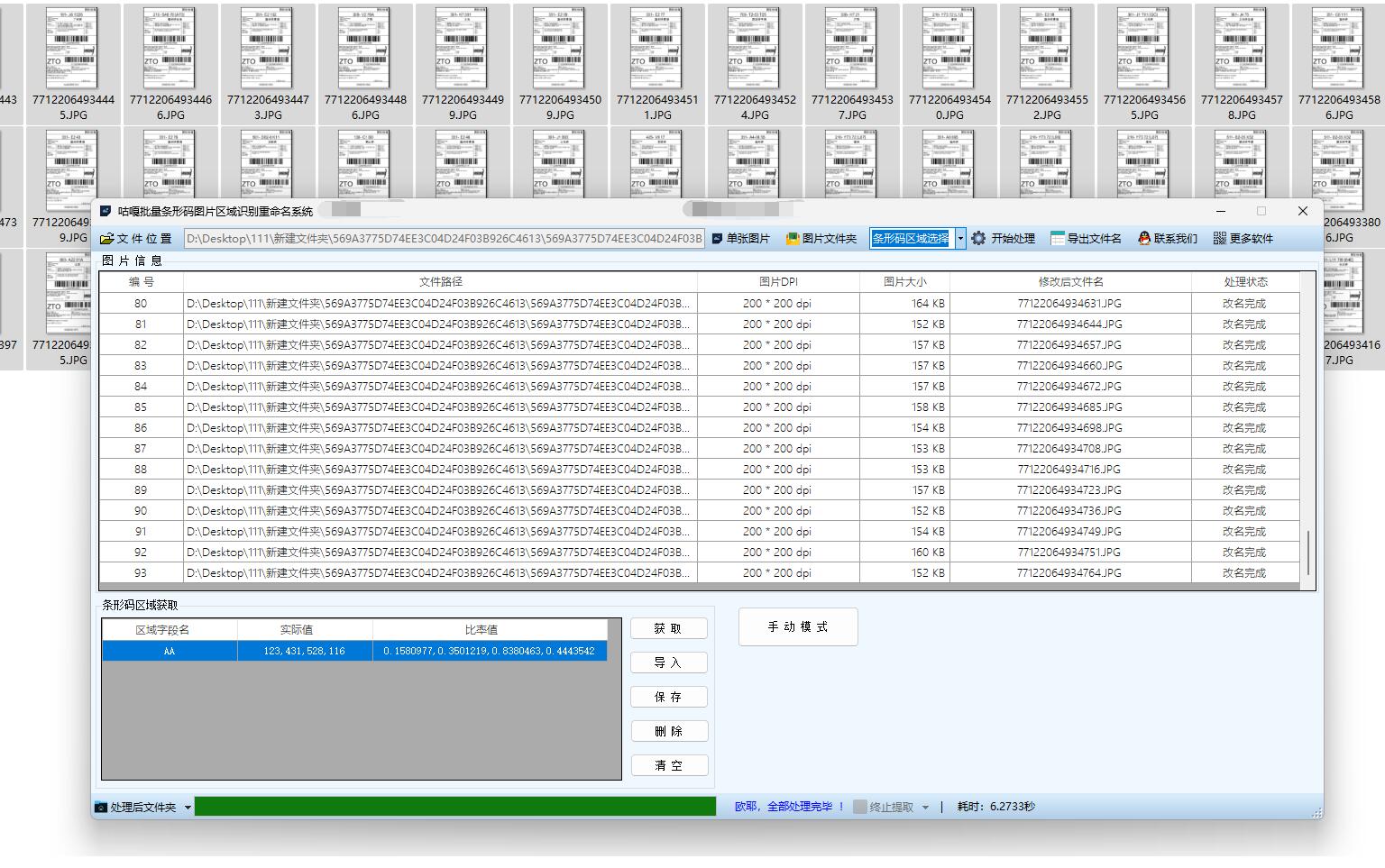
【工具教程】多个条形码识别用条码内容对图片重命名,批量PDF条形码识别后用条码内容批量改名,使用教程及注意事项
一、条形码识别改名使用教程 打开软件并选择处理模式:打开软件后,根据要处理的文件类型,选择 “图片识别模式” 或 “PDF 识别模式”。如果是处理包含条形码的 PDF 文件,就选择 “PDF 识别模式”;若是处理图片文件&…...
