各种各样的正则表达式
一、校验数字的表达式
数字:^[0-9]*$
n位的数字:^\d{n}$
至少n位的数字:^\d{n,}$
m-n位的数字:^\d{m,n}$
零和非零开头的数字:^(0|[1-9][0-9]*)$
非零开头的最多带两位小数的数字:^([1-9][0-9]*)+(.[0-9]{1,2})?$
带1-2位小数的正数或负数:^(\-)?\d+(\.\d{1,2})?$
正数、负数、和小数:^(\-|\+)?\d+(\.\d+)?$
有两位小数的正实数:^[0-9]+(.[0-9]{2})?$
有1~3位小数的正实数:^[0-9]+(.[0-9]{1,3})?$
非零的正整数:^[1-9]\d*$ 或 ^([1-9][0-9]*){1,3}$ 或 ^\+?[1-9][0-9]*$
非零的负整数:^\-[1-9][]0-9″*$ 或 ^-[1-9]\d*$
非负整数:^\d+$ 或 ^[1-9]\d*|0$
非正整数:^-[1-9]\d*|0$ 或 ^((-\d+)|(0+))$
非负浮点数:^\d+(\.\d+)?$ 或 ^[1-9]\d*\.\d*|0\.\d*[1-9]\d*|0?\.0+|0$
非正浮点数:^((-\d+(\.\d+)?)|(0+(\.0+)?))$ 或 ^(-([1-9]\d*\.\d*|0\.\d*[1-9]\d*))|0?\.0+|0$
正浮点数:^[1-9]\d*\.\d*|0\.\d*[1-9]\d*$ 或 ^(([0-9]+\.[0-9]*[1-9][0-9]*)|([0-9]*[1-9][0-9]*\.[0-9]+)|([0-9]*[1-9][0-9]*))$
负浮点数:^-([1-9]\d*\.\d*|0\.\d*[1-9]\d*)$ 或 ^(-(([0-9]+\.[0-9]*[1-9][0-9]*)|([0-9]*[1-9][0-9]*\.[0-9]+)|([0-9]*[1-9][0-9]*)))$
浮点数:^(-?\d+)(\.\d+)?$ 或 ^-?([1-9]\d*\.\d*|0\.\d*[1-9]\d*|0?\.0+|0)$
二、校验字符的表达式
汉字:^[\u4e00-\u9fa5]{0,}$
英文和数字:^[A-Za-z0-9]+$ 或 ^[A-Za-z0-9]{4,40}$
长度为3-20的所有字符:^.{3,20}$
由26个英文字母组成的字符串:^[A-Za-z]+$
由26个大写英文字母组成的字符串:^[A-Z]+$
由26个小写英文字母组成的字符串:^[a-z]+$
由数字和26个英文字母组成的字符串:^[A-Za-z0-9]+$
由数字、26个英文字母或者下划线组成的字符串:^\w+$ 或 ^\w{3,20}$
中文、英文、数字包括下划线:^[\u4E00-\u9FA5A-Za-z0-9_]+$
中文、英文、数字但不包括下划线等符号:^[\u4E00-\u9FA5A-Za-z0-9]+$ 或 ^[\u4E00-
相关文章:

各种各样的正则表达式
一、校验数字的表达式 数字:^[0-9]*$ n位的数字:^\d{n}$ 至少n位的数字:^\d{n,}$ m-n位的数字:^\d{m,n}$ 零和非零开头的数字:^(0|[1-9][0-9]*)$ 非零开头的最多带两位小数的数字:^([1-9][0-9]*)+(.[0-9]{1,2})?$ 带1-2位小数的正数或负数:^(\-)?\d+(\.\d{1,2})?$ 正…...

WebRTC 基础
WebRTC 基础 目录 什么是 WebRTCWebRTC 的基本概念WebRTC 的基本流程 连接建立流程图 WebRTC 的基本对象 RTCPeerConnectionRTCSessionDescriptionRTCIceCandidate WebRTC API 详解 RTCPeerConnection API媒体流 API 详细的代码示例 基本连接示例完整的 WebRTC 实现示例 总结…...

半天攻略:用ChatGPT快速搞定高质量论文,从选题到完稿一站式指南!
在学术论文的撰写过程中,ChatGPT可以作为一个强大的辅助工具,帮助完成从确定主题到整理参考文献的各个环节。接下来,我们将详细介绍如何利用ChatGPT提升论文写作的效率和质量。 确定论文主题 初步探索:通过ChatGPT探索主题&#…...

探索PDF的奥秘:pdfrw库的神奇之旅
文章目录 探索PDF的奥秘:pdfrw库的神奇之旅背景:为何选择pdfrw?pdfrw是什么?如何安装pdfrw?五个简单的库函数使用方法场景应用:pdfrw在实际工作中的应用常见问题与解决方案总结 探索PDF的奥秘:p…...

修改jupyter notebook 默认浏览器(不动配置文件,改系统默认浏览器)
最开始把联想浏览器切到EDGE就是用的修改系统的默认浏览器。不知怎么的现在搜到的方法都是在说修改配置文件😓。 不想动配置文件,平时对默认浏览器没有特殊要求的,可以用这个方法。 这里是把默认浏览器改成联想浏览器,电脑也是联…...

一个基于共享内存的内存数据库:1 介绍
初级代码游戏的专栏介绍与文章目录-CSDN博客 我的github:codetoys,所有代码都将会位于ctfc库中。已经放入库中我会指出在库中的位置。 这些代码大部分以Linux为目标但部分代码是纯C的,可以在任何平台上使用。 源码指引:github源…...

可视化编程 制作在线点名程序,人工和随机生成两种模式
以下是对这段代码的分析: 一、功能概述 这是一个使用 Python 的 Tkinter 库创建的图形用户界面(GUI)应用程序,主要功能是进行在线点名和随机抽奖。可以模拟在一个有六排六列座位布局的场景中进行点名操作和不同规模的随机抽奖。 二、主要函数和变量 窗口设置和变量初始化:…...

pdb在CDB间搬迁 dblink 与rman
create pluggable database <pdb_name> from <pdb_name><dblink> relocate availability max create_file_destxxxxx;-----改变目录 How to relocate a PDB from one CDB to another with minimal down time -12.2 Release (Doc ID 2396518.1) GOAL How to …...

Linux系统中的fork与vfork的区别
目录 一、引言 二、fork与vfork的基本概念 1.fork() 2.vfork() 三、fork与vfork的区别 1.内存分配策略 2.执行顺序 3.性能 4.安全性 四、总结 本文将详细介绍Linux系统中fork与vfork这两个系统调用的区别,帮助读者更好地理解它们在实际编程中的应用。 一、引言…...

特殊类的设计和类型转换
文章目录 特殊类1.请设计一个类,不能被拷贝2. 请设计一个类,只能在堆上创建对象3. 请设计一个类,只能在栈上创建对象 (★)4. 请设计一个类,不能被继承5. 请设计一个类,只能创建一个对象(单例模式…...

ES模块导入、导出学习笔记
ES模块导入、导出学习笔记 1、命名导出、导入1.1、声明时直接导出1.2、先声明,再导出 2、默认导出2.1、声明时直接导出2.2、先声明,再导出 3、命名导出 VS 默认导出3.1、命名导出3.2、默认导出3.3、同时使用 4、使用 as 关键字4.1、在 import 中使用 as4…...
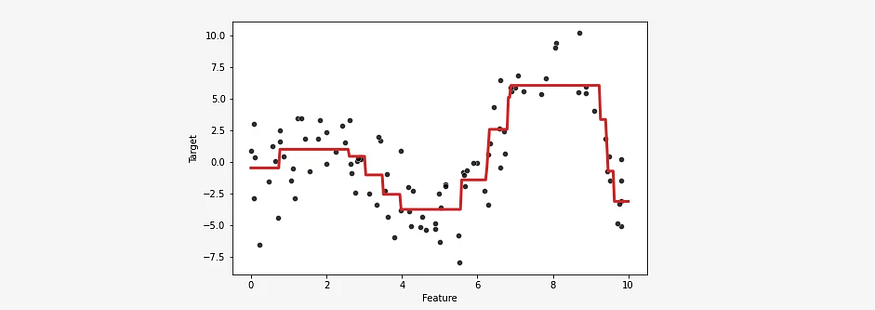
Bagging: 数量,而不是质量。
由 AI 生成:过度简化的树、引导聚合、集成方法、弱学习器、减少方差 集成方法 — 数量,而不是质量 一、说明 机器学习中的集成方法是指组合多个模型以提高预测性能的技术。集成方法背后的基本思想是聚合多个基础模型(通常称为弱学习器&#…...

维信小程序禁止截屏/录屏
一、维信小程序禁止截屏/录屏 //录屏截屏,禁用wx.setVisualEffectOnCapture({visualEffect:hidden});wx.setVisualEffectOnCapture(Object object) 测试安卓手机: 用户截屏,被禁用 用户录屏,录制的是空白内容/黑色内容的视频。 二、微信小…...

不同大模型代码解释对比
包含ChatGPT,讯飞星火,通义千问,腾讯元宝,智谱清言。 目标是想让大模型解释一个用于预处理人体骨骼关节三维坐标数据样本进行填补空帧的Python函数。 def f_padding_none(data):s data.copy()# print(pad the null frames with…...

Python函数的编写
函数实现 首先,我们来看一个简单的Python函数,它使用os和os.path模块来遍历当前目录及其所有子目录,并列出所有文件的名称。 import os def list_all_files(startpath): """ 列出指定路径(包括其子目录ÿ…...

Linux下的常用命令分享 二(ubuntu 16.04)
1、ls -l的返回值说明 以图中为例,说明对于cc.txt.tar.gz文件,文件拥有者即创建该文件的人可以对该文件进行读写操作,但不能执行该文件,文件组成员用户可以进行读写操作,但不能执行该文件,其他用户只可读&…...

FPGA随记——OSERDESE2和IERDESE2
http://t.csdnimg.cn/yNvxf---看这个篇吧 这个挺好的 OSERDESE2 模块要求复位信号高电平有效,并且 需要将异步复位信号同步到串行时钟域。 除了用原语调用,还可以用High Speed SelectIO Wizard这个IP 进行调用 针对具体select IO这个IP的使用和介绍&…...

Xmind思维导图领衔,三款常备神器助你2024年思维升级!
到了2024年,信息多得让人眼花,新东西学都学不完。要在这么多信息里保持清醒,快速学东西,对大家来说是个考验。好在,科技帮了我们大忙,比如思维导图软件,它们直观又灵活,帮我们提高思…...

SEO服务值得吗?提升销售和营销策略的5种方法
在不久之前,搜索引擎优化(SEO)通常被视为一个独立的实体,企业把提升排名和推动自然流量作为重点。随后,AI登场了,让每个人都忙于弄清“游戏”的新规则,一些公司因此质疑SEO服务是否值得。答案是…...

传统CV算法——角点特征点提取匹配算法实战
harris角点 角点可以是两个边缘的角点;角点是邻域内具有两个主方向的特征点;角点通常被定义为两条边的交点,更严格的说,角点的局部邻域应该具有两个不同区域的不同方向的边界。或者说,角点就是多条轮廓线之间的交点。…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
