UniaApp引入Iconfont

一、下载图标资源

1. 登录到阿里巴巴矢量图标库（iconfont）官网（https://www.iconfont.cn/）。
2. 找到你需要的图标并添加到购物车，然后点击购物车图标进入到管理界面，选择 “下载代码”。
3. 在下载选项中选择 “Font class” 方式进行下载，解压下载后的文件。

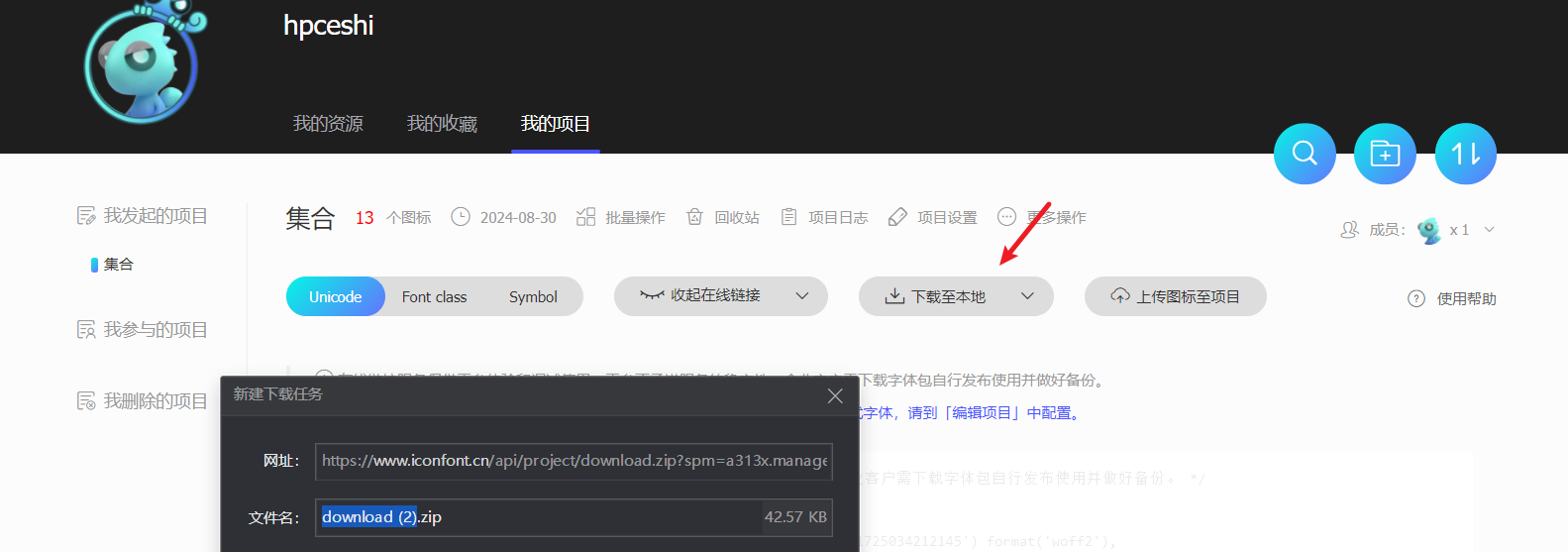
二、将图标文件复制到项目中

1. 将解压后的 iconfont.css（复制到 UniApp 项目的合适位置)

2.官网把这个代码复制下来,替换iconfont.css的这段代码

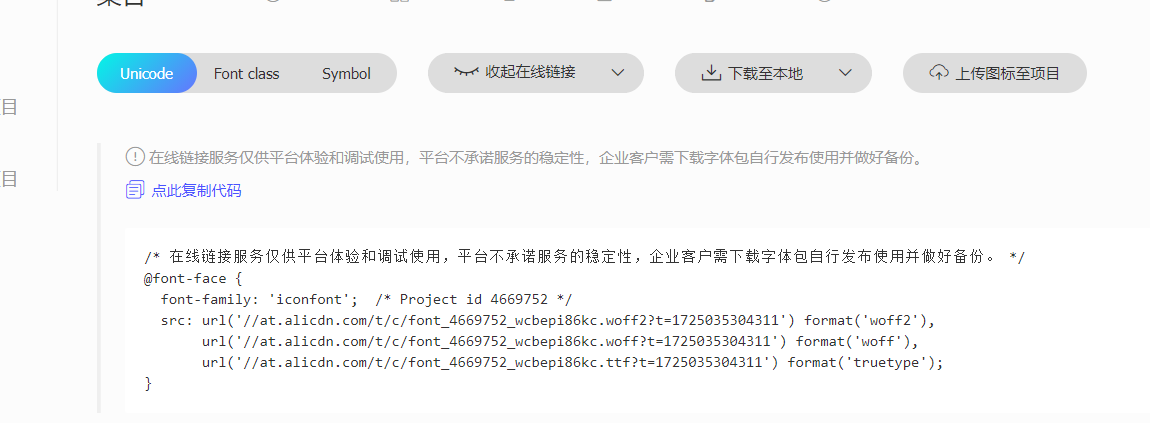
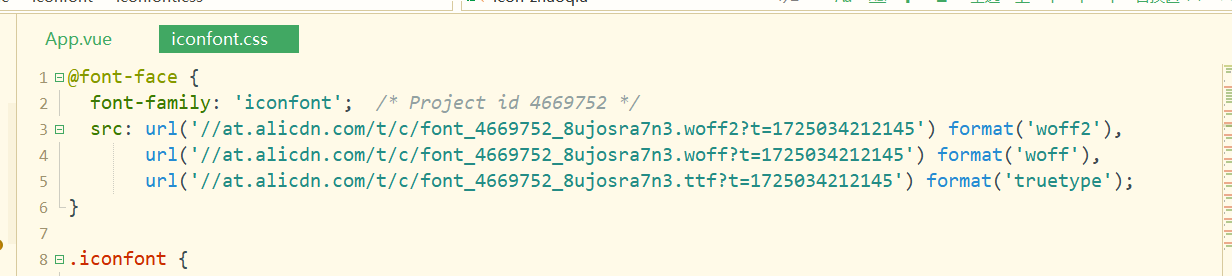
三、在项目中引入 CSS 文件

1. 在需要使用图标的页面的 Vue 文件中或者在项目的全局样式文件中（如 App.vue 中的 style 标签内或者单独的全局 CSS 文件）引入 iconfont.css 文件：

/* 在 App.vue 的 style 标签中或者全局 CSS 文件中 */@import "./assets/iconfont/iconfont.css";

四、使用图标

在页面的模板（template）中，通过 class 来使用图标

<template><view><i class="iconfont icon-your-icon-name"></i></view></template>

其中 icon-your-icon-name 是你在阿里巴巴矢量图标库中对应的图标的类名。
通过以上步骤，就可以在 UniApp 项目中成功引入并使用 iconfont 图标了。

五、小程序底部使用

直接下载png使用即可