在VitePress中进行页面链接:最佳实践与实例
在使用VitePress构建静态网站时,页面之间的链接是必不可少的。本文将介绍如何在VitePress中正确链接页面,包括内部页面和外部非VitePress页面的链接方法,并通过实例代码进行详细解释。
一、链接VitePress内部页面
在VitePress中,你可以使用绝对路径和相对路径来链接不同的页面。为了确保链接的灵活性和维护的便利性,最佳实践是省略文件扩展名(如.md或.html)。这样,VitePress可以根据配置自动生成最终的URL。
实例代码
以下是正确的和错误的链接方式示例:
<!-- 正确的做法 -->
[Getting Started](./getting-started)
[Getting Started](../guide/getting-started)<!-- 错误的做法 -->
[Getting Started](./getting-started.md)
[Getting Started](./getting-started.html)
解释说明
-
正确的做法:
./getting-started:链接到当前目录下的getting-started页面。../guide/getting-started:链接到上一级目录中的guide文件夹下的getting-started页面。
-
错误的做法:
- 直接指定文件扩展名(如
.md或.html)是不推荐的,因为这样做限制了VitePress的灵活性,可能导致链接在生成时出现问题。
- 直接指定文件扩展名(如
二、链接非VitePress页面
如果你的网站中包含不是由VitePress生成的页面,链接到这些页面时需要特别注意。你可以使用完整URL或在Markdown中明确指定目标。
实例代码
-
使用完整URL(将在新标签页中打开):
[Link to pure.html](http://yourwebsite.com/pure.html){target="_blank"} -
使用相对路径并指定目标:
[Link to pure.html](/pure.html){target="_self"}注意:这里的路径是相对于网站根目录的。如果你的页面不在根目录下,你可能需要使用类似
../../pure.html的路径。 -
直接使用HTML锚点标签:
<a href="/pure.html" target="_self">Link to pure.html</a>
解释说明
- 完整URL:这种方式适用于链接到外部网站或你的网站中非VitePress生成的页面,并且希望在新标签页中打开链接。
- 相对路径:当链接到同一域名下的非VitePress页面时,可以使用相对路径。但需要注意路径的正确性,以确保链接能够正确解析。
- HTML锚点标签:在某些情况下,直接使用HTML标签可能更加灵活和直观。
总结
在VitePress中进行页面链接时,应遵循最佳实践,省略文件扩展名,并根据需要选择正确的链接方式。无论是链接VitePress内部页面还是外部非VitePress页面,都应确保路径的正确性和链接的可用性。通过合理使用Markdown和HTML语法,可以轻松实现页面之间的顺畅导航。
相关文章:

在VitePress中进行页面链接:最佳实践与实例
在使用VitePress构建静态网站时,页面之间的链接是必不可少的。本文将介绍如何在VitePress中正确链接页面,包括内部页面和外部非VitePress页面的链接方法,并通过实例代码进行详细解释。 一、链接VitePress内部页面 在VitePress中,…...

Qt/C++百度地图/高德地图/天地图/腾讯地图/谷歌地图/加载绘图工具栏
一、前言说明 在地图中提供一个绘图工具栏,可以便捷的在地图上添加各种覆盖物,比如折线、多边形、矩形、圆形等,然后可以获取这些覆盖物的路径以及中心点等属性。这里有几个小插曲,比如百度地图gl版本默认不提供这个功能…...

Vue2 与 Vue3 的区别有哪些
Vue 2 和 Vue 3 在许多方面都有显著的区别,包括性能、API 设计、功能特性等。以下是它们主要的区别: 1. 响应式系统 Vue 2: 基于 Object.defineProperty: Vue 2 使用 Object.defineProperty 来实现响应式数据。这种方法在处理对象属性时有一定的局限性…...

加锁造成的线程优先级反转
优先级反转(Priority Inversion),也称优先级翻转,一般是在优先级不同的多线程环境中发生。在桌面操作系统中,线程的优先级不是太重要,因此较少见优先级反转的现象。但是,优先级反转是实时操作系统(RTOS)中一个常见的问题,特别是在采用优先级调度算法的系统中。这个问…...

【日常记录-Java】SpringBoot中使用无返回值的异步方法
Author:赵志乾 Date:2024-09-05 Declaration:All Right Reserved!!! 1. 简介 在SpringBoot中,使用Async注解可以很方便地标记一个方法为异步执行。好处是调用者无需等待这些方法完成便可继续执…...
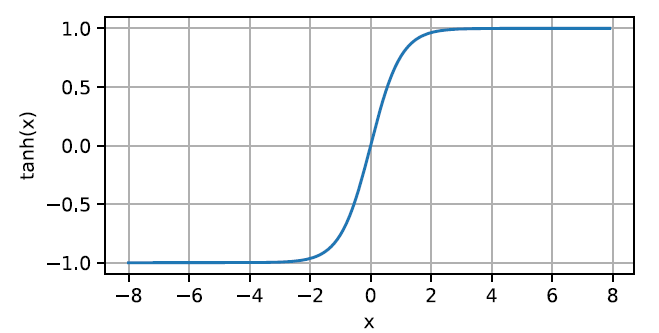
【深度学习】多层感知机的从零开始实现与简洁实现
可以说,到现在我们才真正接触到深度网络。最简单的深度网络称为多层感知机。 多层感知机由多层神经元组成,每一层与它的上一层相连,从中接收输入;同时每一层也与它的下一层相连,影响当前层的神经元。 和以前相同&…...

4、Django Admin对自定义的计算字段进行排序
通常,Django会为模型属性字段,自动添加排序功能。当你添加计算字段时,Django不知道如何执行order_by,因此它不会在该字段上添加排序功能。 如果要在计算字段上添加排序,则必须告诉Django需要排序的内容。你可以通过在…...

rsync搭建全网备份
rsync搭建全网备份 1. 总体概述1.1 目标1.2 简易指导图1.3 涉及工具或命令1.4 环境 2. 实施2.1 配置备份服务器2.2 备份文件准备2.3 整合命令2.4 扩展功能 1. 总体概述 1.1 目标 本次搭建目标: 每天定时把服务器数据备份到备份服务器备份完成后进行校验把过期数据…...

网络安全售前入门09安全服务——安全加固服务
目录 1.服务概述 2.流程及工具 2.1服务流程 2.2服务工具 3.服务内容 4.服务方式 5.风险规避措施 6.服务输出 1.服务概述 安全加固服务是参照风险评估、等保测评、安全检查等工作的结果,基于科学的安全思维方式、长期的安全…...

【Android】GreenDao数据库的使用方式
需求 使用GreenDao数据库进行数据的存储。 介绍 GreenDao 是一个轻量级的对象关系映射(ORM)库,用于简化 Android 应用中的数据库操作。它提供了以下主要功能: 简化数据库操作:通过注解定义实体类,Green…...
)
搜索算法之线性搜索详细解读(附带Java代码解读)
1. 基本概念 线性搜索(Linear Search),也称为顺序搜索,是一种在列表中查找特定元素的算法。它从列表的第一个元素开始,逐个检查每个元素,直到找到目标元素或检查完所有元素。 2. 工作原理 线性搜索的操作…...

Quartz.Net_依赖注入
简述 有时会遇到需要在IJob实现类中依赖注入其他类或接口的情况,但Quartz的默认JobFactory并不能识别具有有参构造函数的IJob实现类,也就无法进行依赖注入 需要被依赖注入的类: public class TestClass {public TestClass(Type jobType, s…...

【系统架构设计师-2011年】综合知识-答案及详解
更多内容请见: 备考系统架构设计师-核心总结索引 文章目录 【第1题】【第2~4题】【第5~7题】【第8题】【第9题】【第10题】【第11题】【第12题】【第13题】【第14题】【第15题】【第16题】【第17题】【第18~19题】【第20~21题】【第22题】【第23题】【第24题】【第25题】【第2…...

World of Warcraft [CLASSIC][80][Grandel]Sapphire Hive Drone
Sapphire Hive Drone 蓝玉虫巢雄蜂 蓝玉虫巢巨峰 索拉查盆地 实用性不强,好看是好看,模型很大,无奈栏位太少...

Unity 对接 Android 第三方广告,App 切换到后台后,再次打开时,第三方广告被销毁导致无法触发回调逻辑的问题
该问题是由发行进行游戏测试时遇到并反馈的。大致情况如下: 1. 当触发了插屏广告后,在关闭广告前将 App 切换到后台,之后再次打开 App,此时插屏广告消失,并切游戏卡死。 2. 当触发激励视频广告后,在广告展…...
,无法及时响应消费者的请求)
Kafka Broker处于高负载状态(例如消息处理量大或系统资源不足),无法及时响应消费者的请求
Caused by: org.apache.kafka.common.errors.TimeoutException: Timeout of 60000ms expired before the position for partition activity-0 could be determined。 出现这个错误的原因是Kafka消费者在尝试获取分区(activity-0)的位置信息时,超时了。在60秒内无法确…...

相关二叉树进阶面试题的讲解?看这一篇足矣
引子:我们在之前学过c语言的二叉树,但是c来做更好!本期要讲的题目如下(其实有点拖欠了,很久之前,就想写这个了,今天终于克服自己的欲望,达成了这个愿望) 1, 二叉树创建字…...

Nginx部署前端Vue项目的深度解析
目录 一、准备工作 1.1 开发环境 1.2 服务器环境 1.3 Nginx安装 二、构建Vue项目 三、上传静态文件到服务器 四、配置Nginx 五、测试并重新加载Nginx 六、访问Vue应用 七、高级配置 7.1 启用HTTPS 7.2 启用Gzip压缩 7.3 缓存控制 八、常见问题与解决方案 8.1 40…...
PHP一站式解决方案高级房产系统小程序源码
一站式解决方案,高级房产系统让房产管理更轻松 🏠【开篇:告别繁琐,迎接高效房产管理新时代】🏠 你是否还在为房产管理的繁琐流程而头疼?从房源录入、客户咨询到合同签订、售后服务,每一个环节…...

轻量级模型解读——EfficientNet系列
EfficientNet自2019年谷歌提出以来,经历了三个版本,2019EfficientNet ——> 2020EfficientNet-Lite——> 2021EfficientNetv2 文章目录 1、EfficientNet2、EfficientNetv23、EfficientNet-Lite 对于EfficientNet和EfficientNetv2的解读可见另外两篇…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
