信息安全数学基础(1)整除的概念
前言
在信息安全数学基础中,整除是一个基础且重要的概念。它涉及整数之间的特定关系,对于理解数论、密码学等领域至关重要。以下是对整除概念的详细阐述:
一、定义
设a, b是任意两个整数,其中b ≠ 0。如果存在一个整数q,使得等式a = q × b成立,那么称b整除a,或者a被b整除,记作b | a。此时,b叫作a的因数,a叫作b的倍数。反之,如果不存在这样的整数q,则称b不能整除a,或a不能被b整除,记作b ∤ a。
二、性质
- 传递性:若a | b且b | c,则a | c。这意味着整除关系具有传递性。
- 线性组合:若c | a且c | b,则对于任意的整数s, t,有c | (s × a + t × b)。这表示c能够整除a和b的线性组合。
- 零和一的特殊性:0是任何非零整数的倍数;1是任何整数的倍数;任何非零整数a是其本身的倍数,也是其自身的因数。
- 素数与合数:若一个正整数n(n ≠ 0, ±1)除了平凡因数±1和±n外,没有其他因数,则n称为素数(或质数、不可约数);否则,n称为合数。
- 素数定理:素数有无穷多个。这意味着无论我们找到多少个素数,都总能找到更多的素数。
三、应用
整除的概念在信息安全数学基础中有着广泛的应用,特别是在密码学领域。例如,在RSA加密算法中,公钥和私钥的生成依赖于大素数的选取和运算。此外,整除还与其他数学工具(如模运算、同余等)紧密相关,共同构成了信息安全数学基础的重要组成部分。
四、示例
- 设a = 12,b = 3。因为12 = 4 × 3,所以3 | 12,即3整除12。
- 设n = 14,它是一个合数,因为除了1和14外,它还有2和7作为因数。
五、总结
综上所述,整除是信息安全数学基础中一个基本而重要的概念,它描述了整数之间的特定关系,并在数论、密码学等领域中发挥着重要作用。
![]() 结语
结语
没有那个人
自己就去做那个人
!!!

相关文章:

信息安全数学基础(1)整除的概念
前言 在信息安全数学基础中,整除是一个基础且重要的概念。它涉及整数之间的特定关系,对于理解数论、密码学等领域至关重要。以下是对整除概念的详细阐述: 一、定义 设a, b是任意两个整数,其中b ≠ 0。如果存在一个整数q࿰…...

SearchGPT与谷歌:早期分析及用户反馈
光年AI系统,作为先进AI技术的成果,推出了一个AI驱动搜素引擎的原型,类似于SearchGPT。 该发布引起了广泛的关注,并引发了关于其是否有能力与Google竞争的讨论。 然而,早期的研究和用户反馈表明,虽然Searc…...

VUE饿了么UPload组件自定义上传
代码: 1.视图: <el-dialog :title"dialogTitle" width"30%" :visible.sync"dialogFormVisible" :destroy-on-close"true"><el-form ref"fileForm" class"items-align" ><e…...

2.1概率统计的世界
欢迎来到概率统计的世界!在量化交易中,概率统计是至关重要的工具。通过理解概率,我们可以用数学的方法来描述市场行为,预测未来走势,并制定交易策略。让我们一起从基础概念开始,逐步深入,揭开概…...

SpringBoot使用QQ邮箱发送邮件
1.开启POP3/IMAP/SMTP/Exchange/CardDAV/CalDAV服务 设置 -> 账号 -> POP3/IMAP/SMTP/Exchange/CardDAV/CalDAV服务 获取授权码 SpringBoot依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter&l…...

使用 OpenCV 和 NumPy 进行图像处理:HSV 范围筛选实现PS抠图效果
使用 OpenCV 和 NumPy 进行图像处理:HSV 范围筛选实现PS抠图效果 在计算机视觉和图像处理领域,OpenCV 是一个非常强大的库,能够帮助我们执行各种图像操作。在这篇博客中,我们将通过一个简单的示例演示如何使用 OpenCV 和 NumPy 来…...

IIS中间件
中间件 中间件是一类软件,为应用程序、服务和组件提供一个通用的服务层。 主要功能 通信:提供通信框架,帮助不同系统与应用之间进行数据交换和通信 事务管理、资源管理 安全服务:提供认证、授权、加密等安全策略 数据访问&a…...

BMP280气压传感器详解(STM32)
目录 一、介绍 二、传感器原理 1.原理图 2.引脚描述 3.传感器数据获取流程 三、程序设计 main.c文件 bmp280.h文件 bmp280.c文件 四、实验效果 五、资料获取 项目分享 一、介绍 BMP280是一款基于博世公司APSM工艺的小封装低功耗数字复合传感器,它可以测…...
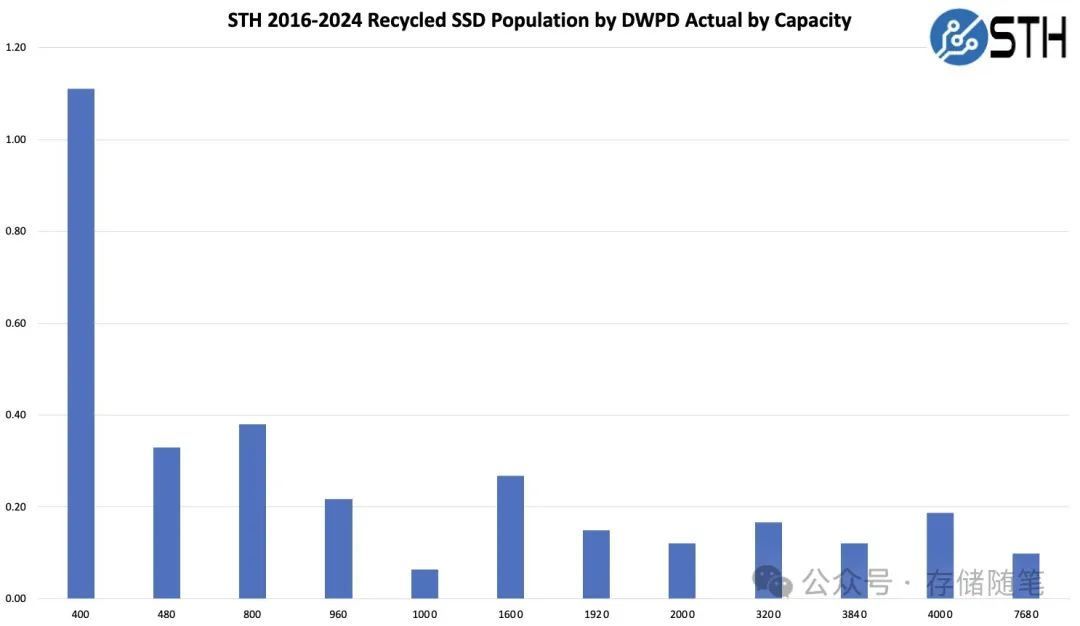
DWPD指标:为何不再适用于大容量SSD?
固态硬盘(Solid State Drives, SSD)作为计算机行业中最具革命性的技术之一,凭借其更快的读写速度、增强的耐用性和能效,已经成为大多数用户的首选存储方案。然而,如同任何其他技术一样,SSD也面临自身的挑战…...

路由器的固定ip地址是啥意思?固定ip地址有什么好处
在当今数字化时代,路由器作为连接互联网的重要设备,扮演着举足轻重的角色。其中,路由器的固定IP地址是一个常被提及但可能让人困惑的概念。下面跟着虎观代理小二一起将深入探讨路由器的固定IP地址的含义,揭示其背后…...

Java——踩坑Arrays.asList()
坑1:不能直接使用 Arrsys.asList() 来转换基本类型数据 public static void test1(){// 1、不能直接使用asList来转换基本类型数组int[] arr {1, 2, 3};List list Arrays.asList(arr);System.out.printf("list:%s size:%s class:%s", list, list.size(…...

前缀列表(ip-prefix)配置
一. 实验简介 本来前缀列表是要和访问控制列表放在一起讲的,但是这里单拎出来是为了更详细的讲解两者的区别 1.前缀列表针对IP比访问控制更加灵活。 2.前缀列表在后面被引用时是无法对数据包进行过滤的 实验拓扑 二. 实验目的 R4路由器中只引入子网LoopBack的…...

每日OJ_牛客_电话号码(简单哈希模拟)
目录 牛客_电话号码(简单哈希模拟) 解析代码 牛客_电话号码(简单哈希模拟) 电话号码__牛客网 解析代码 #include <iostream> #include <unordered_map> #include <set> #include <string> using name…...

鸿蒙轻内核M核源码分析系列十二 事件Event
往期知识点记录: 鸿蒙(HarmonyOS)应用层开发(北向)知识点汇总 轻内核M核源码分析系列一 数据结构-双向循环链表 轻内核M核源码分析系列二 数据结构-任务就绪队列 鸿蒙轻内核M核源码分析系列三 数据结构-任务排序链表 轻…...

基于 RocketMQ 的云原生 MQTT 消息引擎设计
作者:沁君 概述 随着智能家居、工业互联网和车联网的迅猛发展,面向 IoT(物联网)设备类的消息通讯需求正在经历前所未有的增长。在这样的背景下,高效和可靠的消息传输标准成为了枢纽。MQTT 协议作为新一代物联网场景中…...

AWVS/Acunetix Premium V24.8
前言 Acunetix Premium 是一款网络安全 漏洞扫描 工具,主要用于自动化网站漏洞扫描和管理。它的特点包括深度扫描和发现各种类型的漏洞(如 SQL 注入和跨站脚本),支持多种技术和平台,提供详尽的报告和修复建议…...

[数据集][目标检测]灭火器检测数据集VOC+YOLO格式3255张1类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):3255 标注数量(xml文件个数):3255 标注数量(txt文件个数):3255 标注…...

【技术警报】Redis故障启示录:当主节点宕机,如何避免数据“雪崩”?
在高并发的互联网世界中,Redis作为一个高性能的键值存储系统,常被用于缓存、消息队列等场景,为应用提速增效。然而,技术的光芒背后也隐藏着潜在的危机——今天,我们就来探讨一个真实发生的案例:Redis主节点…...

【基础】Three.js加载纹理贴图、加载外部gltf格式文件
1. 模型使用纹理贴图 const geometry new THREE.BoxGeometry(10, 10, 10);const textureLoader new THREE.TextureLoader(); // 创建纹理贴图加载器const texture textureLoader.load("/crate.gif"); // 加载纹理贴图const material new THREE.MeshLambertMater…...

【区块链 + 人才服务】FISCO BCOS 区块链实训和管理平台 | FISCO BCOS应用案例
中博数科 FISCO BCOS 区块链实训和管理平台主要应用于区块链领域的教育和实训,目的是为学生、教师等用户 提供高效的区块链技术学习和实践体验,同时也为学校提供了一套完整的区块链解决方案。 该平台提供了一套完整的区块链课程体系,包括理论…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...
