统计学习方法与实战——统计学习方法之感知机

、

感知机

1. 感知机是根据输入实例的特征向量 $x$ 对其进行二㺯分尖的线性分光模型:
   $$f(x)=\mathrm{sign}(w\cdot x+b)$$
   感知机模型对应于输入空间 (特征空间) 中的分离超平面 $w\cdot x+b=0$ 。
2. 感知机学习的策略是极小化损失函数:
   $$\underset{w,b}{\min }L(w,b)=-\sum _{x_i\in M}{y}_i\left(w\cdot x_i+b\right)$$
   损失函数对应于误分类点到分离超平面的总距离。
3. 感知机学习算法是基于随机梯度下降法的对损失函数的最优化算法，有原始形式和对偶形式。算法简单且易于实现。原始形式中，首先任意选取一个超平面， 然后用梯度下降法不断极小化目标函数。在这个过程中一次随机选取一个误分类点使其梯度下降。
   $$k⩽{\left(\frac{R}{\gamma }\right)}^2$$
   当训练数据集线性可分时，感知机学习算法存在无穷多个解，其解由于不同的初值或不同的迭代顺序而可能有所不同。
   一分类模菖
   $$\begin{array}{rl}& f(x)=\mathrm{sign}(w\cdot x+b)\\ & \mathrm{sign}(x)=\{\begin{array}{ll}+1,& x⩾0\\ -1,& x<0\end{array}\end{array}$$
   给定训练集:
   T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\} T={(x1​,y1​),(x2​,y2​),⋯,(xN​,yN​)}
   定义感知机的损失函数
   $$L(w,b)=-\sum _{x_i\in M}{y}_i\left(w\cdot x_i+b\right)$$
   算法
   随机梯度下降法 Stochastic Gradient Descent
   随机抽取一个点使其梯度下降。
   $$\begin{array}{rl}& w=w+\eta y_i{x}_i\\ & b=b+\eta y_i\end{array}$$
   当实例点被误分类，即位于分离超平面的错误侧，则调整 $w,b$ 的值，使分离超平面向该无分类点的一侧移动，直至误分类点被正确分类

三要素分析

模型

输入空间：$\mathcal{X}\subseteq {\mathbf{R}}^{\mathbf{n}}$

输出空间：$\mathcal{Y}=+1,-1$

决策函数：$f(x)=sign(w\cdot x+b)$

策略

确定学习策略就是定义**(经验)**损失函数并将损失函数最小化。

注意这里提到了经验，所以学习是base在训练数据集上的操作

损失函数选择

损失函数的一个自然选择是误分类点的总数，但是，这样的损失函数不是参数$w,b$的连续可导函数，不易优化

损失函数的另一个选择是误分类点到超平面$S$的总距离，这是感知机所采用的

感知机学习的经验风险函数(损失函数)
$$L(w,b)=-\sum _{x_i\in M}{y}_i(w\cdot x_i+b)$$
其中$M$是误分类点的集合

给定训练数据集$T$，损失函数$L(w,b)$是$w$和$b$的连续可导函数

算法

原始形式

输入： T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x N , y N ) } T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{N}, y_{N}\right)\right\} T={(x1​,y1​),(x2​,y2​),…,(xN​,yN​)}
x i ∈ X = R n , y i ∈ Y = { − 1 , + 1 } , i = 1 , 2 , … , N ; 0 < η ⩽ 1 x_{i} \in \mathcal{X}=\mathbf{R}^{\mathbf{n}}, \mathbf{y}_{\mathbf{i}} \in \mathcal{Y}=\{-1,+1\}, i=1,2, \ldots, \mathcal{N} ; 0<\eta \leqslant 1 xi​∈X=Rn,yi​∈Y={−1,+1},i=1,2,…,N;0<η⩽1

输出：$w,b;f(x)=sign(w\cdot x+b)$

1. 选取初值$w_0,b_0$

2. 训练集中选取数据$(x_i,y_i)$

3. 如果$y_i(w\cdot x_i+b)⩽0$
   $w\leftarrow w+\eta y_i{x}_i$
   $b\leftarrow b+\eta y_i$

4. 转至(2)，直至训练集中没有误分类点

注意这个原始形式中的迭代公式，可以对$x$补1，将$w$和$b$合并在一起，合在一起的这个叫做扩充权重向量，书上有提到。

对偶形式

对偶形式的基本思想是将$w$和$b$表示为实例$x_i$和标记$y_i$的线性组合的形式，通过求解其系数而求得$w$和$b$。
算法流程：

输入： T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x N , y N ) } T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{N}, y_{N}\right)\right\} T={(x1​,y1​),(x2​,y2​),…,(xN​,yN​)}
x i ∈ X = R n , y i ∈ Y = { − 1 , + 1 } , i = 1 , 2 , … , N ; 0 < η ⩽ 1 x_{i} \in \mathcal{X}=\mathbf{R}^{\mathbf{n}}, \mathbf{y}_{\mathbf{i}} \in \mathcal{Y}=\{-1,+1\}, i=1,2, \ldots, \mathcal{N} ; 0<\eta \leqslant 1 xi​∈X=Rn,yi​∈Y={−1,+1},i=1,2,…,N;0<η⩽1

输出：
$\begin{array}{rl}\alpha ,b;f(x)& =\mathrm{sign}\left(\sum _{j=1}^N{\alpha }_j{y}_j{x}_j\cdot x+b\right)\\ \alpha >& ={\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_N\right)}^T\end{array}$

1. $\alpha \leftarrow 0,b\leftarrow 0$

2. 训练集中选取数据$(x_i,y_i)$

3. 如果$y_i\left({\sum }_{j=1}^N{\alpha }_j{y}_j{x}_j\cdot x+b\right)⩽0$

$$\begin{gathered} {\alpha }_i\leftarrow {\alpha }_i+\eta \\ b\leftarrow b+\eta y_i \end{gathered}$$

4. 转至(2)，直至训练集中没有误分类点

Gram matrix

对偶形式中，训练实例仅以内积的形式出现。

为了方便可预先将训练集中的实例间的内积计算出来并以矩阵的形式存储，这个矩阵就是所谓的Gram矩阵

$G={\left[x_i\cdot x_j\right]}_{N\times N}$

相关问题

题中问考虑损失函数最值的时候，不会有影响么？

1. 感知机处理线性可分数据集，二分类， Y = { + 1 , − 1 } \mathcal{Y}=\{+1,-1\} Y={+1,−1}，所以涉及到的乘以$y_i$ 的操作实际贡献的是符号；

2. 损失函数 $L(w,b)=-{\sum }_{x_i\in M}{y}_i(w\cdot x_i+b)$,其中 $M$ 是错分的点集合，线性可分的数据集肯定能找到超平面 $S$， 所以这个损失函数最值是0。

3. 如果正确分类， $y_i(w\cdot x_i+b)=|w\cdot x_i+b|$ ，错误分类的话，为了保证正数就加个负号，这就是损失函数里面那个负号，这个就是函数间隔；

4. $\frac{1}{||w||}$ 用来归一化超平面法向量，得到几何间隔，也就是点到超平面的距离， 函数间隔和几何间隔的差异在于同一个超平面 $(w,b)$ 参数等比例放大成 $(kw,kb)$ 之后，虽然表示的同一个超平面，但是点到超平面的函数间隔也放大了，但是几何间隔是不变的；

5. 具体算法实现的时候， $w$要初始化，然后每次迭代针对错分点进行调整，既然要初始化，那如果初始化个 $||w||=1$ 的情况也就不用纠结了，和不考虑 $\frac{1}{||w||}$ 是一样的了；

6. 针对错分点是这么调整的

   $\begin{array}{rl}w& \leftarrow w+\eta y_i{x}_i\\ b& \leftarrow b+\eta y_i\end{array}$

   前面说了 $y_i$ 就是个符号，那么感知机就可以解释为针对误分类点，通过调整 $w,b$ 使得超平面向该误分类点一侧移动，迭代这个过程最后全分类正确；

7. 感知机的解不唯一，和初值有关系，和误分类点调整顺序也有关系；

8. 这么调整就能找到感知机的解？能，Novikoff还证明了，通过有限次搜索能找到将训练数据完全正确分开的分离超平面。

例子

iris数据集分类实战

数据集查看

import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt#  load data
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label'
]
df.label.value_counts()
plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

• 数据集显示
  

data = np.array(df.iloc[:100, [0, 1, -1]])
X, y = data[:,:-1], data[:,-1]
y = np.array([1 if i == 1 else -1 for i in y])
# 数据线性可分，二分类数据
# 此处为一元一次线性方程
class Model:def __init__(self):self.w = np.ones(len(data[0]) - 1, dtype=np.float32)self.b = 0self.l_rate = 0.1# self.data = datadef sign(self, x, w, b):y = np.dot(x, w) + breturn y# 随机梯度下降法def fit(self, X_train, y_train):is_wrong = Falsewhile not is_wrong:wrong_count = 0for d in range(len(X_train)):X = X_train[d]y = y_train[d]if y * self.sign(X, self.w, self.b) <= 0:self.w = self.w + self.l_rate * np.dot(y, X)self.b = self.b + self.l_rate * ywrong_count += 1if wrong_count == 0:is_wrong = Truereturn 'Perceptron Model!'
perceptron = Model()
perceptron.fit(X, y)x_points = np.linspace(4, 7, 10)
y_ = -(perceptron.w[0] * x_points + perceptron.b) / perceptron.w[1]
plt.plot(x_points, y_)plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

显示结果

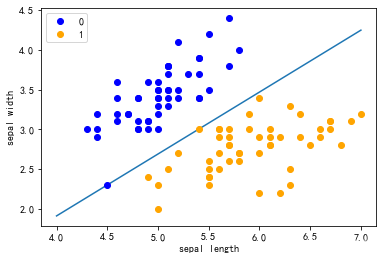
sklearn 实战感知机

import sklearn
from sklearn.linear_model import Perceptron
clf = Perceptron(fit_intercept=True, max_iter=1000, shuffle=True)
clf.fit(X, y)
print(clf.coef_)
# 截距 Constants in decision function.
print(clf.intercept_)
# 画布大小
plt.figure(figsize=(10,10))# 中文标题
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.title('鸢尾花线性数据示例')plt.scatter(data[:50, 0], data[:50, 1], c='b', label='Iris-setosa',)
plt.scatter(data[50:100, 0], data[50:100, 1], c='orange', label='Iris-versicolor')# 画感知机的线
x_ponits = np.arange(4, 8)
y_ = -(clf.coef_[0][0]*x_ponits + clf.intercept_)/clf.coef_[0][1]
plt.plot(x_ponits, y_)# 其他部分
plt.legend()  # 显示图例
plt.grid(False)  # 不显示网格
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

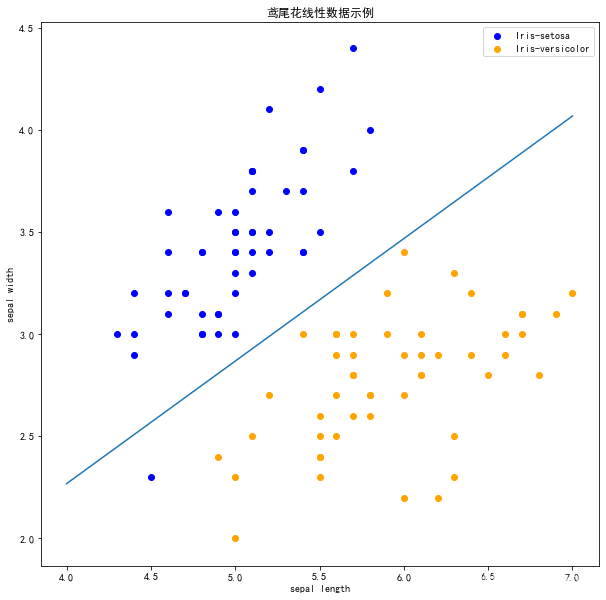
在上图中，有一个位于左下角的蓝点没有被正确分类，这是因为 SKlearn 的 Perceptron 实例中有一个tol参数。

tol 参数规定了如果本次迭代的损失和上次迭代的损失之差小于一个特定值时，停止迭代。所以我们需要设置 tol=None 使之可以继续迭代：

clf = Perceptron(fit_intercept=True, max_iter=1000,tol=None,shuffle=True)
clf.fit(X, y)# 画布大小
plt.figure(figsize=(10,10))# 中文标题
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.title('鸢尾花线性数据示例')plt.scatter(data[:50, 0], data[:50, 1], c='b', label='Iris-setosa',)
plt.scatter(data[50:100, 0], data[50:100, 1], c='orange', label='Iris-versicolor')# 画感知机的线
x_ponits = np.arange(4, 8)
y_ = -(clf.coef_[0][0]*x_ponits + clf.intercept_)/clf.coef_[0][1]
plt.plot(x_ponits, y_)# 其他部分
plt.legend()  # 显示图例
plt.grid(False)  # 不显示网格
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

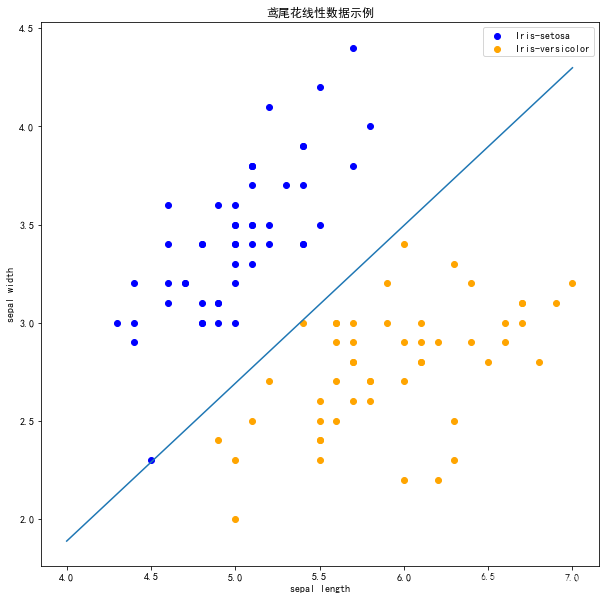
习题解答

习题2.1

Minsky 与 Papert 指出：感知机因为是线性模型，所以不能表示复杂的函数，如异或 (XOR)。验证感知机为什么不能表示异或。

1. 列出异或函数(XOR)的输入和输出；
2. 使用图例法证明异或问题是线性不可分的；
3. 使用反证法证明感知机无法表示异或。

解题步骤

异或函数(XOR)的输入和输出
对于异或函数(XOR)，全部的输入与对应的输出如下：
$$\begin{array}{ccc}{x}_1& x_2& y=x_1\oplus x_2\\ 0& 0& -1\\ 0& 1& 1\\ 1& 0& 1\\ 1& 1& -1\end{array}$$

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline# 使用Dataframe表示异或的输入与输出数据
x1 = [0, 0, 1, 1]
x2 = [0, 1, 0, 1]
y = [-1, 1, 1, -1]
x1 = np.array(x1)
x2 = np.array(x2)
y = np.array(y)
data = np.c_[x1, x2, y]
data = pd.DataFrame(data, index=None, columns=['x1', 'x2', 'y'])
data.head()
# 获取正类别（y=1）的数据
positive = data.loc[data['y'] == 1]
# 获取负类别（y=-1）的数据
negative = data.loc[data['y'] == -1]# 绘制数据图
# 绘制坐标轴
plt.xlim(-0.5, 1.5)
plt.ylim(-0.5, 1.5)
plt.xticks([-0.5, 0, 1, 1.5])
plt.yticks([-0.5, 0, 1, 1.5])
# 添加坐标轴文字
plt.xlabel("x1")
plt.ylabel("x2")
# 绘制正、负样本点
plt.plot(positive['x1'], positive['x2'], "ro")
plt.plot(negative['x1'], negative['x2'], "bx")
# 添加图示
plt.legend(['Positive', 'Negative'])
plt.show()

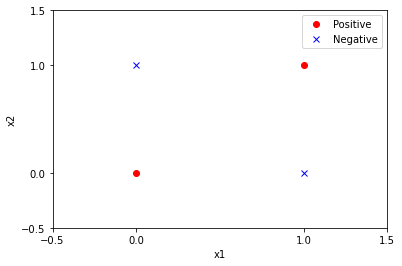
 从上图可以看出，无法使用一条直线将两类样本分开，所以异或问题是线性不可分的
 
 下一步，使用感知机模型进行测试w，b

from sklearn.linear_model import Perceptron
import numpy as np# 构造异或问题的训练数据集
X_train = np.array([[1, 1], [1, 0], [0, 1], [0, 0]])
y = np.array([-1, 1, 1, -1])# 使用sklearn的Perceptron类构建感知机模型
perceptron_model = Perceptron()
# 进行模型训练
perceptron_model.fit(X_train, y)# 打印模型参数
print("感知机模型的参数：w=", perceptron_model.coef_[0], "b=", perceptron_model.intercept_[0])

感知机模型的参数：w= [0. 0.] b= 0.0

反证法

$f(x)=\mathrm{sign}(w\cdot x+b)$
$\mathrm{sign}(x)=\{\begin{array}{ll}+1,& x⩾0\\ -1,& x<0\end{array}$

假设咸知机模型可以表示异或问题，即满足异或函数(XOR)输入与输出的情况（见第 $1步$ )。假设 $x$ 向量只有两个维度 $x_1,x_2$ :

1. 根据 $x_1=0,x_2=0,f(x)=-1$ ，则 $w\cdot x+b<0$ ，可得 $b<0$ ；
2. 根据 $x_1=0,x_2=1,f(x)=1$ ，则 $w_2+b>0$ ，结合 $b<0$ ，可得 $w_2>-b>0$;
3. 根据 $x_1=1,x_2=0,f(x)=1$, 则 $w_1+b>0$ ，结合 $b<0$ ，可得 $w_1>-b>0$;
4. 根据 $x_1=1,x_2=1$ ，并结合 $w_1+b>0、w_2>0$ ，则 $w_1+w_2+b>0$ ，可得 $f(x)=1$ ，与异或条件中的 $f(x)=-1$ 矛盾。
5. 所以假设不成立，原命题成立，即感知机模型不能表示异或。

习题2.2

解题步骤在上面的iris数据中已经体现。

import numpy as np
from matplotlib import pyplot as plt
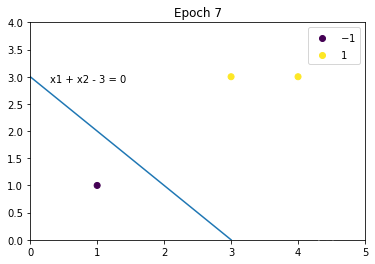
%matplotlib tkclass Perceptron:def __init__(self, X, Y, lr=0.001, plot=True):"""初始化感知机:param X: 特征向量:param Y: 类别:param lr: 学习率:param plot: 是否绘制图形"""self.X = Xself.Y = Yself.lr = lrself.plot = plotif plot:self.__model_plot = self._ModelPlot(self.X, self.Y)self.__model_plot.open_in()def fit(self):# (1)初始化weight, bweight = np.zeros(self.X.shape[1])b = 0# 训练次数train_counts = 0# 分类错误标识mistake_flag = Truewhile mistake_flag:# 开始前，将mistake_flag设置为False，用于判断本次循环是否有分类错误mistake_flag = False# (2)从训练集中选取x,yfor index in range(self.X.shape[0]):if self.plot:self.__model_plot.plot(weight, b, train_counts)# 损失函数loss = self.Y[index] * (weight @ self.X[index] + b)# (3)如果损失函数小于0，则该点是误分类点if loss <= 0:# 更新weight, bweight += self.lr * self.Y[index] * self.X[index]b += self.lr * self.Y[index]# 训练次数加1train_counts += 1print("Epoch {}, weight = {}, b = {}, formula: {}".format(train_counts, weight, b, self.__model_plot.formula(weight, b)))# 本次循环有误分类点（即分类错误），置为Truemistake_flag = Truebreakif self.plot:self.__model_plot.close()# (4)直至训练集中没有误分类点return weight, bclass _ModelPlot:def __init__(self, X, Y):self.X = Xself.Y = Y@staticmethoddef open_in():# 打开交互模式，用于展示动态交互图plt.ion()@staticmethoddef close():# 关闭交互模式，并显示最终的图形plt.ioff()plt.show()def plot(self, weight, b, epoch):plt.cla()# x轴表示x1plt.xlim(0, np.max(self.X.T[0]) + 1)# y轴表示x2plt.ylim(0, np.max(self.X.T[1]) + 1)# 画出散点图，并添加图示scatter = plt.scatter(self.X.T[0], self.X.T[1], c=self.Y)plt.legend(*scatter.legend_elements())if True in list(weight == 0):plt.plot(0, 0)else:x1 = -b / weight[0]x2 = -b / weight[1]# 画出分离超平面plt.plot([x1, 0], [0, x2])# 绘制公式text = self.formula(weight, b)plt.text(0.3, x2 - 0.1, text)plt.title('Epoch %d' % epoch)plt.pause(0.01)@staticmethoddef formula(weight, b):text = 'x1 ' if weight[0] == 1 else '%d*x1 ' % weight[0]text += '+ x2 ' if weight[1] == 1 else ('+ %d*x2 ' % weight[1] if weight[1] > 0 else '- %d*x2 ' % -weight[1])text += '= 0' if b == 0 else ('+ %d = 0' %b if b > 0 else '- %d = 0' % -b)return text

X = np.array([[3, 3], [4, 3], [1, 1]])
Y = np.array([1, 1, -1])
model = Perceptron(X, Y, lr=1)
weight, b = model.fit()

习题2.3

证明以下定理：样本集线性可分的充分必要条件是正实例点所构成的凸壳与负实例点所构成的凸壳互不相交。

1. 写出凸壳和线性可分的定义
2. 证明必要性：线性可分\Rightarrow⇒凸壳不相交
3. 证明充分性：凸壳不相交\Rightarrow⇒线性可分

凸壳

设集合 $S\subset R^n$ ，是由 $R^n$ 中的 $k$ 个点所组成的集合，即 S = { x 1 , x 2 , ⋯ , x k } S=\left\{x_{1}, x_{2}, \cdots, x_{k}\right\} S={x1​,x2​,⋯,xk​} 。定义 $S$ 的凸壳 $\mathrm{conv}(S)$ 为:
$$\mathrm{conv}(S)=\left\{x=\sum _{i=1}^k{\lambda }_i{x}_i\mid \sum _{i=1}^k{\lambda }_i=1,{\lambda }_i⩾0,i=1,2,\cdots ,k\right\}$$

线性可分

给定一个数据集
T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x n , y n ) } T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{n}, y_{n}\right)\right\} T={(x1​,y1​),(x2​,y2​),⋯,(xn​,yn​)}
其中 x i ∈ X = R n , y i ∈ Y = { + 1 , − 1 } , i = 1 , 2 , ⋯ , n x_{i} \in \mathcal{X}=R_{n}, y_{i} \in \mathcal{Y}=\{+1,-1\}, i=1,2, \cdots, n xi​∈X=Rn​,yi​∈Y={+1,−1},i=1,2,⋯,n ，如果存在某个超平面 $S$
$$w\cdot x+b=0$$
能够将数据集的正实例点和负实例点完全正确划分到超平面的两侧，即对所有 $y_i=+1$ 的实例 $i$ ，有 $w\cdot x_i+b>0$ ，对 $y_i=-1$ 的实例 $i$ ，有 $w\cdot x_i+b<0$ ，则称数据集 $T$ 为线性可分 数据集，否则称数据集 $T$ 线性不可分。

线性可分证明凸壳不相交

证明思路（反证法）：

假设原命题不成立：样本集线性可分，正实例点所构成的凸壳与负实例点所构成的凸壳相交
条件推理
发现矛盾，得出原命题成立

1. 假设原命题不成立:
   设数据集 $T$ 中的正例点集为 $S_{+}，S_{+}$的凸壳为 $\mathrm{conv}\left(S_{+}\right)$，负实例点集为 $S_{-}，S_{-}$的凸壳为 $\mathrm{conv}\left(S_{-}\right)$。
   假设样本集线性可分，正实例点所构成的凸壳与负实例点所构成的凸壳相交，即存在某个元素 $s$ ，同时满足 $s\in \mathrm{conv}\left(S_{+}\right)$和 $s\in \mathrm{conv}\left(S_{-}\right)$。
2. 条件推理:
   若数据集 $T$ 是线性可分的，根据线性可分的定义，则存在一个超平面能够将 $S_{+}$和 $S_{-}$完全分离:
   $$w\cdot x+b=0$$
   对于所有的正例点 $x_i$ ，有
   $$w\cdot x_i+b={\epsilon }_i>0,i=1,2,\cdots ,\left|S_{+}\right|$$
   根据凸壳的定义，对于 $\mathrm{conv}\left(S_{+}\right)$中的元素 $s_{+}$，有
   $$\begin{array}{rl}w\cdot s_{+}+b& =w\cdot \left(\sum _{i=1}^{|S_{+}|}{\lambda }_i{x}_i\right)+b\\ & =\left(\sum _{i=1}^{|S_{+}|}{\lambda }_i\left({\epsilon }_i-b\right)\right)+b\\ & =\sum _{i=1}^{|S_{+}|}{\lambda }_i{\epsilon }_i-\left(b\sum _{i=1}^{|S_{+}|}{\lambda }_i\right)+b\left(\because \sum _{i=1}^{|S_{+}|}{\lambda }_i=1\right)\\ & =\sum _{i=1}^{|S_{+}|}{\lambda }_i{\epsilon }_i\end{array}$$
   因此 $w\cdot s_{+}+b={\sum }_{i=1}^{|S_{+}|}{\lambda }_i{\epsilon }_i>0$ 。
   同理对于 $S_{-}$中的元素 $s_{-}$，有 $w\cdot s_{-}+b={\sum }_{i=1}^{|S_{-}|}{\lambda }_i{\epsilon }_i<0$
3. 找出矛盾，得出原命题成立:
   根据条件推理，当 $s\in \mathrm{conv}\left(S_{+}\right)$有 $w\cdot s+b={\sum }_{i=1}^{|S_{+}|}{\lambda }_i{\epsilon }_i>0$ ，当 $s\in \mathrm{conv}\left(S_{-}\right)$有 $w\cdot s+b={\sum }_{i=1}^{|S_{-}|}{\lambda }_i{\epsilon }_i<0$ ，既 $s$ 不可能同时满足若 $s\in \mathrm{conv}\left(S_{+}\right)$和 $s\in \mathrm{conv}\left(S_{-}\right)$，这与假设命题 矛盾。
   因此，原命题成立，当样本线性可分时， $\mathrm{conv}\left(S_{+}\right)$和 $\mathrm{conv}\left(S_{-}\right)$必不相交。必要性得证。

证明充分性：凸壳不相交\Rightarrow⇒线性可分

证明思路：

根据凸壳不相交，找到一个超平面
证明这个超平面可将两个互不相交的凸壳分隔开（反证法）
上述超平面可以将凸壳分隔开，则样本集满足线性可分

证明步骤

1. 根据凸壳不相交，找到一个超平面:
   设数据集 $T$ 中的正例点集为 $S_{+}，S_{+}$的凸壳为 $\mathrm{conv}\left(S_{+}\right)$，负实例点集为 $S_{-}，S_{-}$的凸壳为 $\mathrm{conv}\left(S_{-}\right)$，且conv $\left(S_{+}\right)$与 $\mathrm{conv}\left(S_{-}\right)$不相交。
   定义两个点 $x_1,x_2$ 的距离为
   $$\mathrm{dist}\left(x_1,x_2\right)={\Vert x_1-x_2\Vert }_2$$
   定义 $\mathrm{conv}\left(S_{+}\right)、\mathrm{conv}\left(S_{-}\right)$的距离是，分别处于两个凸壳集合中的点的距离最小值:
   $$\mathrm{dist}\left(\mathrm{conv}\left(S_{+}\right),\mathrm{conv}\left(S_{-}\right)\right)=\min {\Vert s_{+}-s_{-}\Vert }_2{s}_{+}\in \mathrm{conv}\left(S_{+}\right),s_{-}\in \mathrm{conv}\left(S_{-}\right)$$
   记最小值点分别为 $x_{+},x_{-}$， 即：
   $$\mathrm{dist}\left(\mathrm{conv}\left(S_{+}\right),\mathrm{conv}\left(S_{-}\right)\right)=\mathrm{dist}\left(x_{+},x_{-}\right)x_{+}\in \mathrm{conv}\left(S_{+}\right),x_{-}\in \mathrm{conv}\left(S_{-}\right)$$
   定义以 $\left(x_{+},x_{-}\right)$为法线，且过两点中点的超平面为 $f(x\mid w,b)=0$, 则参数为:
   $$\begin{array}{rl}f(x\mid w,b)& ={\left(x_{+}-x_{-}\right)}^T\left(x-\frac{x_{+}+x_{-}}{2}\right)\\ \{\begin{array}{rl}w& ={\left(x_{+}-x_{-}\right)}^T\\ b& =-\frac{1}{2}\left({\Vert x_{+}\Vert }_2^2-{\Vert x_{-}\Vert }_2^2\right)\end{array}& \end{array}$$
2. 证明这个超平面可将两个互不相交的凸壳分隔开 (反证法)
   若某个超平面可将两个互不相交的凸壳分隔开，则 $f(x)\ge 0,x\in \mathrm{conv}\left(S_{+}\right)$且 $f(x)\le 0,x\in \mathrm{conv}\left(S_{-}\right)$。
   $$\begin{array}{rl}f(x)& ={\left(x_{+}-x_{-}\right)}^T\left(x-\frac{x_{+}+x_{-}}{2}\right)\\ & ={\left(x_{+}-x_{-}\right)}^T\left(x+x_{+}-x_{+}-\frac{x_{+}+x_{-}}{2}\right)\\ & ={\left(x_{+}-x_{-}\right)}^T\left(x-x_{+}+\frac{x_{+}-x_{-}}{2}\right)\\ & ={\left(x_{+}-x_{-}\right)}^T\left(x-x_{+}\right)+\frac{{\Vert x_{+}-x_{-}\Vert }_2^2}{2}\end{array}$$
   假设原命题不成立：当 $x\in \mathrm{conv}\left(S_{+}\right)$时，假设 $f(x)<0$ ，则有:
   $${\left(x_{+}-x_{-}\right)}^T\left(x-x_{+}\right)<0$$
   设点 $u=x_{+}+t\left(x-x_{+}\right),t\in [0,1]$ ，即 $u$ 在 $x_{+}$和 $x$ 的线段上。根据凸壳定义, $u\in \mathrm{conv}\left(S_{+}\right)$。则 $u$ 和 $x_{-}$距离的平方为:
   $$\begin{array}{rl}g(t)& ={\Vert u-x_{-}\Vert }_2{}^2\\ & ={\Vert x_{+}+t\left(x-x_{+}\right)-x_{-}\Vert }_2{}^2\end{array}$$

求解 $u$ 和 $x_{-}$距离的最小值, 对上式求导:
$$\begin{array}{rl}{g}^{\prime }(t)& =2\left(x_{+}+t\left(x-x_{+}\right)-x_{-}\right)\left(x-x_{+}\right)\\ & =2{\left(x_{+}-x_{-}\right)}^T\left(x-x_{+}\right)+t{\Vert x-x_{+}\Vert }_2{}^2\end{array}$$
根据假设，在 $t=0$ 时，得 $g^{\prime }(t)<0$ 。在当 $t$ 足够接近于 0 时 (导函数在 0 处的极限值为负，则存在邻域函数递减)，即 $g(t)<g(0)$ 。
$\therefore$ 存在一点 $u$ ，使得它到 $x_{-}$的距离，比定义的凸壳距离 $\mathrm{dist}\left(x_{+},x_{-}\right)$还小。产生矛盾。
故原命题成立，即 $f(x)\ge 0,x\in \mathrm{conv}\left(S_{+}\right)$。同理，可证 $f(x)\le 0,x\in \mathrm{conv}\left(S_{-}\right)$。则可以找到一个超平面将两个互不相交的凸壳分隔开。
3. 上述超平面可以将凸壳分隔开，则样本集满足线性可分
根据凸壳定义，数据集 $T$ 中正例点 $s_{+}\in \mathrm{conv}\left(S_{+}\right)，$ 负例点 $s_{-}\in \mathrm{conv}\left(S_{-}\right)$。上述超平面可以将正例点集 $S_{+}$和负例点集 $S_{-}$两个凸壳分隔开，则可以使样本集线性可分。充分性得证。

链接: DataWhale.