Leetcode面试经典150题-128.最长连续序列-递归版本另解
之前写过一篇这个题的,但是可能代码比较复杂,这回来个简洁版的,这个是递归版本
可以看看之前的版本,两个版本面试用哪个都保过
解法都在代码里,不懂就留言或者私信
class Solution {/**对于之前的解法,我现在提供一共更优的解,但是这种可能会比较难懂一些(思想方面)代码其实是很简洁的,总体思想如下:不需要排序直接把所有数放入map,map的key是当前数字,value是当前数开始的连续的长度初始值都是1,后面再遍历数组,遍历过程中查找当前数+1在map中的记录,直到找不到为止,比如我们第一个示例[100,4,200,1,3,2]我们便利到1的时候会在map中找到2的记录,然后取它的value+1,找2的过程又会递归查找3,直到找不到5的时候停,5的value是0,4取0+1=13取1+1=2 2取2+1=3,1取3+1=4而对于100,我们查找101就直接失败了,所以以它连续的就是0+1=1*/public int longestConsecutive(int[] nums) {/**如果长度小于2,有多少数就有多大的连续长度*/if(nums.length < 2) {return nums.length;}/**大于等于2的情况我们先把每个数都放在map里,key是数字本身,value是以它为开始的连续长度,初始值都设置为1这样做还有另外一个原因就是可以避免重复项的干扰*/Map<Integer, Integer> countMap = new HashMap<>();for(int num : nums) {countMap.put(num, 1);}/**定义结果值,既然有数,至少也得是个1吧*/int longest = 1;/**遍历数组,计算以当前数字开始的最长的长度*/for(int num : nums) {int curAns = countConsecutive(countMap, num);longest = Math.max(longest, curAns);}return longest;}/**通过countMap查找target开始的连续数字的长度 */public int countConsecutive(Map<Integer, Integer> countMap, int target) {/**我们通过主方法调用这个方法的时候当然target肯定是存在的,但是我们会递归调用 target+1直到不存在为止,所以这里一定要判断是不是存在,不存在返回0 */if(!countMap.containsKey(target)) {return 0;}/**这里有个大的优化,一定要做,如果当前map中存的target对应的value已经大于1了,说明算过了,不用重复计算不然每次都得从头开始一个一个算,肯定会超时的,比如先找1,然后找2.。。一直找到10000肯定不行,如果之前已经有2的记录了(大于1)现在取2的记录+1就行了 */if(countMap.get(target) > 1) {return countMap.get(target);}/**如果存在,找target+1开头的最大长度 */int count = countConsecutive(countMap, target + 1) + 1;/**不要忘了记录当前的结果*/countMap.put(target, count);return count;}
}运行时间和百分百确实有所提升,但是真的是同样的时间复杂度,也没感觉常数时间降低了多少

相关文章:

Leetcode面试经典150题-128.最长连续序列-递归版本另解
之前写过一篇这个题的,但是可能代码比较复杂,这回来个简洁版的,这个是递归版本 可以看看之前的版本,两个版本面试用哪个都保过 解法都在代码里,不懂就留言或者私信 class Solution {/**对于之前的解法,我…...

spring security 中的授权使用
一、认证 身份认证,就是判断一个用户是否为合法用户的处理过程。Spring Security 中支持多种不同方式的认证,但是无论开发者使用那种方式认证,都不会影响授权功能使用。因为 SpringSecurity 很好做到了认证和授权解耦。 二、授权 授权&#x…...
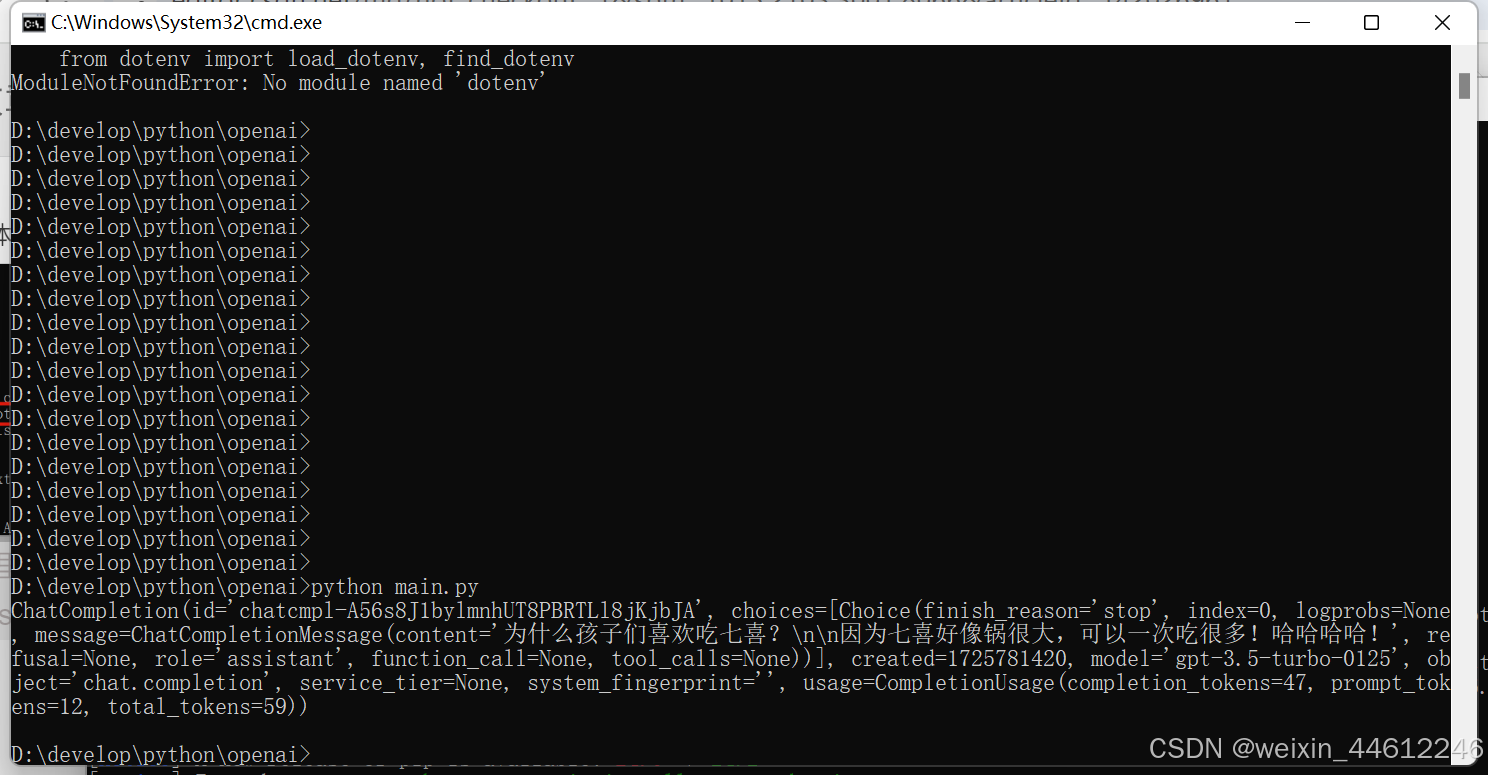
python安装以及访问openAI API
安装python 我是python小白,所以需要一步一步来,先安装。 一口吃不成胖子,记住。 从官网下载python,目前最新版本是3.12,但是据说稳定版3.11更好一点,所以,下载3.11,注意不要下载…...

【Unity小技巧】URP管线遮挡高亮效果
前言 在URP渲染管线环境下实现物体遮挡高亮显示效果,效果如下:Unity URP遮挡高亮 实现步骤 创建层级,为需要显示高亮效果的物体添加层级,比如Player 创建一个材质球,也就是高亮效果显示的材质球找到Universal Render…...
图形设备接口)
C#中的GDI和GDI+(Graphics Device Interface Plus)图形设备接口
GDI的概念 GDI(Graphics Device Interface)是微软Windows操作系统中的一个组件,它提供了一组API,用于在显示器或打印机等图形设备上进行图形绘制和图像处理。GDI 是 Windows 编程中用于二维图形和图像处理的接口。 GDI 的主要功…...

谷粒商城のNginx
文章目录 前言一、Nginx1、安装Nginx2、相关配置2.1、配置host2.2、配置Nginx2.3、配置网关 前言 本篇重点介绍项目中的Nginx配置。 一、Nginx 1、安装Nginx 首先需要在本地虚拟机执行: mkdir -p /mydata/nginx/html /mydata/nginx/logs /mydata/nginx/conf在项目…...

Debug-027-el-tooltip组件的使用及注意事项
前言: 这两天,碰到这个饿了么的el-tooltip比较多。这个组件使用起来也挺简单的,常用于展示鼠标 hover 时的提示信息。但是有一些小点需要注意。这里不再机械化的介绍文档,不熟悉的话可以先看一下: https://element-pl…...

猫眼电影字体破解(图片转码方法)
问题 随便拿一篇电影做样例。我们发现猫眼的页面数据在预览窗口中全是小方框。在当我们拿到源码以后,数据全是加密后的。所以我们需要想办法破解加密,拿到数据。 破解过程 1.源码获取问题与破解 分析 在我们刚刚请求url的时候是可以得到数据的ÿ…...

flink wordcount
Maven配置pom文件 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/P…...
)
组合模式(Composite Pattern)
使用组合模式(Composite Pattern)是一个更优雅的方式来表示菜单和菜单项。组合模式允许我们将单个对象(如菜单项)和组合对象(如菜单)以相同的方式处理。 解决方案: 创建组合结构:我…...
教你制作一本加密的样本册
在这个信息的时代,保护自己的隐私和知识产权变得尤为重要。你有没有想过,如何将自己珍贵的样本资料变成一本只有自己才能查看的加密宝典?今天,我就来教你制作一本加密的样本册 第一步,打开浏览器,搜索FLBOO…...

C语言进阶【1】--字符函数和字符串函数【1】
本章概述 字符分类函数字符转换函数strlen的使用和模拟实现strcpy的使用和模拟实现strcat的使用和模拟实现strcmp的使用和模拟实现彩蛋时刻!!! 字符分类函数 字符: 这个概念,我们在以前的文章中讲过了。我们键盘输入的…...

git提交自动带上 Signed-off-by信息
为了确保在使用 Signed-off-by 签名的同时保留你的提交消息,你需要修改 prepare-commit-msg 钩子脚本,以便它不会丢失原始的提交信息。 增加prepare-commit-msg 钩子以保留提交消息 prepare-commit-msg 钩子的目的是在提交信息文件中插入额外的内容&am…...

图论(2)
一、度 度统计的是一个节点上又多少条边 度出度入度 出度:统计以该节点为起始点箭头指向外面的边的条数 入度:统计箭头指向该节点的边数 度为1的节点为悬挂节点,边为悬挂边 用矩阵计算节点的度 二、握手定理 比如这里第一个集合里面有三…...

ASP.NET Core 入门教学十九 依赖注入ioc
ASP.NET Core内置了对依赖注入(Dependency Injection,简称DI)的支持,这是一种设计模式,用于实现控制反转(Inversion of Control,简称IoC),从而使得应用程序组件之间的耦合…...

omm kill 内存碎片化
内存频繁 OOM(Out of Memory)会导致内存碎片化,并进一步加剧无可用内存分配的问题。碎片化是内存管理中常见的问题,当系统频繁分配和释放内存时,内存空间会被分割成许多小块,虽然内存总量可能足够,但这些小块无法满足较大进程或数据的内存需求,最终导致系统无法找到足够…...
)
JS中给元素添加事件监听器的各种方法详解(包含比较和应用场景)
JavaScript 中给元素添加事件监听器的各种方法详解 在 JavaScript 中,事件处理是前端开发的一个重要部分。无论是点击按钮、提交表单,还是鼠标悬停,都涉及到事件监听。本文中,我将详细讲解各种给元素添加事件监听器的方法&#x…...

Python基本数据类型之复数complex
来源: “码农不会写诗”公众号 链接:Python基本数据类型之复数complex 文章目录 01 基本概念02 基本运算03 拓展1复数与向量 复数complex Python基本数据之复数(complex)即包含实部和虚部的数字。 01 基本概念 即包含实部和虚部的数字。 在Python中&am…...

第六届机器人与智能制造技术国际会议 (ISRIMT 2024)
目录 会议详情 主题 会议官网 会议详情 第六届机器人与智能制造技术国际研讨会(ISRIMT 2024)计划于2024年9月20-22日在常州举行。会议主要聚焦“机器人”和“智能制造技术”的研究领域,旨在为机器人和智能制造技术领域的专家学者、工程技术…...

鸿蒙轻内核M核源码分析系列十九 Musl LibC
往期知识点记录: 鸿蒙(HarmonyOS)应用层开发(北向)知识点汇总 轻内核M核源码分析系列一 数据结构-双向循环链表 轻内核M核源码分析系列二 数据结构-任务就绪队列 鸿蒙轻内核M核源码分析系列三 数据结构-任务排序链表 轻…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
