粒子群算法原理的示例介绍
一:粒子群优化算法的介绍
粒子群优化算法(PSO)是一种基于群体智能的优化算法,于1995年提出。它受到鸟群狩猎行为的启发,通过模拟鸟群或鱼群的社会行为来进行问题的求解。
基本原理
粒子群算法中,每个解决问题的潜在解被视为搜索空间中的一个“粒子”,每个粒子代表了问题的一个可能解。粒子在搜索空间中飞行,通过跟踪两个“极值”来更新自己的位置和速度:
1. 个体极值:粒子自身所经历的最优位置。
2. 全局极值:整个粒子群中所有粒子所经历的最优位置。
算法步骤
1. 初始化:随机初始化一群粒子的位置和速度。
2. 评价:计算每个粒子的适应度值。在粒子群优化算法(PSO)中,适应度值是用来评估粒子当前位置好坏的指标,它直接关系到粒子搜索最优解的能力。适应度函数(Fitness Function)是定义在搜索空间上的一个函数,它将粒子的位置映射到一个实数值,这个值越小(或越大,取决于优化问题的目标)表示粒子越优。
3. 更新个体极值:如果当前粒子的位置比它之前经历的最优位置更优,则更新个体极值。
4. 更新全局极值:如果当前粒子的位置比群体中所有粒子经历的最优位置更优,则更新全局极值。
5. 更新速度和位置:根据个体极值和全局极值更新每个粒子的速度和位置。
6. 迭代:重复步骤2-5,直到满足停止条件(如达到最大迭代次数或解的质量满足要求)。
算法公式
粒子的速度和位置更新公式通常如下:

二:粒子群优化算法的实现原理示例
实例:求解函数的最小值
目标函数:选择一个简单的多维函数,例如,我们的目标是找到这个函数的全局最小值。
1:导入必要的库
import numpy as np
这里导入了NumPy库,可用于大型多维数组的运算。
2:定义目标函数
def objective_function(position):x, y = positionreturn x**2 + y**2
3:初始化粒子群
def initialize_particles(n_particles, dim):particles = np.random.rand(n_particles, dim) * 20 - 10 # 在[-10, 10]范围内随机初始化velocities = np.zeros((n_particles, dim))return particles, velocities
这个函数初始化粒子群:
particles:一个二维数组,表示每个粒子的位置。位置是在 [−10,10][−10,10] 范围内随机初始化的。velocities:一个与particles大小相同的二维数组,表示每个粒子的速度。初始时,所有粒子的速度都是0。
4. 更新粒子速度和位置
def update_particles(particles, velocities, best_particle, best_global_position, c1=1.5, c2=1.5, w=0.5):for i in range(particles.shape[0]):r1, r2 = np.random.rand(2)velocities[i] = w * velocities[i] + c1 * r1 * (best_particle[i] - particles[i]) + c2 * r2 * (best_global_position - particles[i])particles[i] += velocities[i]
这个函数根据上述的速度和位置更新公式来更新粒子的速度和位置。
5. 粒子群优化主函数
def particle_swarm_optimization(n_particles, dim, max_iter, target_fitness):particles, velocities = initialize_particles(n_particles, dim)best_particle = particles.copy()best_global_position = particles[np.argmin([objective_function(p) for p in particles])]best_global_fitness = objective_function(best_global_position)for _ in range(max_iter):for i in range(particles.shape[0]):fitness = objective_function(particles[i])if fitness < objective_function(best_particle[i]):best_particle[i] = particles[i]if fitness < best_global_fitness:best_global_fitness = fitnessbest_global_position = particles[i]if best_global_fitness < target_fitness:breakupdate_particles(particles, velocities, best_particle, best_global_position)return best_global_position, best_global_fitness
这是PSO算法的主函数:
def particle_swarm_optimization(n_particles, dim, max_iter, target_fitness):
这个函数接受以下参数:
n_particles:粒子群中粒子的数量。dim:搜索空间的维度(在这个例子中是2维)。max_iter:算法执行的最大迭代次数。target_fitness:目标适应度值,当全局最优适应度小于这个值时,算法停止。
particles, velocities = initialize_particles(n_particles, dim)
这里调用
initialize_particles函数来初始化粒子群的位置和速度。
best_particle = particles.copy()
best_global_position = particles[np.argmin([objective_function(p) for p in particles])]
best_global_fitness = objective_function(best_global_position)
best_particle:每个粒子到目前为止找到的最好位置,初始时与粒子当前位置相同。best_global_position:整个群体到目前为止找到的最好位置,初始时是particles中适应度最小的位置。 NumPy函数np.argmin用于找到列表中的最小值的索引。在这里,它返回的是具有最小目标函数值的粒子的索引。best_global_fitness:全局最优适应度,即best_global_position处的适应度值。
for _ in range(max_iter):
这个主循环将在
max_iter指定的迭代次数内运行。
for i in range(particles.shape[0]):fitness = objective_function(particles[i])if fitness < objective_function(best_particle[i]):best_particle[i] = particles[i]if fitness < best_global_fitness:best_global_fitness = fitnessbest_global_position = particles[i]
对于每个粒子:
- 计算其当前适应度
fitness。- 如果当前适应度小于该粒子迄今为止找到的最好位置的适应度,则更新该粒子的最佳位置
best_particle[i]。- 如果当前适应度也小于全局最优适应度,则更新全局最优位置
best_global_position和全局最优适应度best_global_fitness。
if best_global_fitness < target_fitness:break
如果在任何时刻全局最优适应度小于目标适应度
target_fitness,则提前终止算法。我们在本示例中目标适应度target_fitness设为1e-6。
update_particles(particles, velocities, best_particle, best_global_position)
调用
update_particles函数来根据PSO的规则更新粒子的速度和位置。
return best_global_position, best_global_fitness
函数最后返回全局最优位置
best_global_position和全局最优适应度best_global_fitness。
整个算法的目标是找到目标函数 objective_function 的最小值,通过迭代地更新粒子的位置和速度,算法逐渐接近最优解。
6. 运行PSO算法
n_particles = 30
dim = 2
max_iter = 1000
target_fitness = 1e-6
best_position, best_fitness = particle_swarm_optimization(n_particles, dim, max_iter, target_fitness)
best_position, best_fitness
这里设置了PSO算法的参数并运行它。最后,打印出找到的最佳位置和适应度。这个实现的目标是找到使目标函数最小的 𝑥 和 𝑦。运行结果如下:
![]()
通过粒子群算法,我们成功找到了目标函数近似全局最小值。最终结果是在大约1000次迭代后得到的,最优位置接近于 (0, 0),这是函数的理论最小值点。最优适应度(即函数值)非常接近于0,这表明算法效果良好。
三:基于pyswarm库实现粒子群优化算法
pyswarm库中的粒子群优化(Particle Swarm Optimization,简称PSO)算法可以用来寻找一个目标函数的最优解,同时满足约束条件。接下来仍然为例,目标是找到这个函数的全局最小值。且pso函数默认寻找最小值。
-
导入pyswarm库中的pso函数
from pyswarm import pso这行代码导入了
pyswarm库中的pso函数,该函数是实现粒子群优化算法的核心。 -
定义目标函数
def objective_function(x):return x[0]**2 + x[1]**2这里定义了一个接受一个参数
x的函数,x是一个包含两个元素的列表或数组,分别代表两个决策变量。目标函数计算的是这两个决策变量的平方和。 -
定义约束条件
def constraint(x):return 1 - x[0]**2 - x[1]**2约束条件函数接受决策变量
x作为输入,并返回一个值。对于不等式约束,如果返回值大于等于0,则认为约束被满足。在这个例子中,约束条件意味着决策变量x的解必须在单位圆内。 -
使用pso函数进行优化
xopt, fopt = pso(objective_function, [-10, -10], [10, 10], f_ieqcons=constraint)这行代码调用了
pso函数来执行优化。以下是参数的说明:objective_function:前面定义的目标函数。[-10, -10]:决策变量的下界,表示每个变量可以取的最小值。[10, 10]:决策变量的上界,表示每个变量可以取的最大值。f_ieqcons=constraint:不等式约束条件。这里传递的是前面定义的constraint函数。
-
输出最优解和最优值:
print("最优解:", xopt) print("最优值:", fopt)这两行代码打印出优化算法找到的最优解
xopt(决策变量的值)和最优值fopt(目标函数在最优解处的值)。结果如下:
![]()
想要探索更多元化的数据分析视角,可以关注之前发布的相关内容。
相关文章:

粒子群算法原理的示例介绍
一:粒子群优化算法的介绍 粒子群优化算法(PSO)是一种基于群体智能的优化算法,于1995年提出。它受到鸟群狩猎行为的启发,通过模拟鸟群或鱼群的社会行为来进行问题的求解。 基本原理 粒子群算法中,每个解决…...

GNU/Linux - Open函数使用的O_CLOEXEC flag
在 Linux 中,“O_CLOEXEC ”标志与 “open ”系统调用一起使用,用于指定在使用 “exec ”系列函数(如 “execve”、“execl ”等)执行新程序时,“open ”返回的文件描述符应自动关闭。 In Linux, the O_CLOEXEC flag i…...

AWQ量化(Activation-aware Weight Quantization)
论文: AWQ: Activation-aware Weight Quantization for On-Device LLM Compression and Acceleration 中文解读: 深入理解AWQ量化技术 - 知乎 (zhihu.com) 动机:端侧设备用LLM,为了减少显存占用量,所以要用INT4量化&am…...

SprinBoot+Vue体育商品推荐的设计与实现
目录 1 项目介绍2 项目截图3 核心代码3.1 Controller3.2 Service3.3 Dao3.4 application.yml3.5 SpringbootApplication3.5 Vue 4 数据库表设计5 文档参考6 计算机毕设选题推荐7 源码获取 1 项目介绍 博主个人介绍:CSDN认证博客专家,CSDN平台Java领域优质…...

【Python基础】Python函数
本文收录于 《Python编程入门》专栏,从零基础开始,分享一些Python编程基础知识,欢迎关注,谢谢! 文章目录 一、前言二、函数的定义与调用三、函数参数3.1 位置参数3.2 默认参数3.3 可变数量参数(或不定长参数…...

【超简单】1分钟解决ppt全文字体一键设置
省流 ppt的全部字体需要在“幻灯片母版”里面,“自定义字体”去设置好标题与正文的字体之后才算全部设置完毕 “视图”---“幻灯片母版” 找到“字体”---“自定义字体” 设置好中文和西文的字体,都可以按照自己的选择来,保存即可 吐槽 之…...

数组与贪心算法——179、56、57、228(2简2中)
179. 最大数(简单) 给定一组非负整数 nums,重新排列每个数的顺序(每个数不可拆分)使之组成一个最大的整数。 注意:输出结果可能非常大,所以你需要返回一个字符串而不是整数。 解法一、自定义比较…...

WireShark过滤器
文章目录 一、WireShark过滤器概念1. 捕获过滤器(Capture Filters)2. 显示过滤器(Display Filters)3. 捕获过滤器与显示过滤器的区别4. 过滤器语法结构实际应用场景 二、WireShark捕获数据包列表1. **No.(序号…...

2024年全新deepfacelive如何对应使用直播伴侣-腾讯会议等第三方软件
# 2024年全新deepfacelive如何对应使用直播伴侣-腾讯会议等第三方软件 前提按照之前的步骤打开deepfacelive正确配置并且在窗口已经输出了换脸后的视频,不懂步骤可以移步 https://doc.youyacao.com/88/2225 ## 首先下载obs并配置 https://obsproject.com/ 通过…...

告别懵逼——前端项目调试与问题排查方法小结
在日常工作中,我们常常会遇到以下两类典型的挑战: 场景一: 接手无文档的老项目 1、情景描述: 你接手了一个历史久远的项目,项目文档缺失,前任开发者已经离开,而你对当前的业务逻辑和代码结构都…...

[数据集][目标检测]肺炎检测数据集VOC+YOLO格式4983张2类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):4983 标注数量(xml文件个数):4983 标注数量(txt文件个数):4983 标注…...

顶层const和底层const
在C中,const修饰符用于声明常量,有两种常见的形式:顶层const和底层const,它们之间的区别在于它们修饰的对象及其在不同场景中的作用。 1. 顶层const (Top-level const) 顶层const用于修饰变量本身,使其成为常量。这意…...

嵌入式Openharmony系统构建与启动详解
大家好,今天主要给大家分享一下,如何构建Openharmony子系统以及系统的启动过程分解。 第一:OpenHarmony系统构建 首先熟悉一下,构建系统是一种自动化处理工具的集合,通过将源代码文件进行一系列处理,最终生成和用户可以使用的目标文件。这里的目标文件包括静态链接库文件…...

锡林郭勒奶酪品牌呼和浩特市大召店盛大开业
礼献中秋,香飘乳都。为进一步拓展锡林郭勒奶酪区域公用品牌产品销售渠道,9月8日,锡林郭勒奶酪区域公用品牌大召店在呼和浩特市大召广场月明楼隆重开业,现场为第三批新授权的39家奶酪生产经营主体代表授牌。至此,锡林郭…...

【Java算法】模拟
🔥个人主页: 中草药 🔥专栏:【算法工作坊】算法实战揭秘 🧣 一.模拟算法 模拟算法和传统的算法有一些不同之处,更多的是对题目要求的理解,通过代码的方式去模拟实现一道题目在现实中的实现方法…...
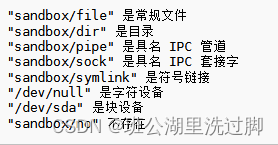
标准库标头 <filesystem> (C++17)学习之文件类型
本篇介绍filesystem文件库的文件类型API。 文件类型 is_block_file (C17) 检查给定的路径是否表示块设备 (函数) is_character_file (C17) 检查给定的路径是否表示字符设备 (函数) is_directory (C17) 检查给定的路径是否表示一个目录 (函数) is_empty (C17) 检查给定的路径是…...

基于51单片机的自动转向修复系统的设计与实现
文章目录 前言资料获取设计介绍功能介绍设计清单具体实现截图参考文献设计获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师,一名热衷于单片机技术探索与分享的博主、专注于 精通51/STM32/MSP430/AVR等单片机设…...

mysql笔记4(数据类型)
数据库的数据类型应该是数据库架构师(DBA)和产品经理沟通后依据公司的项目、业务而定的,而且会不停地变化。数据类型的选择方面没有一个统一的标准,但是应该符合业务、项目的逻辑标准。 菜鸟教程 Mysql 数据类型 文章目录 1. int类型2. 浮点数3. 定点数4…...
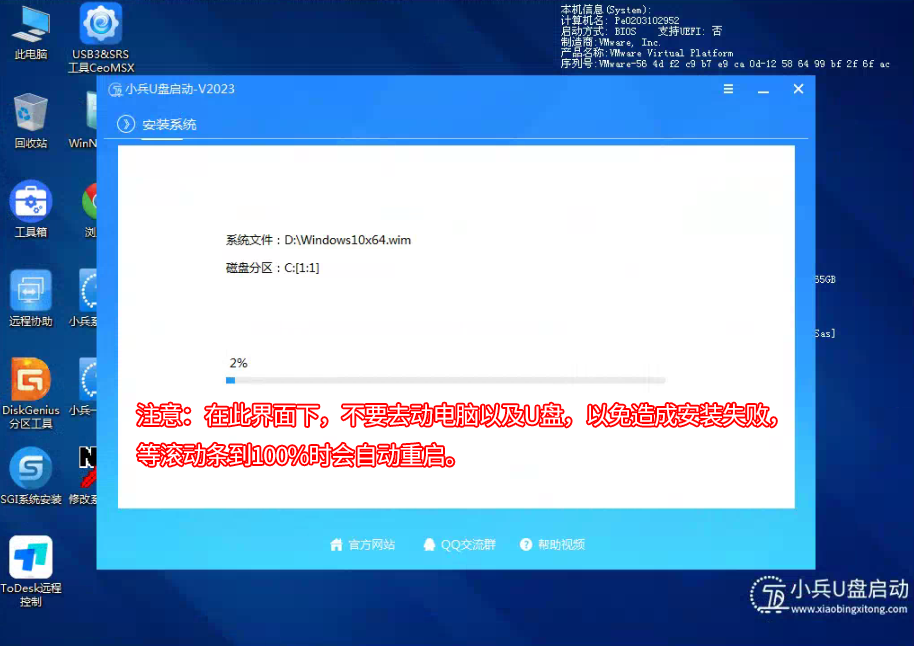
电脑开机出现no operation system found错误原因分析及解决方法
最近有网友问我电脑一启动提示:no operation system found,这个提示意思是未找到操作系统。并且出现bios能认别硬盘,快捷启动时找不到硬盘,出现该提示的原因有很多,下面我们来详细分析一下开机出现no operation system…...
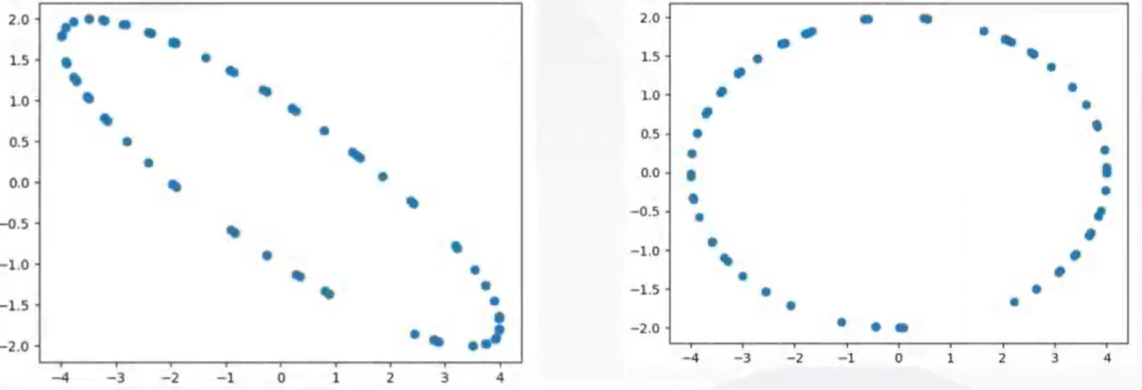
数学建模笔记—— 主成分分析(PCA)
数学建模笔记—— 主成分分析 主成分分析1. 基本原理1.1 主成分分析方法1.2 数据降维1.3 主成分分析原理1.4 主成分分析思想 2. PCA的计算步骤3. 典型例题4. 主成分分析说明5. python代码实现 主成分分析 1. 基本原理 在实际问题研究中,多变量问题是经常会遇到的。变量太多,无…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...
