数学建模笔记—— 主成分分析（PCA)

主成分分析

1. 基本原理

在实际问题研究中,多变量问题是经常会遇到的。变量太多,无疑会增加分析问题的难度与复杂性,而且在许多实际问题中,多个变量之间是具有一定的相关关系的。因此,人们会很自然地想到,能否在相关分析的基础上,用较少的新变量代替原来较多的旧变量,而且使这些较少的新变量尽可能多地保留原来变量所反映的信息?

一个简单的例子：

例如,某人要做一件上衣要测量很多尺寸,如身长、袖长、胸围、腰围、肩宽、肩厚等十几项指标,但某服装厂要生产一批新型服装绝不可能把尺寸的型号分得过多?

我们可以把多种指标中综合成几个少数的综合指标,做为分类的型号,将十几项指标综合成3项指标,一项是反映长度的指标,一项是反映胖瘦的指标,一项是反映特殊体型的指标。

1.1 主成分分析方法

在分析研究多变量的课题时,变量太多就会增加课题的复杂性。人们自然希望变量个数较少而得到的信息较多。在很多情形,变量之间是有一定的相关关系的,可以解释为这两个变量反映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量,将重复的变量(关系紧密的变量)删去多余,建立尽可能少的新变量,使得这些新变量是两两不相关的,且这些新变量在反映课题的信息方面尽可能保持原有的信息。设法将原来变量重新组合成一组新的互相无关的几个综合变量,同时根据实际需要从中可以取出几个较少的综合变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析,也是数学上用来降维的一种方法。

1.2 数据降维

降维是将高维度的数据(指标太多)保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的。在实际的生产和应用中,降维在一定的信息损失范围内,可以为我们节省大量的时间和成本。降维也成为应用非常广泛的数据预处理方法。

降维优点：

1. 使得数据集更易使用
2. 除噪声
3. 降低算法的计算开销
4. 使得结果容易理解

1.3 主成分分析原理

PCA的主要目标是将特征维度变小,同时尽量减少信息损失。就是对一个样本矩阵,**一是换特征,**找一组新的特征来重新标识;**二是减少特征,**新特征的数目要远小于原特征的数目。

通过PCA将n维原始特征映射到k维(k<n)上,称这k维特征为主成分。需要强调的是,不是简单地从n维特征中去除其余n-k维特征,而是重新构造出全新的k维正交特征,且新生成的k维数据尽可能多地包含原来n维数据的信息。例如,使用PCA将20个相关的特征转化为5个无关的新特征,并且尽可能保留原始数据集的信息。

怎么找到新的维度呢?实质是数据间的方差够大,通俗地说,就是能够使数据到了新的维度基变换下,坐标点足够分散,数据间各有区分。

如图所示的左图中有5个离散点,降低维度,就是需要把点映射成一条线。将其映射到右图中黑色虚线上则样本变化最大,且坐标点更分散,这
条黑色虚线就是第一主成分的投影方向。

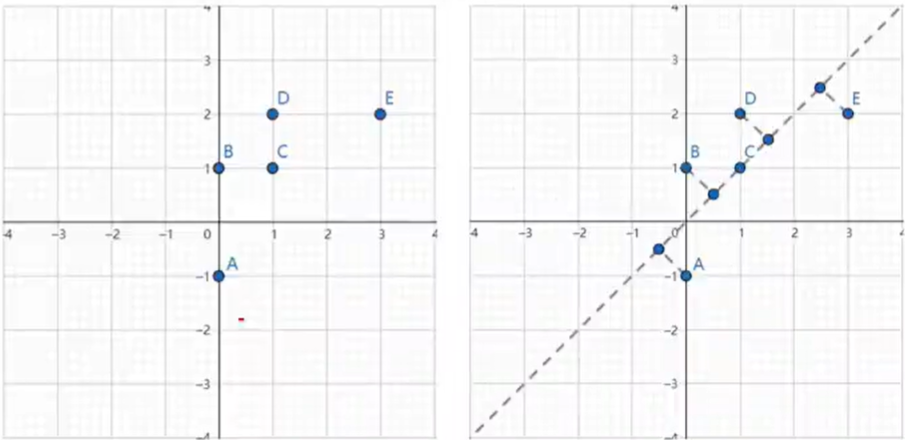
PCA是一种线性降维方法,即通过某个投影矩阵将高维空间中的原始样本点线性投影到低维空间,以达到降维的目的,线性投影就是通过矩阵变换的方式把数据映射到最合适的方向。

降维的几何意义可以理解为旋转坐标系,取前k个轴作为新特征。

对于下图所示的情况，我们发现这些数据都几乎排列在一条直线上，并且在x轴方向和y轴方向的方差都比较大。但是如果把坐标轴旋转一定角度，使得这些数据在某个坐标轴的投影的方差比较大，便可以用新坐标系下方差较大的一个坐标轴坐标作为主成分。对于左图，数据为(1,2)、(2,4)…旋转坐标轴后，坐标为$(\sqrt{5},0)、\left(\begin{array}{c}2\sqrt{5},1\end{array}\right)\dots \dots$这样主成分就是新坐标系下变量$x$的数值$\sqrt{5}、2\sqrt{5}......$

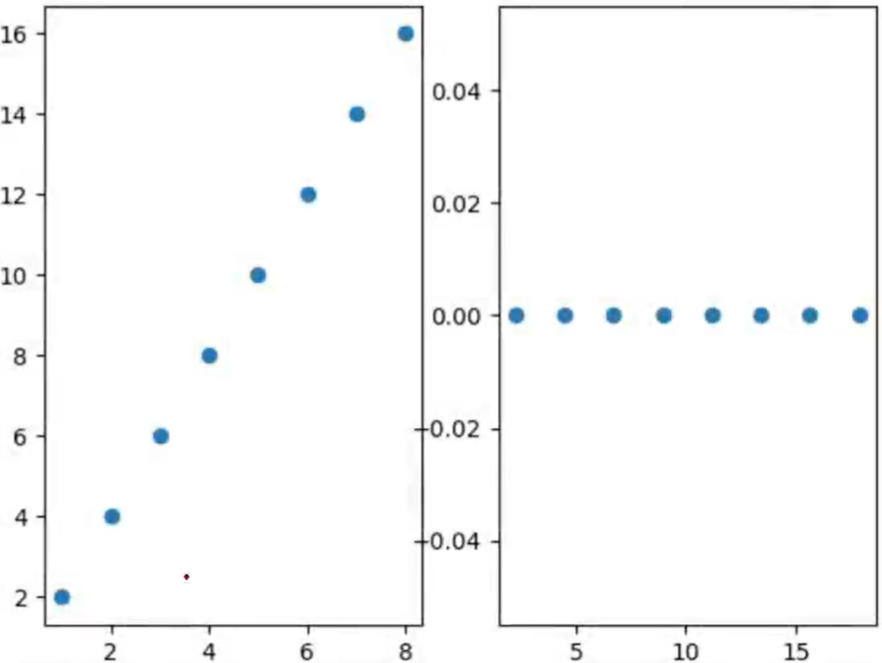
对于大多数情况,数据各个变量基本服从正态分布,所以变量为2的数据散点分布大致为一个椭圆,变量为3的散点分布大致为一个椭球,p个变量的数据大致分布在一个超椭圆。而通过旋转坐标系,使得超椭圆的长轴落在一个坐标轴上,其次超椭圆另一个轴也尽量落在坐标轴上。这样各个新的坐标轴上的坐标值便是相应的主成分。

例如,对于图示的数据,在x轴和y轴的方差都很大,所以可以旋转坐标系,使得椭圆两个轴尽量落在坐标轴上。这样,我们便以散点在新坐标系下的x坐标作为第一主成分(因为x方向方差最大),y轴的坐标为第二主成分。

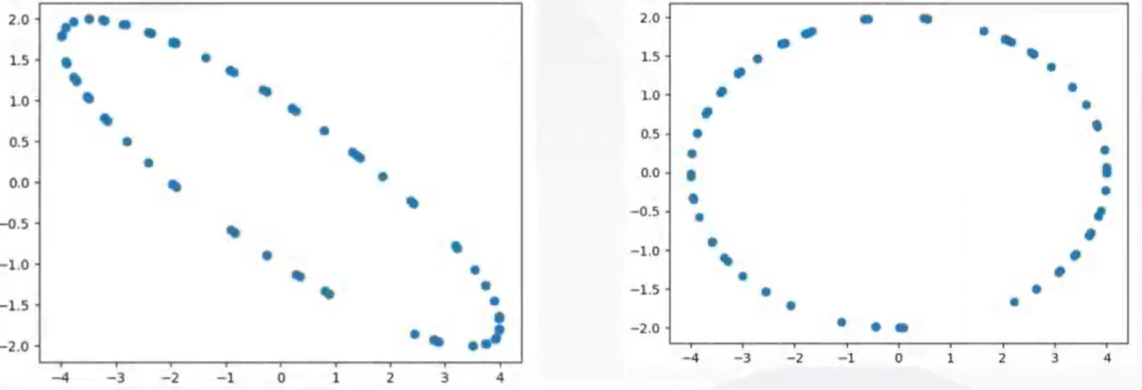
主成分分析的理论推导较为复杂,需要借助投影寻踪,构造目标函数等方法来推导,在多元统计的相关书籍中都有详细讲解。但是其结论却是十分简洁。所以,如果只是需要实际应用,了解主成分分析的基本原理与实现方法便足够了。

降维的代数意义可以理解为：

$m\times n$阶的原始样本$X$，与$n\times k$阶矩阵$W$做矩阵乘法运算$X\times W$，即可得到$m\times k$阶低维矩阵$Y$，这里的$n\times k$阶矩阵$W$就是投影矩阵。

1.4 主成分分析思想

假设有$n$个样本，$p$个指标，则可构成大小为$n\times p$的样本矩阵$x:$
$$x=\left[\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1p}\\ x_{21}& x_{22}& \cdots & x_{2p}\\ ⋮& ⋮& \ddots & ⋮\\ x_{n1}& x_{n2}& \cdots & x_{np}\end{array}\right]=\left(\begin{array}{c}{x}_1,x_2,\cdots ,x_p\end{array}\right)$$
假设我们想找到新的一组变量$z_1,z_2,\cdot \cdot \cdot ,z_m(m\le p)$，且它们满足：
$$\{\begin{array}{l}{z}_1=l_{11}{x}_1+l_{12}{x}_2+\cdots +l_{1p}{x}_p\\ z_2=l_{21}{x}_1+l_{22}{x}_2+\cdots +l_{2p}{x}_p\\ ⋮\\ z_m=l_{m1}{x}_1+l_{m2}{x}_2+\cdots +l_{mp}{x}_p\end{array}$$
系数$l_{ij}$的确定原则：

1. $z_i$与$z_j(i\ne j;i,j=1,2,,m)$相互无关
2. $z_1$是与$x_1,x_2,...,x_p$ 的一切线性组合中方差最大者
3. $z_2$与$z_1$不相关的$x_1,x_2,...,x_p$ 的一切线性组合中方差最大者
4. 以此类推，$z_m$是与$z_1,z_2,...,z_{m-1}$不相关的$x_1,x_2,...,x_p$ 的所有线性组合中方差最大者
5. 新变量指标$z_1,z_2,...,z_m$分别称为原变量指标$x_1,x_2,...,x_p$的第一，第二，…,第m主成分

2. PCA的计算步骤

假设有$n$个样本，$p$个指标，则可构成大小为$n\times p$的样本矩阵$x:$
$$x=\left[\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1p}\\ x_{21}& x_{22}& \cdots & x_{2p}\\ ⋮& ⋮& \ddots & ⋮\\ x_{n1}& x_{n2}& \cdots & x_{np}\end{array}\right]=\left(\begin{array}{c}{x}_1,x_2,\cdots ,x_p\end{array}\right)$$

1. 首先对其进行标准化处理

   按列计算均值${\overline{x}}_j=\frac{1}{n}{\Sigma }_{i=1}^n{x}_{ij}$和标准差$S_j=\sqrt{\frac{{\sum }_{i=1}^n(x_{ij}-\overline{x_j}{)}^2}{n-1}}$ , 计算得标准化数据$X_{ij}=\frac{x_{ij}-\overline{x_j}}{s_j}$
   原始样本矩阵经过标准化变为：
   $$\begin{array}{rl}& X=\left[\begin{array}{cccc}{X}_{11}& X_{12}& \cdots & X_{1p}\\ X_{21}& X_{22}& \cdots & X_{2p}\\ ⋮& ⋮& \ddots & ⋮\\ X_{n1}& X_{n2}& \cdots & X_{np}\end{array}\right]=\left(\begin{array}{c}{X}_1,X_2,\cdots ,X_p\end{array}\right)\end{array}$$

2. 计算标准化样本的协方差矩阵/样本相关系数矩阵
   $$\begin{array}{rl}& R=\left[\begin{array}{cccc}{r}_{11}& r_{12}& \cdots & r_{1p}\\ r_{21}& r_{22}& \cdots & r_{2p}\\ ⋮& ⋮& \ddots & ⋮\\ r_{n1}& r_{n2}& \cdots & r_{np}\end{array}\right]\\ & \text{其中}{r}_{ij}=\frac{1}{n-1}\sum _{k=1}^n(X_{ki}-\overline{X_i})(X_{kj}-\overline{X_j})\end{array}$$

3. 计算$R$的特征值和特征向量
   $$\begin{array}{rl}& \text{特征值:}{\lambda }_1\ge {\lambda }_2\ge ...\ge {\lambda }_p\ge 0\\ & \text{特征向量:}{a}_1=\left[\begin{array}{c}{a}_{11}\\ a_{21}\\ ⋮\\ a_{p1}\end{array}\right],a_2=\left[\begin{array}{c}{a}_{12}\\ a_{22}\\ ⋮\\ a_{p2}\end{array}\right],\cdots ,a_p=\left[\begin{array}{c}{a}_{1p}\\ a_{2p}\\ ⋮\\ a_{pp}\end{array}\right]\end{array}$$

4. 计算主成分贡献率以及累计贡献率
   $$\text{贡献率}{\alpha }_i\frac{{\lambda }_i}{{\sum }_{k=1}^p{\lambda }_k}(i=1,2,...,p)\text{累计贡献率}\sum G\frac{{\sum }_{k-1}^i{\lambda }_k}{{\sum }_{k=1}^p{\lambda }_k}(i=1,2,...,p)$$

5. 写出主成分

   一般取累计贡献率超过80%的特征值所对应的第一、第二、…第$m(m\le p)$个主成分。第$i$个主成分：
   $$F_i=a_{1i}{X}_1+a_{2i}{X}_2+...+a_{pi}{X}_p(i=1,2,...,m)$$

6. 根据系数分析主成分代表的意义

   对于某个主成分而言，指标前面的系数越大，代表该指标对于该主成分的影响越大。

7. 利用主成分的结果进行后续的分析

   • 主成分得分
   • 聚类分析
   • 回归分析

3. 典型例题

在制定服装标准的过程中，对128名成年男子的身材进行了测量，每人测得的指标中含有这样的六项：身高$(x_1)$、坐高$(x_2)$、胸围$(x_3)$、手臂长$(x_4)$、肋围$(x_5)$、腰围$(x_6)$。所得样本相关系数矩阵(对称矩阵)如下表：

	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$
$x_1$	1	0.79	0.36	0.76	0.25	0.51
$x_2$	0.79	1	0.31	0.55	0.17	0.35
$x_3$	0.36	0.31	1	0.35	0.64	0.58
$x_4$	0.76	0.55	0.35	1	0.16	0.38
$x_5$	0.25	0.17	0.64	0.16	1	0.63
$x_6$	0.51	0.35	0.58	0.38	0.63	1

注意：本题给我们的数据直接就是样本相关系数矩阵，一般来说，大家自己建模的时候，得到的是原始数据。

经过计算，相关系数矩阵的特征值、相应的特征向量以及贡献率列于下表：

特征向量	$a_1$	$a_2$	$a_3$	$a_4$	$a_5$	$a_6$
$x_1:$ 身高	0.469	-0.365	0.092	-0.122	-0.080	-0.786
$x_2:$ 坐高	0.404	-0.397	0.613	0.326	0.027	0.443
$x_3:$ 胸围	0.394	0.397	-0.279	0.656	0.405	-0.125
$x_4:$ 手臂长	0.408	-0.365	-0.705	-0.108	-0.235	0.371
$x_5:$ 肋围	0.337	0.569	0.164	-0.019	-0.731	0.034
$x_6:$ 腰围	0.427	0.308	0.119	-0.661	0.490	0.179
特征值	3.287	1.406	0.459	0.426	0.295	0.126
贡献率	0.548	0.234	0.077	0.071	0.049	0.021
累计贡献率	0.548	0.782	0.859	0.930	0.979	1.000

从表中可以看到前三个主成分的累计贡献率达85.9%,因此可以考虑只取三个主成分，他们能够很好地概括原始变量。

写出主成分并分析解释含义
$$\begin{gathered} F_1=0.469X_1+0.404X_2+0.394X_3+0.408X_4+0.339X_5+0.427X_6 \\ {F}_2=-0.365X_1-0.397X_2+0.397X_3-0.365X_4+0.569X_5+0.308X_6 \\ {F}_3=0.092X_1+0.613X_2-0.279X_3-0.705X_4+0.164X_5+0.119X_6 \\ {X}_i均是标准化后的指标，x_i:身高、坐高、胸围、手臂长、肋围和腰围 \end{gathered}$$

• 第一主成分$F_1$对所有(标准化)原始变量都有近似相等的正载荷，故称第一主成分为**(身材)大小成分**
• 第二主成分$F_2$在$X_3,X_5,X_6$上有中等程度的正载荷，而在$X_1,X_2,X_4$上有中等程度的负载荷，称第二主成分为形状成分(或胖瘦成分)
• 第三主成分$F_3$在$X_2$上有大的正载荷，在$X_4$上有大的负载荷，而在其余变量上的载荷都较小，可称为第三主成分为臂长成分
• 当然，由于第三主成分贡献率不算高，实际意义也不太重要，因此我们可以考虑只取前两个。

4. 主成分分析说明

在主成分分析中,我们首先应保证所提取的前几个主成分的累计贡献率达到一个较高的水平,其次对这些被提取的主成分必须都能够给出符合实际背景和意义的解释。

主成分的解释其含义一般多少带有点模糊性,不像原始变量的含义那么清楚、确切,这是变量降维过程中不得不付出的代价。因此,提取的主成分个数m通常应明显小于原始变量个数p(除非p本身较小),否则维数降低的“利”可能抵不过主成分含义不如原始变量清楚的“弊”。

如果原始变量之间具有较高的相关性,则前面少数几个主成分的累计贡献率通常就能达到一个较高水平,也就是说,此时的累计贡献率通常较易得到满足。主成分分析的困难之处主要在于要能够给出主成分的较好解释,所提取的主成分中如有一个主成分解释不了,整个主成分分析也就失败了。主成分分析是变量降维的一种重要、常用的方法,简单的说,该方法要应用得成功,一是靠原
始变量的合理选取,二是靠“运气”。

– 参考教材:《应用多元统计分析》王学民

5. python代码实现

数据data.csv内容如下：

年份,单产,种子费,化肥费,农药费,机械费,灌溉费
1990,1017.0,106.05,495.15,305.1,45.9,56.1
1991,1036.5,113.55,561.45,343.8,68.55,93.3
1992,792.0,104.55,584.85,414.0,73.2,104.55
1993,861.0,132.75,658.35,453.75,82.95,107.55
1994,901.5,174.3,904.05,625.05,114.0,152.1
1995,922.5,230.4,1248.75,834.45,143.85,176.4
1996,916.5,238.2,1361.55,720.75,165.15,194.25
1997,976.5,260.1,1337.4,727.65,201.9,291.75
1998,1024.5,270.6,1195.8,775.5,220.5,271.35
1999,1003.5,286.2,1171.8,610.95,195.0,284.55
2000,1069.5,282.9,1151.55,599.85,190.65,277.35
2001,1168.5,317.85,1105.8,553.8,211.05,290.1
2002,1228.5,319.65,1213.05,513.75,231.6,324.15
2003,1023.0,368.4,1274.1,567.45,239.85,331.8
2004,1144.5,466.2,1527.9,487.35,408.0,336.15
2005,1122.0,449.85,1703.25,555.15,402.3,358.8
2006,1276.5,537.0,1888.5,637.2,480.75,428.4
2007,1233.0,565.5,2009.85,715.65,562.05,456.9

源码如下：

import pandas as pd
import numpy as np# 在python中导入scipy库的linalg模块
# scipy是python中的一个科学计算库，linalg模块包含了线性代数的函数
from scipy import linalg# 读取csv文件的后五行
df = pd.read_csv('data.csv', usecols=[2, 3, 4, 5, 6])
# print(df)# df.to_numpy()是pandas对象中的一个方法，用于将DataFrame转换为NumPy数组
x = df.to_numpy()
# print(x)# 标准化数据
X = (x-np.mean(x, axis=0))/np.std(x, ddof=1, axis=0)# 计算协方差矩阵
R = np.cov(X.T)# 计算特征值和特征向量
eigvals, eigvecs = linalg.eigh(R)
# 将特征值数组按降序排列
eigvals = eigvals[::-1]
# 将特征向量数组按降序排列
eigvecs = eigvecs[:, ::-1]# 计算主成分贡献率和累积贡献率
contribution_rate = eigvals/sum(eigvals)
# np.cumsum()是numpy中的一个函数，用于计算数组的累积和
cumulative_contribution_rate = np.cumsum(contribution_rate)# 打印结果
print("特征值为：")
print(eigvals)
print("贡献率为：")
print(contribution_rate)
print("累积贡献率为：")
print(cumulative_contribution_rate)
print("与特征值对应的特征向量为：")
print(eigvecs)

输出结果：

特征值为：
[4.09453559 0.79266524 0.08165257 0.02069963 0.01044696]
贡献率为：
[0.81890712 0.15853305 0.01633051 0.00413993 0.00208939]
累积贡献率为：
[0.81890712 0.97744017 0.99377068 0.99791061 1.        ]
与特征值对应的特征向量为：
[[-0.48104689  0.23837363 -0.01782683 -0.0038534   0.84346859][-0.48753322 -0.07920883 -0.33594594 -0.7565078  -0.26622096][-0.28138862 -0.92242424 -0.00452323  0.24430868  0.10122639][-0.47315152  0.26834026 -0.46128305  0.60577733 -0.35266544][-0.47733984  0.11845256  0.82098722  0.03206562 -0.28821424]]