【Leetcode152】乘积最大子数组(动态规划)
文章目录
- 一、题目
- 二、思路
- 三、代码
一、题目

二、思路
(0)读懂题意:题目的“连续”是指位置的连续,而不是说数字的连续,这是个大坑。
(1)确定状态:定义两个状态来记录当前子数组的最大乘积、最小乘积。因为在处理负数时,最小乘积乘以负数可能变为最大乘积。dp_max[i]表示以nums[i]结尾的子数组的最大乘积、dp_min[i]表示以nums[i]结尾的子数组的最小乘积。
(2)状态转移方程:对于每个元素nums[i],我们的dp_max[i]和dp_min[i]可以从这三个数中确定:
- 只包含当前元素
nums[i]。 - 当前元素与之前的最大乘积子数组乘积,即
dp_max[i-1] * nums[i]。 - 当前元素与之前的最小乘积子数组乘积,即
dp_min[i-1] * nums[i]。
即状态转移方程可表示为:
dp_max[i] = max(nums[i], dp_max[i-1] * nums[i], dp_min[i-1] * nums[i])
dp_min[i] = min(nums[i], dp_max[i-1] * nums[i], dp_min[i-1] * nums[i])
(3)初始状态+边界条件:以第一个元素结尾的子数组最大乘积就是它本身、以第一个元素结尾的子数组最小乘积就是它本身、初始乘积最大结果为第一个元素。
(4)遍历顺序:从左到右遍历数组。
三、代码
(方法一)按照思路的代码如下,时间复杂度为O(n),空间复杂度为O(n)。
class Solution(object):def maxProduct(self, nums):""":type nums: List[int]:rtype: int"""if len(nums) == 0:return 0if len(nums) == 1:return nums[0]# 初始化数组n = len(nums)dp_max = [0] * n dp_min = [0] * n# 初始状态dp_max[0] = nums[0]dp_min[0] = nums[0]cheng_ans = nums[0]# 从第二个元素开始遍历for i in range(1, n):num = nums[i]dp_max[i] = max(num, dp_max[i-1]*num, dp_min[i-1]*num)dp_min[i] = min(num, dp_max[i-1]*num, dp_min[i-1]*num)cheng_ans = max(cheng_ans, dp_max[i])return cheng_ans
(方法二)为了优化空间复杂度,发现每次当前只利用前一次状态,所以dp_max和dp_min没必要单独用两个数组记录所有的状态。但注意在计算状态转移方程时,分别计算dp_max和dp_min都会用到上一次的dp_max和dp_min,这为了用错dp_mxn,可以直接对num确保是正数后,交换dp_max和dp_min的位置,减少max和min函数的入参个数。
class Solution(object):def maxProduct(self, nums):""":type nums: List[int]:rtype: int"""if len(nums) == 0:return 0if len(nums) == 1:return nums[0]# 初始化数组n = len(nums)# 初始状态dp_max = nums[0]dp_min = nums[0]cheng_ans = nums[0]# 从第二个元素开始遍历for i in range(1, n):num = nums[i]if num < 0:dp_max, dp_min = dp_min, dp_maxdp_max = max(num, dp_max*num)dp_min = min(num, dp_min*num)cheng_ans = max(cheng_ans, dp_max)return cheng_ans
相关文章:

【Leetcode152】乘积最大子数组(动态规划)
文章目录 一、题目二、思路三、代码 一、题目 二、思路 (0)读懂题意:题目的“连续”是指位置的连续,而不是说数字的连续,这是个大坑。 (1)确定状态:定义两个状态来记录当前子数组的…...

STM32(十二):DMA直接存储器存取
DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设和存储器或者存储器和存储器之间的高速数据传输,无须CPU干预,节省了CPU的资源。(运行内存SRAM、程序存储器Flash、寄存器) 12个独立可配置的通道&…...
的“炒股”经历和感受)
关于我2020年7月至今(2024.9)的“炒股”经历和感受
声明:我远不是一个成熟的投资者(这个名词太大了,我那三瓜两枣似乎完全配不上投资者这三个字,或者“小小散”更加贴切)。本文不构成任何入(股)市的引导或者买卖股票的建议。 “炒股”这个词,相信绝大多数人看来都-是一个贬义词&…...

【Tools】Prompt Engineering简介
摇来摇去摇碎点点的金黄 伸手牵来一片梦的霞光 南方的小巷推开多情的门窗 年轻和我们歌唱 摇来摇去摇着温柔的阳光 轻轻托起一件梦的衣裳 古老的都市每天都改变模样 🎵 方芳《摇太阳》 大模型中的Prompt Engineering是指为了提高大模型在特定任…...

多路转接之select(fd_set介绍,参数详细介绍),实现非阻塞式网络通信
目录 多路转接之select 引入 介绍 fd_set 函数原型 nfds readfds / writefds / exceptfds readfds 总结 fd_set操作接口 timeout timevalue 结构体 传入值 返回值 代码 注意点 -- 调用函数 select的参数填充 获取新连接 注意点 -- 通信时的调用函数 添…...

乐鑫安全制造全流程
主要参考资料: 【乐鑫全球开发者大会】DevCon24 #10 |乐鑫安全制造全流程 乐鑫官方文档Flash加密: https://docs.espressif.com/projects/esp-idf/zh_CN/latest/esp32/security/flash-encryption.html 【ESP32S3】使用 Flash 下载工具完成 Flash 加密功能…...

〖open-mmlab: MMDetection〗解析文件:configs/_base_/schedules
详细解析三个训练调度文件:schedule_1x.py、schedule_2x.py、schedule_20e.py 在深度学习模型训练过程中,训练调度(Training Schedule)是至关重要的,它决定了模型训练过程中学习率(Learning Rate, LR&…...

Android之Handler是如何保证延迟发送的
目录 核心组件延迟发送消息的工作原理具体步骤1. 创建 Handler:2.发送延迟消息3.消息入队列4.消息出队和处理: 关键点总结 在 Android 中,Handler 是用于在不同线程之间传递和处理消息的工具。它可以用于定时任务、延迟执行任务等。Handler 如何保证延迟发送消息的核…...

定位信标、基站、标签,定位信标是什么
定位信标、基站、标签,定位信标是什么 今天给各位分享定位信标、基站、标签的知识,其中也会对定位信标是什么进行解释,如果能碰巧解决你现在面临的问题,别忘了关注本站,现在开始吧! 怎样做人员定位啊? 〖…...

2024国赛数学建模B题完整分析参考论文38页(含模型和可运行代码)
2024 高教社杯全国大学生数学建模完整分析参考论文 B 题 生产过程中的决策问题 目录 摘要 一、问题重述 二、问题分析 三、 模型假设 四、 模型建立与求解 4.1问题1 4.1.1问题1思路分析 4.1.2问题1模型建立 4.1.3问题1样例代码(仅供参考) 4.…...

Hive是什么?
Apache Hive 是一个基于 Hadoop 的数据仓库工具,用于在 Hadoop 分布式文件系统(HDFS)上管理和查询大规模结构化数据集。Hive 提供了一个类似 SQL 的查询语言,称为 HiveQL,通过这种语言可以在 HDFS 上执行 MapReduce 作…...

计算机网络:http协议
计算机网络:http协议 一、本文内容与前置知识点1. 本文内容2. 前置知识点 二、HTTP协议工作简介1. 特点2. 传输时间分析3. http报文结构 三、HTTP版本迭代1. HTTP1.0和HTTP1.1主要区别2. HTTP1.1和HTTP2主要区别3. HTTPS与HTTP的主要区别 四、参考文献 一、本文内容…...

【stata】自写命令分享dynamic_est,一键生成dynamic effect
1. 命令简介 dynamic_est 是一个用于可视化动态效应(dynamic effect)的工具。它特别适用于事件研究(event study)或双重差分(Difference-in-Differences, DID)分析。通过一句命令即可展示动态效应…...

文心一言 VS 讯飞星火 VS chatgpt (342)-- 算法导论23.2 1题
一、对于同一个输入图,Kruskal算法返回的最小生成树可以不同。这种不同来源于对边进行排序时,对权重相同的边进行的不同处理。证明:对于图G的每棵最小生成树T,都存在一种办法来对G的边进行排序,使得Kruskal算法所返回的…...

部署若依Spring boot项目
nohup和& nohup命令解释 nohup命令:nohup 是 no hang up 的缩写,就是不挂断的意思,但没有后台运行,终端不能标准输入。 nohup :不挂断的运行,注意并没有后台运行的功能,就是指,用nohup运行命令可以使命令永久的执行下去,和用户终端没有关系,注意了nohup没有后台…...

oc打包:权限弹窗无法正常弹出
在遇到编写了权限无法弹出弹窗时,需要查看是不是调用时机不对,这里直接教万能改法。 将权限获取方法编写在applicationDidBecomeActive 进入前台的生命周期接口中,如下: if (@available(iOS 14, *)) {NSLog<...

深入理解RxJava:响应式编程的现代方式
在当今的软件开发世界中,异步编程和事件驱动的架构变得越来越重要。RxJava,作为响应式编程(Reactive Programming)的一个流行库,为Java和Android开发者提供了一种强大的方式来处理异步任务和事件流。本文将深入探讨RxJ…...
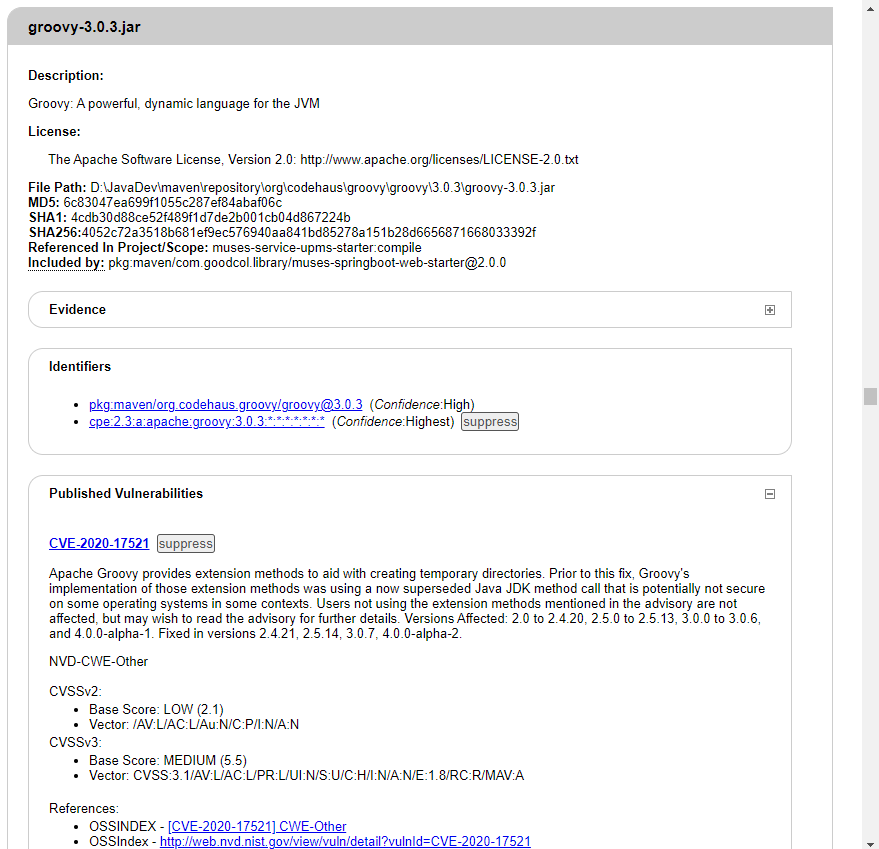
Maven 依赖漏洞扫描检查插件 dependency-check-maven 的使用
前言 在现代软件开发中,开源库的使用愈加普遍,然而这些开源库中的漏洞往往会成为潜在的安全风险。如何及时的发现依赖的第三方库是否存在漏洞,就变成很重要了。 本文向大家推荐一款可以进行依赖包漏洞检查的 maven 插件 dependency-check-m…...

2. 下载rknn-toolkit2项目
官网链接: https://github.com/airockchip/rknn-toolkit2 安装好git:[[1. Git的安装]] 下载项目: git clone https://github.com/airockchip/rknn-toolkit2.git或者直接去github下载压缩文件,解压即可。...

xhr、ajax、axois、fetch的区别
一、XMLHttpRequest (XHR)、AJAX、Axios 和 Fetch API 都是用于在不重新加载整个页面的情况下与服务器进行通信的技术和库。它们在处理超时、终止请求、进度反馈等机制上有一些显著的差异。以下是它们的详细比较: 1. XMLHttpRequest (XHR) XMLHttpRequest 是一种浏…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
