数学建模笔记——熵权法(客观赋权法)

熵权法(客观赋权法)

1. 基本概念

熵权法,物理学名词,按照信息论基本原理的解释,信息是系统有序程度的一个度量,熵是系统无序程度的一个度量;根据信息熵的定义,对于某项指标,可以用熵值来判断某个指标的离散程度,其信息熵值越小,指标的离散程度越大,该指标对综合评价的影响(即权重)就越大,如果某项指标的值全部相等,则该指标在综合评价中不起作用。因此,可利用信息熵这个工具,计算出各个指标的权重,为多指标综合评价提供依据。

• 熵权法是一种客观的赋权方法,它可以靠数据本身得出权重。
• 依据的原理:指标的变异程度越小,所反映的信息量也越少,其对应的权值也应该越低。

另一种表述：越有可能发生的事情，信息量越少。越不可能发生的事情，信息量就越多。其中我们认为 概率 就是衡量事情发生的可能性大小的指标。

那么把 信息量 用字母 $I$表示，概率用$P$表示，那么我们可以将它们建立一个函数关系：

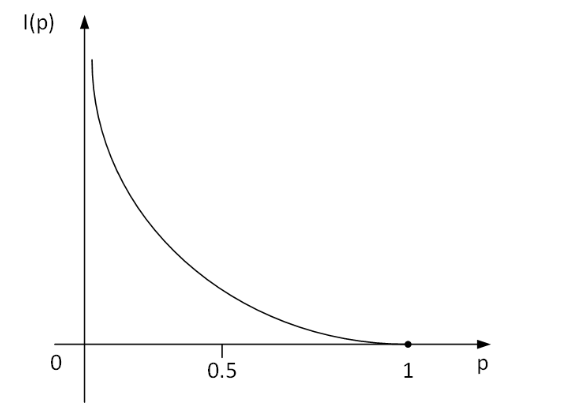
那么，假设 x 表示事件 X 可能发生的某种情况，p(x)表示这种情况发生的概率情况如上图所示，该图像可以用对数函数进行拟合，那
么最终我们可以定义：$I(x)=-\ln (p(x))$,因为$0\le p(x)\le 1$,所以$I(x)\ge 0$。

信息熵的定义

假设 x 表示事件 X 可能发生的某种情况，p(x) 表示这种情况发生的概率我们可以定义：$I(x)=-\ln (p(x))$ ,因为$0\le p(x)\le 1$ ,
所以$I(x)\ge 0$。如果事件 X 可能发生的情况分别为：$x_1,x_2,\cdots ,x_n$ ,那么我们可以定义事件 $X$ 的信息熵为：
$$H(X)=\sum _{i=1}^n\left[p(x_i)I(x_i)\right]=-\sum _{i=1}^n\left[p(x_i)\ln (p(x_i))\right]$$

那么从上面的公式可以看出，信息上的本质就是对信息量的期望值。

可以证明的是：$p(x_1)=p(x_1)=\cdots =p(x_n)=1/n$时，$H(x)$取最大值，此时$H(x)=\ln (n)$。(n表示事件发生情况的总数)

2. 基本步骤

熵权法的计算步骤大致分为以下三步：

1. 数据标准化

   假设有$n$个要评价的对象，$m$个评价指标(已经正向化了)构成的正向化矩阵如下：
   $$X=\left[\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1m}\\ x_{21}& x_{22}& \cdots & x_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ x_{n1}& x_{n2}& \cdots & x_{nm}\end{array}\right]$$
   设标准化矩阵为$Z$ ,$Z$中元素记为$z_{ij}:$
   $$z_{ij}=\frac{x_{ij}}{\sqrt{{\sum }_{i=1}^n{x}_{ij}^2}}$$
   判断$Z$矩阵中是否存在着负数，如果存在的话，需要对$X$使用另一种标准化方法对矩阵$X$进行一次标准化得到$Z$矩阵，其标准化的公式为：
   z i j = x i j − m i n { x 1 j , x 2 j , ⋯ , x n j } m a x { x 1 j , x 2 j , ⋯ , x n j } − m i n { x 1 j , x 2 j , ⋯ , x n j } z_{ij}=\frac{x_{ij}-min\{x_{1j},x_{2j},\cdots,x_{nj}\}}{max\{x_{1j},x_{2j},\cdots,x_{nj}\}-min\{x_{1j},x_{2j},\cdots,x_{nj}\}} zij​=max{x1j​,x2j​,⋯,xnj​}−min{x1j​,x2j​,⋯,xnj​}xij​−min{x1j​,x2j​,⋯,xnj​}​

   这样可以保证$z_{ij}$在 [0,1] 区间，没有负数。

2. 计算概率矩阵P

   假设有$n$个要评价的对象，$m$个评价指标，且经过了上一步处理得到的非负矩阵为：

   $$Z=\left[\begin{array}{cccc}{z}_{11}& z_{12}& \cdots & z_{1m}\\ z_{21}& z_{22}& \cdots & z_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ z_{n1}& z_{n2}& \cdots & z_{nm}\end{array}\right]$$
   计算概率矩阵$P$,其中$P$中每一个元素$p_{ij}$,的计算公式如下：
   $$p_{ij}=\frac{z_{ij}}{{\sum }_{i=1}^n{z}_{ij}}$$

   保证每一列的加和为1，即每个指标所对应的概率和为1。

3. 计算熵权

   信息熵的计算：

   对于第$j$个指标而言，其信息嫡的计算公式为：
   $$e_j=-\frac{1}{\ln n}\sum _{i=1}^n{p}_{ij}\ln (p_{ij}),(j=1,2,\cdots ,m)$$
   注意：这里如果说$p_{ij}$为0，那么就需要指定$ln(0)=0$ 。

   信息效用值的定义:
   $$d_j=1-e_j$$

   那么信息效用值越大，其对应的信息就越多。

   将信息效用值进行归一化，我们就能够得到每个指标的 熵权：
   $$\begin{array}{rl}{\omega }_j& =\frac{d_j}{{\sum }_{j=1}^m{d}_j},(j=1,2,3,\cdots ,m)\end{array}$$

3. 典型例题

明星Kun想找一个对象，但喜欢他的人太多，不知道怎么选，经过层层考察，留下三个候选人。他认为身高165是最好的，体重在90-100斤是最好的。

候选人	颜值	牌气(争吵次数)	身高	体重
A	9	10	165	120
B	8	7	166	80
C	6	3	164	90

• 观察候选人的数据我们可以发现，A，B，C三人的身高是极为接近的，那么对于找对象来说这个指标是不是就不重要了呢？

• 对于体重这个指标来说，三人相差较大，那么找对象是不是就多考虑这个指标？

3.1 正向化矩阵

候选人	颜值	脾气(争吵次数)	身高	体重
A	9	0	0	0
B	8	3	0.9	0.5
C	6	7	0.2	1

3.2 对正向化矩阵进行矩阵标准化

因为指标中没有负数，采用$z_{ij}=\frac{x_{ij}}{\sqrt{{\sum }_{i=1}^n{x}_{ij}^2}}$进行标准化

候选人	颜值	牌气(争吵次数)	身高	体重
A	0.669	0	0	0
B	0.595	0.394	0.976	0.447
C	0.446	0.919	0.217	0.894

3.3 计算概率矩阵P

计算标准化矩阵第$j$项指标下第$i$个样本所占的比重$p_{ij}=\frac{z_{ij}}{{\sum }_{i=1}^n{z}_{ij}}$

候选人	颜值	脾气(争吵次数)	身高	体重
A	0.391	0	0	0
B	0.348	0.300	0.818	0.333
C	0.261	0.700	0.182	0.667

3.4 计算熵权

颜值	脾气(争吵次数)	身高	体重
0.0085	0.3072	0.3931	0.2912

3.5 计算得分

候选人	得分
A	0.0044
B	0.5009
C	0.4946

4. python代码实现

import numpy as np
# 定义一个自定义的对数函数，用于处理输入数组中的零元素def mylog(p):n = len(p)lnp = np.zeros(n)for i in range(n):if p[i] == 0:lnp[i] = 0else:lnp[i] = np.log(p[i])return lnp# 定义一个指标矩阵
X = np.array([[9, 0, 0, 0], [8, 3, 0.9, 0.5], [6, 7, 0.2, 1]])# 对矩阵X的每一列进行标准化处理
Z = X/np.sqrt(np.sum(X**2, axis=0))
print("标准化后的矩阵为：\n{}".format(Z))# 计算熵权所需的变量和矩阵初始化
n, m = Z.shape
D = np.zeros(m)# 计算每个指标的信息效用值
for i in range(m):x = Z[:, i]p = x/np.sum(x)e = -np.sum(p*mylog(p))/np.log(n)D[i] = 1-e# 根据信息效用值计算各指标权重
W = D/np.sum(D)
print("各指标权重为：\n{}".format(W))

输出：

标准化后的矩阵为：
[[0.66896473 0.         0.         0.        ][0.59463532 0.3939193  0.97618706 0.4472136 ][0.44597649 0.91914503 0.21693046 0.89442719]]
各指标权重为：
[0.00856537 0.30716152 0.39326471 0.2910084 ]