一般位置下的3D齐次旋转矩阵
下面的矩阵虽然复杂,但它的逆矩阵求起来非常简单,只需要在 sin θ \sin\theta sinθ 前面加个负号就是原来矩阵的逆矩阵。
如果编程序是可以直接拿来用的,相比其它获取一般旋转轴不经过原点的三维旋转矩阵的途径或算法,应该能够一定程度降低计算或编程复杂度。如果是引用,这个叫 LC三维旋转矩阵公式(L和C是两作者的姓的首字母联合)。
得到这个结果没有什么取巧之处,纯粹就是堆计算量、靠眼力和数学公式化简的经验。本来以为只是再现了另一种罗德里格斯公式,但实际上并不是。
R ( x 0 , y 0 , z 0 , a , b , c , θ ) = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 2 − cos θ ] + ( sin θ [ 0 − c b 0 c 0 − a 0 − b a 0 0 0 0 0 0 ] a 2 + b 2 + c 2 \displaystyle R\left(x_0,y_0,z_0,a,b,c,\theta\right)=\left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 2-\cos \theta \\ \end{array} \right]+\left(\frac{\sin \theta \left[ \begin{array}{rrrr} 0 & -c & b & 0 \\ c & 0 & -a & 0 \\ -b & a & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} \right]}{\sqrt{a^2+b^2+c^2}} \right. R(x0,y0,z0,a,b,c,θ)= 1000010000100002−cosθ + a2+b2+c2sinθ 0c−b0−c0a0b−a000000
− ( 1 − cos θ ) ( [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ] − [ a b c 0 ] . [ a b c 0 ] a 2 + b 2 + c 2 ) ) . [ 1 0 0 − x 0 0 1 0 − y 0 0 0 1 − z 0 0 0 0 1 ] \displaystyle {\left.-(1-\cos \theta) \left(\left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right]-\frac{\left[ \begin{array}{c} a \\ b \\ c \\ 0 \\ \end{array} \right].\left[ \begin{array}{cccc} a & b & c & 0 \\ \end{array} \right]}{a^2+b^2+c^2}\right)\right).\left[ \begin{array}{rrrr} 1 & 0 & 0 & -{x_0} \\ 0 & 1 & 0 & -{y_0} \\ 0 & 0 & 1 & -{z_0} \\ 0 & 0 & 0 & 1 \\ \end{array} \right]} −(1−cosθ) 1000010000100001 −a2+b2+c2 abc0 .[abc0] . 100001000010−x0−y0−z01

相关文章:

一般位置下的3D齐次旋转矩阵
下面的矩阵虽然复杂,但它的逆矩阵求起来非常简单,只需要在 sin θ \sin\theta sinθ 前面加个负号就是原来矩阵的逆矩阵。 如果编程序是可以直接拿来用的,相比其它获取一般旋转轴不经过原点的三维旋转矩阵的途径或算法,应该能…...

每日一题——第八十六题
题目:写一个函数,输入一个十进制的数,将其转换为任意的r进制数 #include<stdio.h> void convertToBaseR(int num, int r); int main() {int num, r;printf("请输入十进制的整数:");scanf_s("%d", &…...

十、组合模式
组合模式(Composite Pattern)是一种结构型设计模式,它允许将对象组合成树形结构来表示“部分-整体”的层次关系。组合模式能够让客户端以统一的方式对待单个对象和对象集合,使得客户端在处理复杂树形结构的时候,可以以…...

一分钟了解网络安全风险评估!
网络安全风险评估是一种系统性的分析过程,旨在识别和评估网络系统中的潜在安全风险。这个过程包括识别网络资产、分析可能的威胁和脆弱性、评估风险的可能性和影响,以及提出缓解措施。网络安全风险评估有助于组织了解其网络安全状况,制定相应…...

【springsecurity】使用PasswordEncoder加密用户密码
目录 1. 导入依赖2. 配置 PasswordEncoder3. 使用 PasswordEncoder 加密用户密码4. 使用 PasswordEncoder 验证用户密码 1. 导入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-security</artifac…...

从0到1实现线程池(C语言版)
目录 🌤️1. 基础知识 ⛅1.1 线程概述 ⛅1.2 linux下线程相关函数 🌥️1.2.1 线程ID 🌥️1.2.2 线程创建 🌥️1.2.3 线程回收 🌥️1.2.4 线程分离 🌤️2. 线程池概述 ⛅2.1 线程池的定义 ⛅2.2 为…...

Visual studio自动添加头部注释
记事本打开VS版本安装目录下的Class.cs文件 增加如下内容:...

【C#生态园】提升性能效率:C#异步I/O库详尽比较和应用指南
优化异步任务处理:C#异步I/O库全面解析 前言 在C#开发中,异步I/O是一个重要的主题。为了提高性能和响应速度,开发人员需要深入了解各种异步I/O库的功能和用法。本文将介绍几个常用的C#异步I/O库,包括Task Parallel Library、Asy…...

管理医疗AI炒作的三种方法
一个人类医生和机器人医生互相伸手。 全美的医院、临床诊所和医疗系统正面临重重困难。他们的员工队伍紧张且人员短缺,运营成本不断上升,服务需求常常超过其承受能力,限制了医疗服务的可及性。 人工智能应运而生。在自ChatGPT推出将AI推向聚…...

VMware Workstation Pro Download 个人免费使用
参考 VMware Workstation Pro Download...
DevOps平台搭建过程详解--Gitlab+Jenkins+Docker+Harbor+K8s集群搭建CICD平台
一、环境说明 1.1CI/CD CI即为持续集成(Continue Integration,简称CI),用通俗的话讲,就是持续的整合版本库代码编译后制作应用镜像。建立有效的持续集成环境可以减少开发过程中一些不必要的问题、提高代码质量、快速迭代等;(Jenkins) CD即持续交付Con…...

Nginx之日志切割,正反代理,HTTPS配置
1 nginx日志切割 1.1 日志配置 在./configure --prefixpath指定的path中切换进去,找到log文件夹,进去后找到都是对应的日志文件 其中的nginx.pid是当前nginx的进程号,当使用ps -ef | grep nginx获得就是这个nginx.pid的值 在nginx.conf中…...
)
Mysql数据量大,如何拆分Mysql数据库(垂直拆分)
垂直拆分(Vertical Partitioning)是一种将数据库按照业务模块或功能进行拆分的方法,目的是将不同模块的数据放到不同的数据库中,从而减少单个数据库的压力,提高系统的性能和可扩展性。垂直拆分适用于数据量大且业务模块…...

机器人可能会在月球上提供帮助
登月是我们这个时代最具标志性的事件之一,这可能还算轻描淡写了:这是我们迄今为止在物理上探索得最远的一次。我听过一些当时的老广播,它们可以让你想象出这次航行的重要性。 现在,研究人员表示,我们可能很快就能重返…...
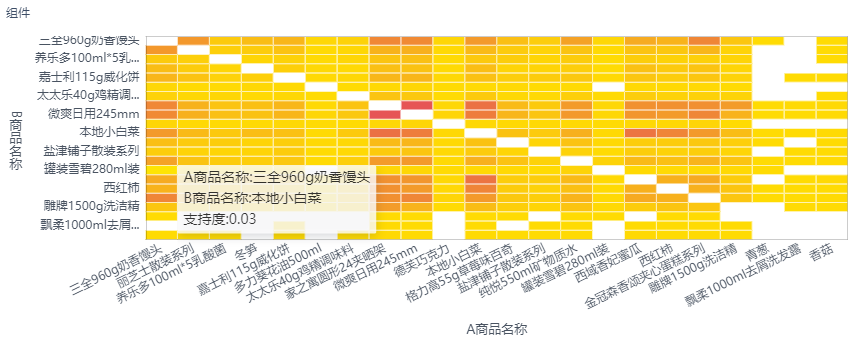
真实案例分享:零售企业如何避免销售数据的无效分析?
在零售业务的数据分析中,无效分析不仅浪费时间和资源,还可能导致错误的决策。为了避免这种情况,企业必须采取策略来确保他们的数据分析工作能够产生实际的商业价值。本文将通过行业内真实的案例,探讨零售企业如何通过精心设计的数…...

ctfshow-文件包含
web78 <?phpif(isset($_GET[file])){$file $_GET[file];include($file); }else{highlight_file(__FILE__); } 判断是否存在file参数 如果存在 将包含这个参数值 文件 php://filter可以获取指定文件源码。当它与包含函数结合时,php://filter流会被当作php文件执…...

Qt事件处理机制
用qt实现简单闹钟 widget.h #ifndef WIDGET_H #define WIDGET_H #include<QPushButton> #include<QTextEdit> #include<QLabel> #include <QWidget> #include<QMouseEvent> #include<QPoint> #include<QTime> #include<QTimer&…...

vue axios 如何读取项目下的json文件
在 Vue 项目中,使用 axios 读取本地的 JSON 文件可以通过将 JSON 文件放置在 public 目录中,然后通过 axios 发起请求读取。 步骤: 将 JSON 文件放置在 public 目录下: Vue 项目中的 public 目录是静态资源目录,项目编…...

燃气涡轮发动机性能仿真程序GSP12.0.4.2使用经验(二):使用GSP建立PG9351FA燃气轮机性能仿真模型
目录 一、PG9351FA燃气轮机简介及热力循环参数二、基于GSP的性能仿真模型设置环境参数设置进气道参数设置压气机参数设置燃烧室参数设置透平(涡轮)参数设置转子负载参数燃油流量外部控制 三、仿真结果四、其它 一、PG9351FA燃气轮机简介及热力循环参数 …...

迟滞比较器/施密特触发器
功能 从下面原理图像看来,只有在达到上下阈值才会出现输出电平的转换,这样防止信号的杂波跳变。而且每次的阈值是随着输出而变化的,当输出高时,阈值如下图中,V_PV_N V_R*( RF/(R1RF) )VH*( R1/(R1RF) );当输出低时&a…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
