位置编码Positional Encoding
位置编码Positional Encoding
- 1.Transformers中的PE
- 2.什么是Transformer位置编码
- 2.1.表格型
- 2.2.相对位置的关系-函数型
- 3.为什么可以表示相对距离?
- 4.其他参考
内容全来自于网络总结。
- 其他参考1
- 其他参考2
1.Transformers中的PE
- 摘抄自这里。

公式是初中生都看的懂,
- dmodeld_{model}dmodel表示输入的维度,
- pospospos表示单词的索引,
- iii表示向量中索引,
- 用sinsinsin,coscoscos计算出对应值,
但是为什么可以这样加到input上达到位置编码的效果呢?这时候看看bert就是非常直观的绝对位置动态编码,就直观很多,每个位置就是固定的embedding:

原文作者解释的:

对于任何偏移量k,对pos+k的编码都可以是pos编码线形变换.先来看看可视化结果:

值得注意的是,每个向量第0和第1的位置,第0的位置对应于PE公式的sin式,第1的位置对应于PE公式的cos式子,但是他们的2i都是0,所以会有下式:

所以每个输入向量的第0个和第1个位置的位置编码只和向量所处的pos有关.但是第3个位置后就受d_model影响了,一旦d_model变小,sin/cos函数就会有“拉伸”感,如下图所示:

对于长度为20的input,维度是50,可以画出一下PE值:

越小的pos受影响的i就越少,iii如果很大,PE值就会在0和1进行变换.从上图中,我们看到30~50列值基本没有变化.为啥上图这种编码就能学到位置信息?其实有种非常直观的解释方式,比如让你对数字进行编码,最直观的想法就是二进制编码,如下图所示:

PE方法就可以简单的理解为上述版本的float编码.
2.什么是Transformer位置编码
- 摘抄自这里。

在以前的模型中,NLP的每个Sequence都是一个token一个token的输入到模型当中。比如有一句话是“我喜欢吃洋葱”,那么输入模型的顺序就是“我”,“喜”,“欢“,”吃“,”洋“,”葱”,一个字一个字的。
上面的输入方式其实就引入了一个问题。一个模型每次只吃了一个字,那么模型只能学习到前后两个字的信息,无法知道整句话讲了什么。为了解决这个问题,Transformer模型引用了Self-attention来解决这个问题。Self-attention的输入方式如下:

可以看到,对于Self-attention结果而言,它可以一次性的将所有的字都当做输入。但是NLP的输入是有特点的,其特点是输入的文本要按照一定的顺序才可以。因为,文本的顺序是带有一部分语义关系的。比如下面两句话,不同的语序就有不同的语义。
- 句子1:我喜欢吃洋葱
- 句子2:洋葱喜欢吃我
所以,对于Transformer结构而言,为了更好的发挥并行输入的特点,首先要解决的问题就是要让输入的内容具有一定的位置信息。在原论文中,为了引入位置信息,加入了Position机制。
对于Transformer而言,Position机制看似简单,其实不容易理解。这篇文章通过梳理位置信息的引入方式,然后详细讲解在Transformer中是如何做的。最后将通过数学来证明为什么这种编码方式可以引入相对的位置信息。
位置编码分类:总的来说,位置编码分为两个类型:函数型和表格型
-
函数型:通过输入token位置信息,得到相应的位置编码
-
表格型:建立一个长度为L的词表,按词表的长度来分配位置id
2.1.表格型
- 方法一:使用[0,1]范围分配
这个方法的分配方式是,将0-1这个范围的,将第一个token分配0,最后一个token分配去1,其余的token按照文章的长度平均分配。具体形式如下:
- 我喜欢吃洋葱 【0 0.16 0.32.....1】
- 我真的不喜欢吃洋葱【0 0.125 0.25.....1】
问题:可以看到,如果句子长度不同,那么位置编码是不一样,所以无法表示句子之间有什么相似性。
- 方法二:1-n正整数范围分配
这个方法比较直观,就是按照输入的顺序,一次分配给token所在的索引位置。具体形式如下:
- 我喜欢吃洋葱 【1,2,3,4,5,6】
- 我真的不喜欢吃洋葱【1,2,3,4,5,6,7】
问题:往往句子越长,后面的值越大,数字越大说明这个位置占的权重也越大,这样的方式无法凸显每个位置的真实的权重。
总结:过去的方法总有这样或者那样的不好,所以Transformer对于位置信息的编码做了改进。
2.2.相对位置的关系-函数型
相对位置编码的特点,关注一个token与另一个token距离的相对位置(距离差几个token)。位置1和位置2的距离比位置3和位置10的距离更近,位置1和位置2与位置3和位置4都只相差1。
还是按照上面"我喜欢吃洋葱"中的“我”为例,看看相对位置关系是什么样子的:

可以看到,使用相对位置的方法,可以清晰的知道单词之间的距离远近的关系。
Transformer的Position
类型:首先给一个定义:Transformer的位置信息是函数型的。在GPT-3论文中给出的公式如下:

细节:首先需要注意的是,上个公式给出的每一个Token的位置信息编码不是一个数字,而是一个不同频率分割出来,和文本一样维度的向量。向量如下:

不同频率是通过 wnw_nwn 来表示的。得到位置向量P之后,将和模型的embedding向量相加,得到进入Transformer模型的最终表示。

① 关于 wiw_iwi : wiw_iwi 是频率

② 关于 $ t$:这里的 $ t$ 就是每个token的位置,比如说是位置1,位置2,以及位置 n
3.为什么可以表示相对距离?
上文说过,这样的位置信息表示方法可以表示不同距离token的相对关系。这里我们通过数学来证明。
回顾下中学的三角函数正余弦公式:

-
已知某一个token的位置是 $pos $ ,如果某一个token表示为 pos+kpos+kpos+k ,那就表明这个位置距上一个token为 kkk 。
-
如果这时需要看看一个位置 $ pos$ 和 $ pos+k$ 这两个字符的关系。按照位置编码的的公式,可以计算 pos+kpos+kpos+k
的位置编码,其结果如下:

可以看看上面公式中,有一部分是似曾相识的:

根据上面的公式可以看出,似曾相识的部分带入 PEpos+kPE_{pos+k}PEpos+k 的公式中,带入之后的结果如下:

可以知道,距离K是一个常数,所有上面公式中 sin() 和 cos() 的计算值也是常数,可以表示为:

这样,就可以将 PEpos+kPE_{pos+k}PEpos+k 写成一个矩阵的乘法。

可以从上面的矩阵乘法角度看到,位置 pos 的编码与位置 pos+k 的编码是线性关系。
那么问题来了,上面的操作也只可以看到线性关系,怎么可以更直白地知道每个token的距离关系?
为了解答上面的问题,将 PEposPE_{pos}PEpos 和 PEpos+kPE_{pos+k}PEpos+k 相乘 (两个向量相乘),可以得到如下结果:

发现相乘后的结果为一个余弦的加和。这里影响值的因素就是 k 。如果两个token的距离越大,也就是K越大,根据余弦函数的性质可以知道,两个位置的 PE 相乘结果越小。这样的关系可以得到,如果两个token距离越远则乘积的结果越小。
其他
这样的方式虽说可以表示出相对的距离关系,但是也是有局限的。其中一个比较大的问题是:只能的到相对关系,无法得到方向关系。所谓的方向关系就是,对于两个token谁在谁的前面,或者谁在谁的后面是无法判断的。数学表示如下:

4.其他参考

为什么这么做有用:
- pos+K=5,在计算第 5 个单词的位置编码的时候
- pos=1,k=4
- pos=2,k=3

相关文章:

位置编码Positional Encoding
位置编码Positional Encoding1.Transformers中的PE2.什么是Transformer位置编码2.1.表格型2.2.相对位置的关系-函数型3.为什么可以表示相对距离?4.其他参考内容全来自于网络总结。 其他参考1其他参考2 1.Transformers中的PE 摘抄自这里。 公式是初中生都看的懂, …...
Java异步注解@Async详解
一、Async注解 Async的作用就是异步处理任务。 在方法上添加Async,表示此方法是异步方法;在类上添加Async,表示类中的所有方法都是异步方法;使用此注解的类,必须是Spring管理的类;需要在启动类或配置类中…...
macOS Big Sur 11.7.5 (20G1225) 正式版 ISO、PKG、DMG、IPSW 下载
本站提供的 macOS Big Sur 软件包,既可以拖拽到 Applications(应用程序)下直接安装,也可以制作启动 U 盘安装,或者在虚拟机中启动安装。 2023 年 3 月 27 日 (北京时间 28 日凌晨),…...

硬件语言Verilog HDL牛客刷题day02 组合逻辑部分
1.VL11 4位数值比较器电路 1.题目: 某4位数值比较器的功能表如下。请用Verilog语言采用门级描述方式,实现此4位数值比较器。 2.解题代码: timescale 1ns/1nsmodule comparator_4(input [3:0] A ,input [3:0] B ,output …...

【LM401】ADC采集代码解读
本文主要实现基于LM401模组,,测试ADC低功耗采集,详细解析代码基于计算方式 对于小白理解ADC有更详细的理解 【LM401】ADC采集代码解读1. 单片机ADC与DAC简单理解2. 模组ADC通道介绍3. ADC初始化4. 采集值的计算5.测试结果硬件基于易智联的LM401的LoRa模组…...

CSDN 编程竞赛四十期题解
竞赛总览 CSDN 编程竞赛四十期:比赛详情 (csdn.net) 竞赛题解 题目1、小鱼的航程 有一只小鱼,它上午游泳150公里,下午游泳100公里,晚上和周末都休息(实行双休日)。假设从周x(1<x<7)开…...

【TypeScript学习之路】泛型
【TypeScript学习之路】泛型 文章目录【TypeScript学习之路】泛型写在前面前言一、认识泛型1.1 什么是泛型1.2 泛型函数的使用二、泛型接口与泛型类2.1 泛型接口2.2 泛型类三、泛型约束写在前面 🤗这里是前端程序员小张! 🌻人海茫茫ÿ…...

数据分析学习项目:东京奥运会跳水评论分析
“中国跳水梦之队” ————有关东京奥运会跳水评论分析 导语 第32届夏季奥林匹克运动会于2021年07月23日-2021年08月08日在日本东京举办。 四年一届的奥运会可以说是世界瞩目的盛会,奥运健儿们在赛场上的精神风貌不只是代表了他们自身的运动精神,更昭…...
、OrderBy(排序并自定义排序规则))
Winform/Csharp中使用Linq的Where条件筛选、Select字段映射(左外连接并设置无匹配时默认值)、OrderBy(排序并自定义排序规则)
场景 Java8新特性-Stream对集合进行操作的常用API: Java8新特性-Stream对集合进行操作的常用API_streamapi操作集合_霸道流氓气质的博客-CSDN博客 上面讲的是在Java中使用Stream中对集合的常用操作。 在C#中Linq是有对应的类似的api。 完整和详细的用法可自行查…...

Linux-常用的Shell命令
文章目录前言常用的Shell命令文件和目录管理查看文件、目录信息查看文件内容查看文件类型查找文件查找内容查看目录大小创建文件删除文件拷贝文件移动文件创建目录删除目录拷贝目录压缩文件解压文件路径相关操作目录切换显示当前路径用户、用户组管理创建用户删除用户创建用户组…...

Go语言基础:数组定义及循环遍历
前言 大家好,我是沐风晓月,本文go语言入门-掌握go语言函数收录于《go语言学习专栏》专栏,此专栏带你从零开始学习go语言,持续更新中,欢迎点赞收藏。 🏠个人主页:我是沐风晓月 🧑个人…...

【树与二叉树】二叉树顺序结构实现以及堆的概念及结构--详解介绍
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:数据结构 🎯长路漫漫浩浩,万事皆有期待 文章目录1. 二叉树顺序结构2.…...

天狗实战(二)SpringBoot API开发详解 --SpringMVC注解+封装结果+支持跨域+打包(下)
本文目录 前言专栏介绍一、创建SpringBoot项目1.1 添加springboot依赖1.2 创建启动类1.3 创建控制器类1.4 Run 或 Debug二、开发图书管理API2.1 web层BookAdminControllerBookVO2.2 service层BookServiceBookServiceImplBookBO2.3 dal层...
实验一 Windows系统安全实验【网络安全】
实验一 Windows系统安全实验【网络安全】前言推荐实验一 Windows系统安全实验3.1 帐户和口令的安全设置3.1.1 实验目的3.1.2 实验环境3.1.3 实验内容和步骤1. 删除不再使用的帐户并禁用guest帐户2.启用密码策略和帐户锁定策略3.查看“用户权限分配”4.查看“用户组权限分配”5.…...
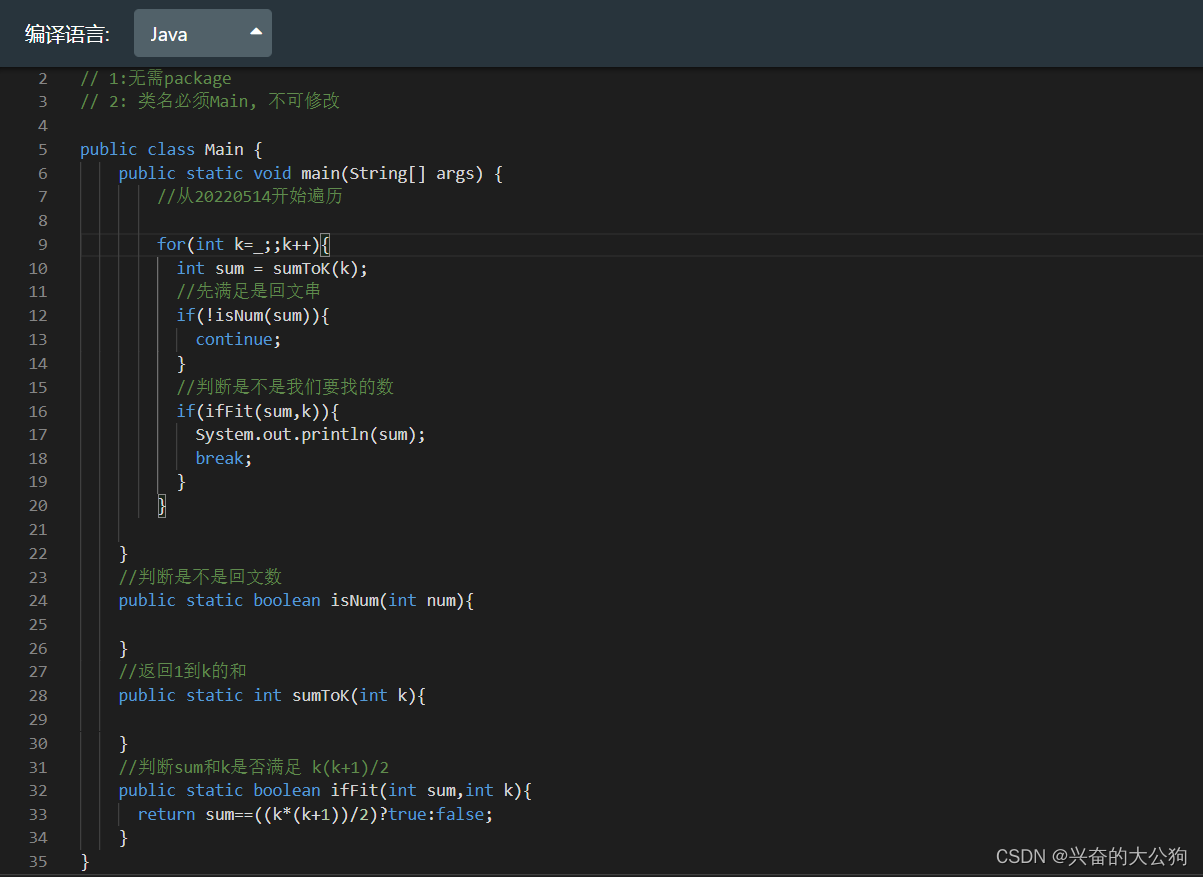
蓝桥杯正确的解题姿势
在做算法题的过程中最忌讳的就是上来就一顿乱敲,一开始我就是这样,但随着不断的刷题和老师的指导,总结了自己的刷题方法 示例题目 三角回文数 问题描述 对于正整数 n, 如果存在正整数 k使得 n123...kk(k1)/2 , 则 n 称为三角数。例如, 66066 …...

【mysql】性能优化
目录一、硬件与操作系统二、架构设计层面的优化三、mysql程序配置优化四、mysql执行优化一、硬件与操作系统 1.使用高性能cpu,提高计算能力 2.增大可用内存,提高读取能力 3.提高硬盘的读写速度,使用专用的固态硬盘 4.增大网络带宽,…...

Jupyter安装与远程使用过程记录
Jupyter安装与远程使用过程记录 文章目录Jupyter安装与远程使用过程记录Jupyter在线试用在服务器上安装Jupyter Notebook配置服务器远程连接首先保证ip地址连通性其次开启服务器访问端口然后在服务器启动服务最后测试连通性后续使用教程Jupyter在线试用 官网适用,感…...

Swift入门
基本数据类型 Int、UInt:整数型、非负整数Float、Double:单精度浮点数、双精度浮点数Bool:布偶值String、Character:字符串、字符 其他类型 Array, Dictionary:数组、字典StructClassvar:变量let&#x…...
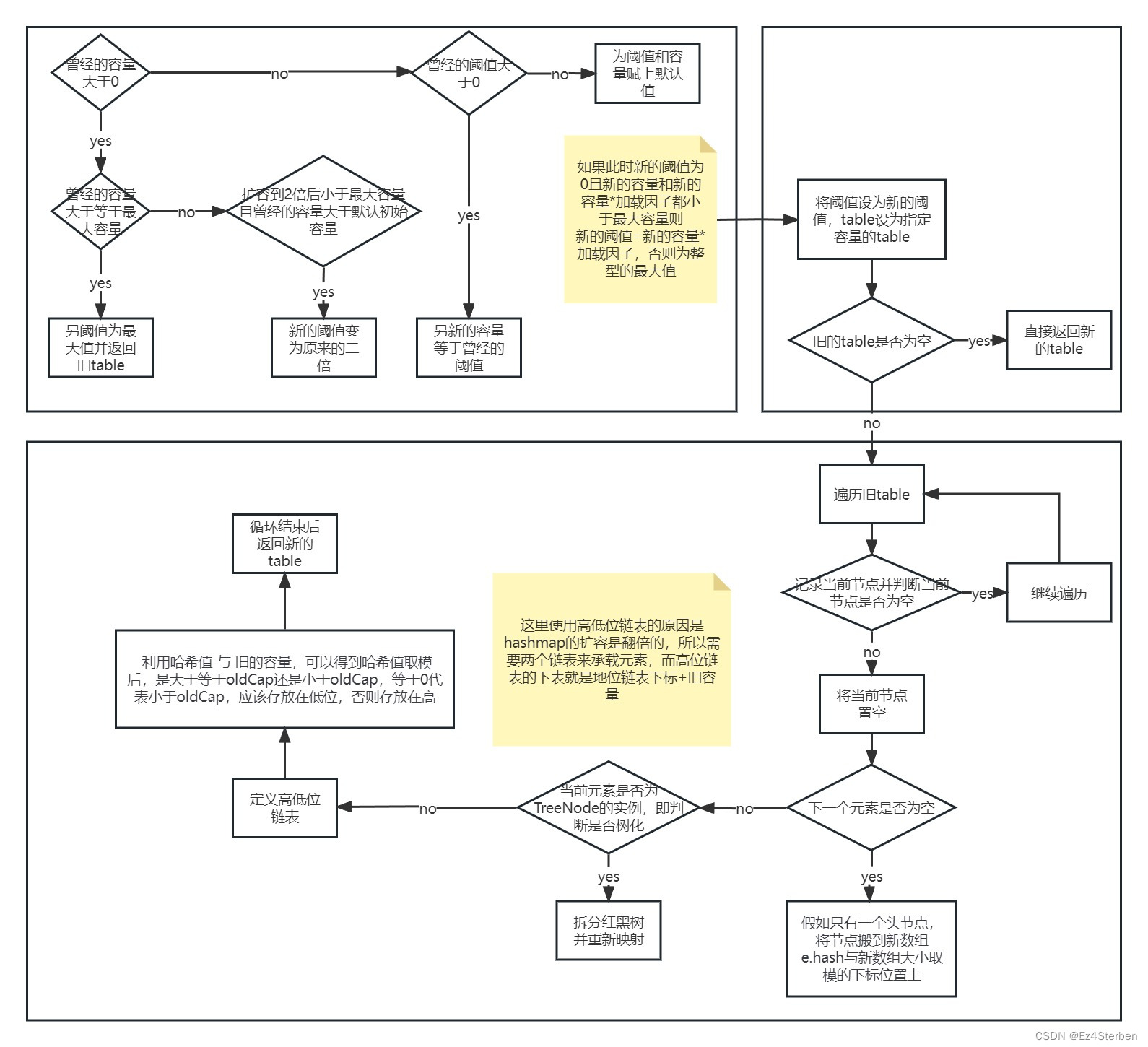
【HashMap】jdk1.8中HashMap的插入扩容源码学习分析
jdk1.8中HashMap的插入扩容源码学习分析 一、成员变量 首先介绍HashMap中各个成员变量的作用,在HashMap中有以下成员变量 size记录了HashMap中键值对的个数 loadFactor(加载因子)用来决定size达到容量的百分之多少时触发扩容机制 默认是0…...

Linux编译器-gcc/g++ 使用
在介绍gcc/g的使用前我们先了解一下两者的不同 gcc时主要编译c语言,而g主要编译c的,但是两者的选项是相同的,因此我们以gcc和c语言为例来讲解。背景知识 gcc和g都是编译器其核心作用将文本类文件翻译成二进制可执行 那么其过程是怎样的&…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...

Redis上篇--知识点总结
Redis上篇–解析 本文大部分知识整理自网上,在正文结束后都会附上参考地址。如果想要深入或者详细学习可以通过文末链接跳转学习。 1. 基本介绍 Redis 是一个开源的、高性能的 内存键值数据库,Redis 的键值对中的 key 就是字符串对象,而 val…...

智能体革命:企业如何构建自主决策的AI代理?
OpenAI智能代理构建实用指南详解 随着大型语言模型(LLM)在推理、多模态理解和工具调用能力上的进步,智能代理(Agents)成为自动化领域的新突破。与传统软件仅帮助用户自动化流程不同,智能代理能够自主执行工…...
