【树与二叉树】二叉树顺序结构实现以及堆的概念及结构--详解介绍

📝个人主页:@Sherry的成长之路
🏠学习社区:Sherry的成长之路(个人社区)
📖专栏链接:数据结构
🎯长路漫漫浩浩,万事皆有期待
文章目录
- 1. 二叉树顺序结构
- 2.堆
- 2.1 堆的概念及结构
- 2.1.1 概念
- 2.1.2 堆的性质
- 2.2 堆的概念选择题
- 2.3 堆的实现
- ①.堆的初始化:
- ②.堆的插入(向上调整算法):
- ③.堆的删除(向下调整算法):
- ④.取堆顶数据:
- ⑤.堆中数据个数:
- ⑥.堆的判空:
- ⑦.堆的销毁:
- ⑦.堆的打印:
- 2.4 堆的代码实现
- Heap.h 用于函数的声明
- Heap.c 用于函数的定义
- Test.c 用于测试函数
- 3.总结:
1. 二叉树顺序结构
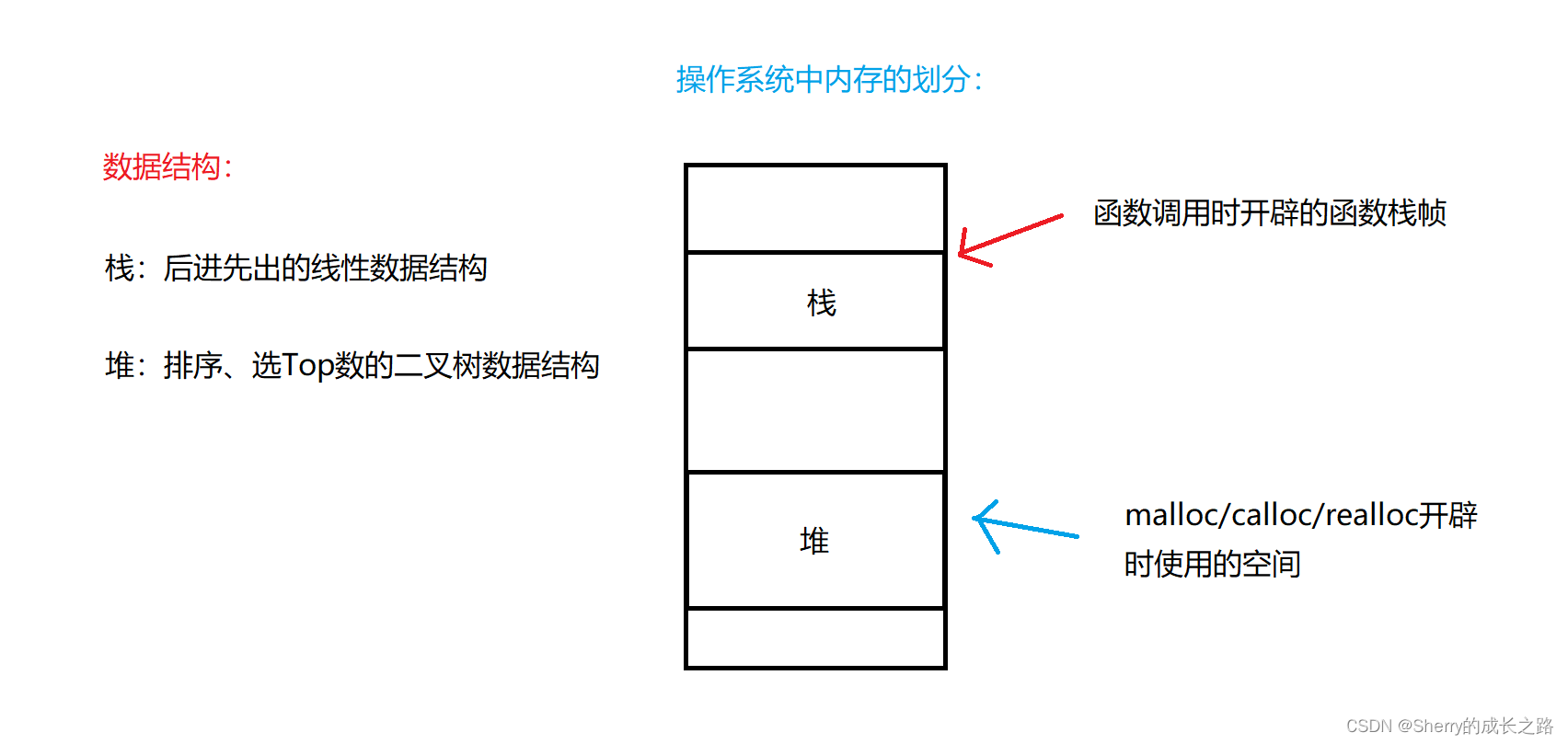
普通二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储。
注意 操作系统和数据结构中都有栈和堆的概念,这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
2.堆
2.1 堆的概念及结构
2.1.1 概念
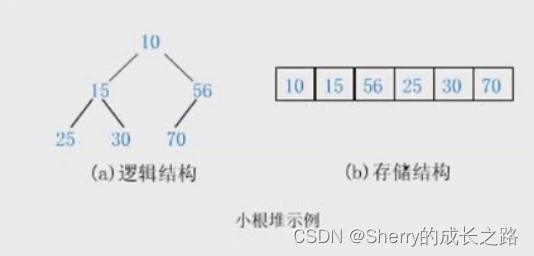
堆分为小根堆和大根堆,根节点始终小于子节点称为小根堆,相反根节点始终大于子节点则称为大根堆。换句话说,将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
▶ 大(根)堆,树中所有父亲都大于或者等于孩子,且大堆的根是最大值;

▶ 小(根)堆,树中所有父亲都小于或者等于孩子,且小堆的根是最小值;
2.1.2 堆的性质
▶ 堆中某个节点的值总是不大于或不小于其父节点的值;
▶ 堆总是一棵完全二叉树;
2.2 堆的概念选择题
1、下列关键字序列为堆的是( )
A. 100, 60, 70, 50, 32, 65
B. 60, 70, 65, 50, 32, 100
C. 65, 100, 70, 32, 50, 60
D. 70, 65, 100, 32, 50, 60
E. 32, 50, 100, 70, 65, 60
F. 50, 100, 70, 65, 60, 32
- 分析:根据堆的概念分析,A 选项为大根堆;

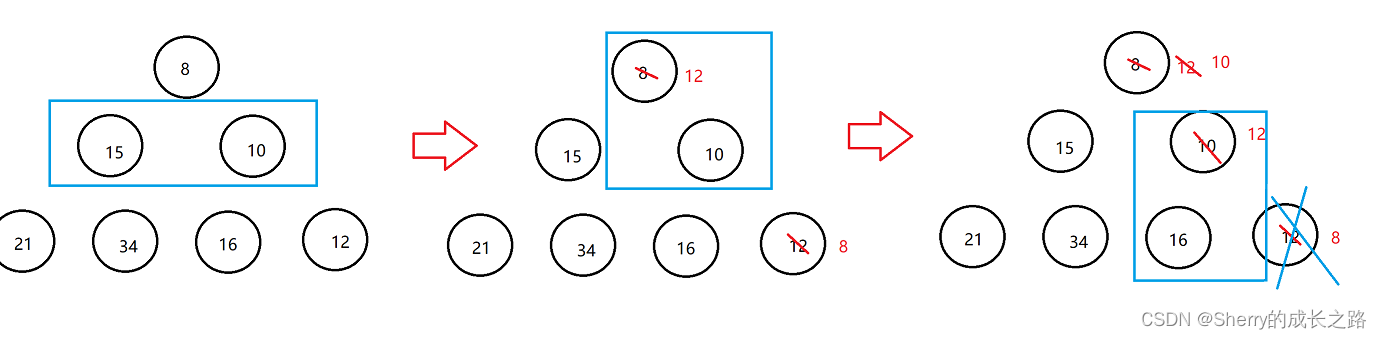
2、已知小根堆为 8, 15, 10, 21, 34, 16, 12,删除关键字 8 之后需重建堆,在此过程中,关键字之间的比较次数是( )
A. 1
B. 2
C. 3
D. 4
- 分析:此题考查的是建堆的过程,所以选择 C 选项
3、一组记录排序码为 (5 11 7 2 3 17),则利用堆排序方法建立的初始堆为( )
A. (11 5 7 2 3 17)
B. (11 5 7 2 17 3)
C. (17 11 7 2 3 5)
D. (17 11 7 5 3 2)
E. (17 7 11 3 5 2)
F. (17 7 11 3 2 5)
- 分析:此题考查的是堆排序建堆的过程,根据下面堆排序的过程分析,选择 C 选项

4、、注,请理解下面堆应用的知识再做。最小堆 [0, 3, 2, 5, 7, 4, 6, 8],在删除堆顶元素0之后,其结果是( )
A. [3,2,5,7,4,6,8]
B. [2,3,5,7,4,6,8]
C. [2,3,4,5,7,8,6]
D. [2,3,4,5,6,7,8]
- 分析:此题考查的是 Pop 堆顶后,重新建堆的变化,所以选择 C 选项

2.3 堆的实现
1、堆向下调整算法
向下调整算法有一个前提:左右子树必须是一个堆 (包括大堆和小堆),才能调整。
现在我们给出一个数组,逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。
1.1 建堆
有一个随机值的数组,把它理解成完全二叉树,并模拟成堆 (大堆/小堆)
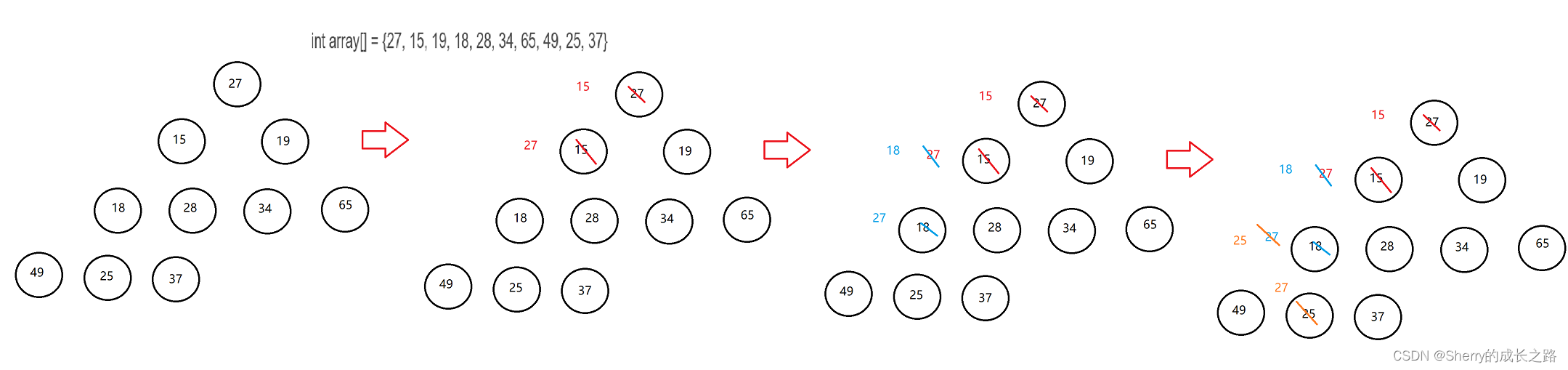
int array[] = {27, 15, 19, 18, 28, 34, 65, 49, 25, 37}
观察这组数据
根下面的左右子树都是小根堆,其实堆向下调整算法就是针对这种特殊数据结构
1.1.1针对于这种类型的数据应该怎么调堆
思路:从根开始与左右孩子比较,如果孩子比父亲小,则两两交换位置,再继续往下调,直到左右孩子都比父亲大或者调到叶子
1.1.2 如果不满足左右子树是堆,怎么调整?
int array[] = {27, 37, 28, 18, 19, 34, 65, 25, 49, 15}
根的左右子树 37、28 都不满足:这里的想法就是先让左右子树先满足;而对于左右子树 37、28 来说又需要让 37 先满足;这样依此类推直至满足堆的条件。那干脆就从倒数的第一棵树,也就是倒数的第一个非叶子节点开始调整
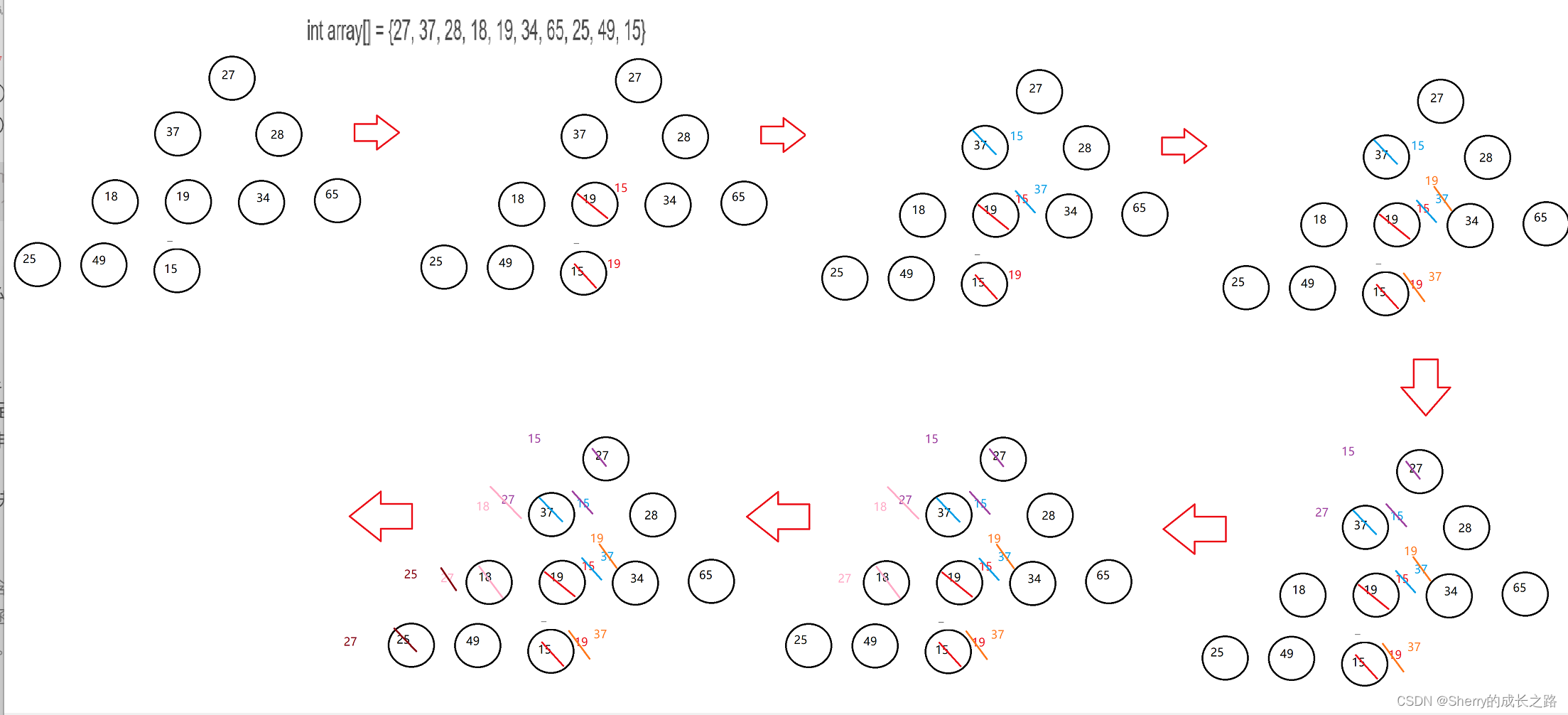
关于堆的实现我们使用标准模块化开发格式进行研究:
Heap.h:存放函数声明、包含其他头文件、定义宏。
Heap.c:书写函数定义,书写函数实现。
test.c:书写程序整体执行逻辑。
①.堆的初始化:
堆的初始化与队列相同,首先判断传入指针非空后,将其置空,并将数据置零即可。
//1、对于HeapCreate函数,结构体不是外面传进来的,而是在函数内部自己malloc空间,再创建的
/*
HP* HeapCreate(HPDataType* a, int n)
{}
*/
//2、对于HeapInit函数,在外面定义一个结构体,把结构体的地址传进来
void HeapInit(HP* php, HPDataType* a, int n)
{assert(php); //malloc空间(当前数组大小一样的空间)php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (php->a == NULL){printf("malloc fail\n");exit(-1);}//使用数组初始化memcpy(php->a, a, sizeof(HPDataType) * n);php->size = n;php->capacity = n;//建堆 int i = 0;for (i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(php->a, n, i);}
}
②.堆的插入(向上调整算法):
因为堆的存储在物理层面上数组,但是在逻辑层面上二叉树。并且由于只有小根堆和大根堆,所以在插入数据之后要想保证其仍然是堆,就需要进行适当的调整。
插入时从尾部插入,而是否为堆取决于子节点和父节点的关系,若为小根堆则子节点要比父节点要大,否则就需要交换子节点和父节点,大根堆则相反。而这种调整方式就叫做向上调整算法。
执行操作前需进行非空判断,防止堆空指针进行操作。
插入前判断空间是否足以用于此次扩容,若不足则进行扩容,直至满足插入条件后堪称插入操作,这个接口的功能实现也与队列的处理方式基本相同。
与队列的不同点在于,为了保证插入后仍然是堆,需要在插入后使用向上调整算法进行适当的调整。
//向上调整算法:
//除了child的数据,前面的数构成堆
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0)//parent>=0 感觉有问题 但可以使用{if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}//堆插入:
void HeapPush(HP* php, HPDataType x)
{assert(php);//空间不够,增容if (php->size == php->capacity){HPDataType* temp = (HPDataType*)realloc(php->a, php->capacity * 2 * sizeof(HPDataType));if (temp == NULL){printf("realloc fail\n");exit(-1);}else{php->a = temp; }php->capacity *= 2;}//将x放在最后php->a[php->size] = x;php->size++;//向上调整AdjustUp(php->a, php->size - 1);
}③.堆的删除(向下调整算法):
堆删除的实质是删除堆顶元素,如果我们直接删除堆顶的元素,再将数据挪动,就会破坏堆的结构,所以这种方法并不可取;于是我们这里采用将堆顶的数据与最后一个数据交换,再删除最后一个数据的方法,这样就实现了堆顶数据的删除。接着我们再调整一下堆顶数据的位置即可。
在这里选择的调整方法是:将根节点与它的孩子中的较小值交换,然后再将交换后的节点作为父节点继续与它的子节点交换,直到该节点小于它的子节点,或者成为叶节点。
注意 使用这个方法有一个前提:根节点的两个子树也得是堆才行。而这种方法就叫做向下调整算法。
执行操作前需进行非空判断,防止对空指针进行操作。
删除过程同样与队列近乎一致,不同点是在删除过后为了保证删除堆顶数据后仍为堆,于是需要使用向下调整算法对删除后的结果进行适当的处理。
//向下调整算法:
//左右子树都是大堆或小堆
void AdjustDown(HPDataType* arr, int n, int parent)
{int child = parent * 2 + 1;while (child < n){//选出左右孩子中大的那一个if (child + 1 < n && arr[child] < arr[child + 1])//防止越界 右孩子存在//child + 1 < n 放左边 先检查{child++;//右孩子>左孩子 ++}if (arr[child] > arr[parent]){Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else//父亲大于孩子 不用交换了{break;}}
}//堆顶数据删除:
void HeapPop(HP* php)
{assert(php);//没有数据删除就报错assert(!HeapEmpty(php));//交换首尾Swap(&php->a[0], &php->a[php->size-1]);php->size--;//向下调整AdjustDown(php->a, php->size, 0);
}
HPDataType HeapTop(HP* php)
{assert(php);//没有数据获取就报错assert(!HeapEmpty(php));return php->a[0];
}
int HeapSize(HP* php)
{assert(php);return php->size;
}
测试删除接口功能实现:
④.取堆顶数据:
取堆顶数据操作与队列完全相同
HPDataType HeapTop(HP* php)
{assert(php);//没有数据获取就报错assert(!HeapEmpty(php));return php->a[0];
}⑤.堆中数据个数:
查看堆中的数据个数操作很简单,在判断传入指针非空后,直接返回 p->size 的值,即堆中保存的数据数量即可。
int HeapSize(HP* php)
{assert(php);return php->size;
}
⑥.堆的判空:
堆的判空操作与队列完全相同
//堆数据判空:
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}
⑦.堆的销毁:
堆的销毁与队列相同
void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}
⑦.堆的打印:
void HeapPrint(HP* php)
{assert(php);int i = 0;for (i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");
}
2.4 堆的代码实现
注意
▶ 堆的初始化一般是使用数组进行初始化的
▶ 堆的插入数据不分头插、尾插,将数据插入后,原来堆的属性不变
先放在数组的最后一个位置,再向上调整
▶ 堆的删除数据删除的是堆顶的数据,将数据删除后,原来堆的属性不变
为了效率,将第一个和最后一个元素交换,再减容,然后再调整
Heap.h 用于函数的声明
#pragma once//头
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<string.h>
#include<stdbool.h>typedef int HPDataType;//C++ -> priority_queue 在C++里用的是优先级队列,其底层就是一个堆
//大堆
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;
//函数的声明
//交换
void Swap(HPDataType* px, HPDataType* py);
//向下调整
void AdjustDown(HPDataType* arr, int n, int parent);
//向上调整
void AdjustUp(HPDataType* a, int child);
//使用数组进行初始化
void HeapInit(HP* php, HPDataType* a, int n);
//回收空间
void HeapDestroy(HP* php);
//插入x,保持它继续是堆
void HeapPush(HP* php, HPDataType x);
//删除堆顶的数据,保持它继续是堆
void HeapPop(HP* php);
//获取堆顶的数据,也就是最值
HPDataType HeapTop(HP* php);
//判空
bool HeapEmpty(HP* php);
//堆的数据个数
int HeapSize(HP* php);
//输出
void HeapPrint(HP* php);
Heap.c 用于函数的定义
#include"Heap.h"void Swap(HPDataType* px, HPDataType* py)
{HPDataType temp = *px;*px = *py;*py = temp;
}
//左右子树都是大堆或小堆
void AdjustDown(HPDataType* arr, int n, int parent)
{int child = parent * 2 + 1;while (child < n){//选出左右孩子中大的那一个if (child + 1 < n && arr[child] < arr[child + 1])//防止越界 右孩子存在//child + 1 < n 放左边 先检查{child++;//右孩子>左孩子 ++}if (arr[child] > arr[parent]){Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else//父亲大于孩子 不用交换了{break;}}
}
//除了child的数据,前面的数构成堆
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0)//parent>=0 感觉有问题 但可以使用{if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
void HeapPrint(HP* php)
{assert(php);int i = 0;for (i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");
}
//1、对于HeapCreate函数,结构体不是外面传进来的,而是在函数内部自己malloc空间,再创建的
/*
HP* HeapCreate(HPDataType* a, int n)
{}
*/
//2、对于HeapInit函数,在外面定义一个结构体,把结构体的地址传进来
void HeapInit(HP* php, HPDataType* a, int n)
{assert(php); //malloc空间(当前数组大小一样的空间)php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (php->a == NULL){printf("malloc fail\n");exit(-1);}//使用数组初始化memcpy(php->a, a, sizeof(HPDataType) * n);php->size = n;php->capacity = n;//建堆 int i = 0;for (i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(php->a, n, i);}
}
void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}
void HeapPush(HP* php, HPDataType x)
{assert(php);//空间不够,增容if (php->size == php->capacity){HPDataType* temp = (HPDataType*)realloc(php->a, php->capacity * 2 * sizeof(HPDataType));if (temp == NULL){printf("realloc fail\n");exit(-1);}else{php->a = temp; }php->capacity *= 2;}//将x放在最后php->a[php->size] = x;php->size++;//向上调整AdjustUp(php->a, php->size - 1);
}
void HeapPop(HP* php)
{assert(php);//没有数据删除就报错assert(!HeapEmpty(php));//交换首尾Swap(&php->a[0], &php->a[php->size-1]);php->size--;//向下调整AdjustDown(php->a, php->size, 0);
}
HPDataType HeapTop(HP* php)
{assert(php);//没有数据获取就报错assert(!HeapEmpty(php));return php->a[0];
}
int HeapSize(HP* php)
{assert(php);return php->size;
}
Test.c 用于测试函数
#include"Heap.h"void TestHeap()
{int arr[] = { 27, 37, 28, 18, 19, 34, 65, 25, 49, 15 };HP hp;HeapInit(&hp, arr, sizeof(arr)/sizeof(arr[0]));HeapPrint(&hp);HeapPush(&hp, 18);HeapPrint(&hp);HeapPush(&hp, 98);HeapPrint(&hp);printf("\n\n");//将堆这数据结构实现好后,我们就可以利用这些接口实现排序while(!HeapEmpty(&hp)){printf("%d ", HeapTop(&hp)); HeapPop(&hp);}printf("\n");}
int main()
{TestHeap();return 0;
}
3.总结:
今天我们认识并学习了二叉树顺序结构的相关概念,并且对堆的概念及结构也有了一定的了解。还对二叉树顺序存储的实例——堆的各接口功能进行了实现。下一篇博客我们将从堆的时间复杂度详解以及堆的应用—堆排序、TOP - K问题进一步介绍堆。希望我的文章和讲解能对大家的学习提供一些帮助。
当然,本文仍有许多不足之处,欢迎各位小伙伴们随时私信交流、批评指正!我们下期见~

相关文章:

【树与二叉树】二叉树顺序结构实现以及堆的概念及结构--详解介绍
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:数据结构 🎯长路漫漫浩浩,万事皆有期待 文章目录1. 二叉树顺序结构2.…...

天狗实战(二)SpringBoot API开发详解 --SpringMVC注解+封装结果+支持跨域+打包(下)
本文目录 前言专栏介绍一、创建SpringBoot项目1.1 添加springboot依赖1.2 创建启动类1.3 创建控制器类1.4 Run 或 Debug二、开发图书管理API2.1 web层BookAdminControllerBookVO2.2 service层BookServiceBookServiceImplBookBO2.3 dal层...
实验一 Windows系统安全实验【网络安全】
实验一 Windows系统安全实验【网络安全】前言推荐实验一 Windows系统安全实验3.1 帐户和口令的安全设置3.1.1 实验目的3.1.2 实验环境3.1.3 实验内容和步骤1. 删除不再使用的帐户并禁用guest帐户2.启用密码策略和帐户锁定策略3.查看“用户权限分配”4.查看“用户组权限分配”5.…...
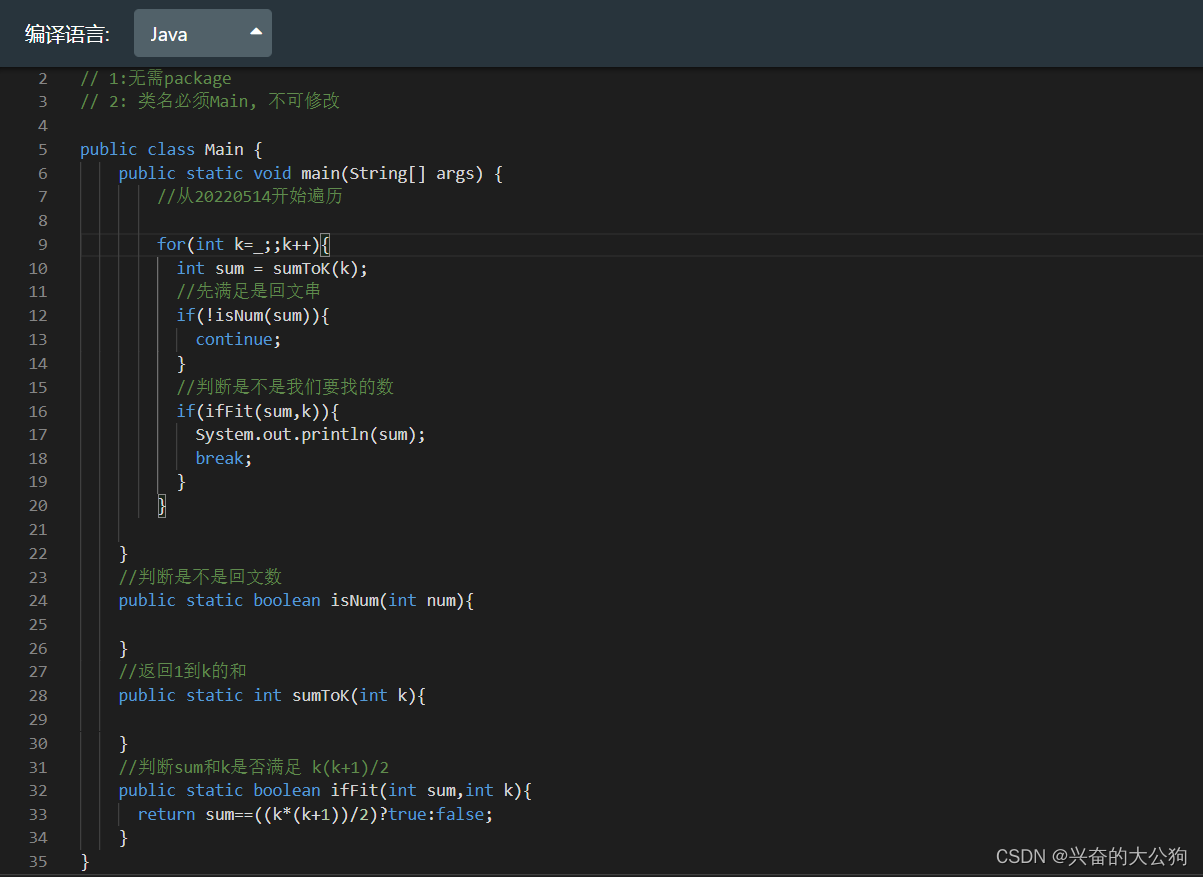
蓝桥杯正确的解题姿势
在做算法题的过程中最忌讳的就是上来就一顿乱敲,一开始我就是这样,但随着不断的刷题和老师的指导,总结了自己的刷题方法 示例题目 三角回文数 问题描述 对于正整数 n, 如果存在正整数 k使得 n123...kk(k1)/2 , 则 n 称为三角数。例如, 66066 …...

【mysql】性能优化
目录一、硬件与操作系统二、架构设计层面的优化三、mysql程序配置优化四、mysql执行优化一、硬件与操作系统 1.使用高性能cpu,提高计算能力 2.增大可用内存,提高读取能力 3.提高硬盘的读写速度,使用专用的固态硬盘 4.增大网络带宽,…...

Jupyter安装与远程使用过程记录
Jupyter安装与远程使用过程记录 文章目录Jupyter安装与远程使用过程记录Jupyter在线试用在服务器上安装Jupyter Notebook配置服务器远程连接首先保证ip地址连通性其次开启服务器访问端口然后在服务器启动服务最后测试连通性后续使用教程Jupyter在线试用 官网适用,感…...

Swift入门
基本数据类型 Int、UInt:整数型、非负整数Float、Double:单精度浮点数、双精度浮点数Bool:布偶值String、Character:字符串、字符 其他类型 Array, Dictionary:数组、字典StructClassvar:变量let&#x…...
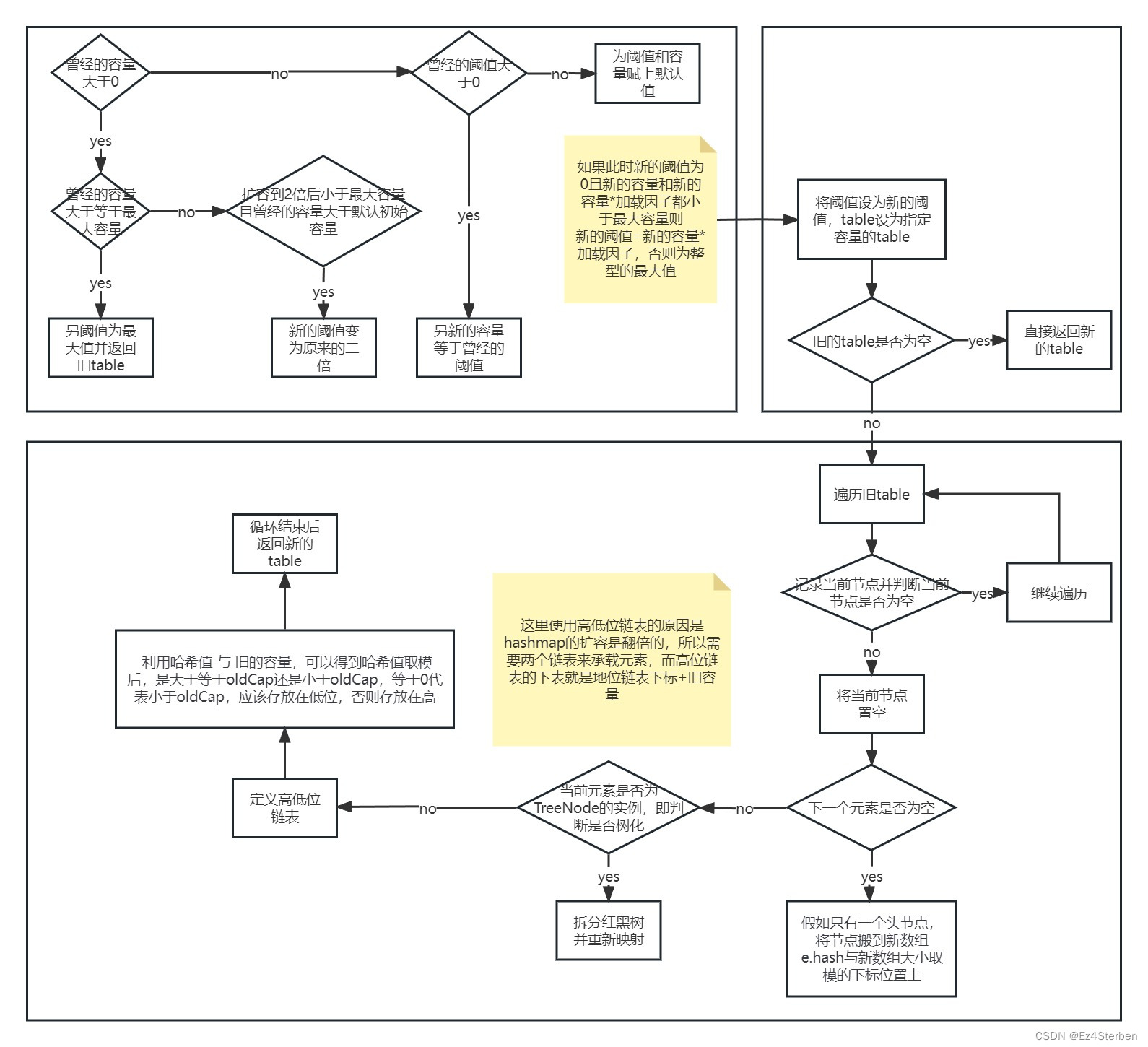
【HashMap】jdk1.8中HashMap的插入扩容源码学习分析
jdk1.8中HashMap的插入扩容源码学习分析 一、成员变量 首先介绍HashMap中各个成员变量的作用,在HashMap中有以下成员变量 size记录了HashMap中键值对的个数 loadFactor(加载因子)用来决定size达到容量的百分之多少时触发扩容机制 默认是0…...

Linux编译器-gcc/g++ 使用
在介绍gcc/g的使用前我们先了解一下两者的不同 gcc时主要编译c语言,而g主要编译c的,但是两者的选项是相同的,因此我们以gcc和c语言为例来讲解。背景知识 gcc和g都是编译器其核心作用将文本类文件翻译成二进制可执行 那么其过程是怎样的&…...

网络安全专家最爱用的9大工具
网络安全专家,不是你认为的那种搞破坏的 “黑客”。网络安全专家,即 “ethical hackers”,是一群专门模拟网络安全专家攻击,帮助客户了解自己网络的弱点,并为客户提出改进建议的网络安全专家。 网络安全专家在工作中&a…...

Linux内核设计与实现第四章学习笔记
文章目录Linux内核设计与实现第四章学习笔记具体场景Linux调度算法传统的调度公平调度调度的实现时间记账调度器实体虚拟实时进程选择调度器入口睡眠和唤醒抢占和上下文切换用户抢占内核抢占实时调度策略Linux内核设计与实现第四章学习笔记 进程优先级:Linux中采用…...
i.MX9352——介绍一款多核异构开发板
本篇来介绍一款多核异构的Linux开发板——OK-MX9352-C开发板。 1 开发板硬件介绍 OK-MX9352-C开发板由核心板和底板组成,核心板采用处理器芯片为NXP的i.MX9352,这是一款多核异构的芯片,核心板基础配置如下 CPU:2Cortex-A551.5G…...
【Python】一文学会面向对象?当然可以的
文章目录前言一、万物皆对象二、类也是对象三,元类总结前言 在大家学习python的时候,一定听说过一句话: 在我们python中万物皆对象,不管是整数、字符串、列表、字典这些基本数据类型,还是函数、以及自定义类创建出来…...

ElasticSearch - SpringBoot整合ES:精确值查询 term
文章目录00. 数据准备01. ElasticSearch 结构化搜索是什么?02. ElasticSearch 结构化搜索方式有哪些?03. ElasticSearch 全文搜索方式有哪些?04. ElasticSearch term 查询数字?05. ElasticSearch term 查询会不会计算评分…...

【GPT4】微软对 GPT-4 的全面测试报告(2)
欢迎关注【youcans的GPT学习笔记】原创作品,火热更新中 微软对 GPT-4 的全面测试报告(1) 微软对 GPT-4 的全面测试报告(2) 【GPT4】微软对 GPT-4 的全面测试报告(2)2. 多模态与跨学科的组合&…...
Docker打包exe运行环境
Docker打包exe运行环境 本文运行环境 Window安装Docker环境 修改配置 点击Switch to Window containers OS/Arch 变为 windows/amd64 拉取window镜像 访问Nano Server找到需要的Window版本拉取镜像 运行镜像测试 进入到容器内部 其他内容就自由发挥啦~~ 参考内容…...
springboot+vue田径运动会成绩管理系统java
springboot是基于spring的快速开发框架, 相比于原生的spring而言, 它通过大量的java config来避免了大量的xml文件, 只需要简单的生成器便能生成一个可以运行的javaweb项目, 是目前最火热的java开发框架 田径运动会成绩管理系统,主要的模块包括首页、个人中心、赛…...

我能“C”——详解操作符(上)
目录 1.操作符的分类: 2. 算数操作符 3.移位操作符 4.位操作符 5.赋值操作符 6.单目操作符 7.关系操作符 8.逻辑操作符 THE END 1.操作符的分类: 操作符也叫运算符 算术操作符 移位操作符 位操作符 赋值操作符 单目操作符 关系操作符 逻辑…...

第一章Vue基础
文章目录前端发展史前端三要素JavaScript框架UI框架JavaScript构建工具三端合一什么是VueVue的好处什么是MVVM为什么要使用MVVM环境配置第一个Vue程序声明式渲染模板语法绑定样式数据绑定为什么要实现数据的双向绑定el与data的两种写法条件渲染事件驱动事件的基本用法事件修饰符…...

【虚幻引擎UE】UE5核心效率插件推荐
一、UnrealEditorPythonScripts (基于UE5 的Python支持插件) 支持Python语言基于UE5进行开发 GIT地址:https://github.com/mamoniem/UnrealEditorPythonScripts 二、Haxe-UnrealEngine5 (基于UE5 的Haxe支持插件) Haxe是一门新兴的开源编程语言,是一种开源的编程语言。…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
