动态规划-分割回文串ⅡⅣ
在本篇博客中将介绍分割回文串Ⅱ以及分割回文串Ⅳ这两个题目。
分割回文串Ⅱ
题目描述
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文串。 返回符合要求的 最少分割次数 。
示例:
输入:s = "aabac"
输出:2
解释:只需2次分割就可将 s 分割成 ["a","aba","c"] 这样3个回文子串。
解题思路
为了解决这个问题,我们可以使用动态规划(Dynamic Programming, DP)的方法。具体来说,我们可以先计算出字符串 s 中所有子串是否是回文串,并存储这个结果,以便后续使用。然后,我们再次使用动态规划来找出将字符串 s 分割成回文子串所需的最少分割次数。
第一步:判断子串是否为回文
我们定义一个二维数组 dp1[i][j],其中 dp1[i][j] 表示从索引 i 到索引 j 的子串 s[i...j] 是否是回文串。我们可以从字符串的两端向中间遍历,并更新这个数组(这部分与此前回文子串一题中相同 动态规划-回文子串-CSDN博客)。
第二步:动态规划求解最少分割次数
这一步的动态规划思路主要是基于已经判断好的回文子串信息,来求解将整个字符串 s 分割成多个回文子串所需的最少分割次数。这里的关键在于利用动态规划来避免重复计算,并逐步构建出整个问题的解。
- 定义状态:
- 定义
dp2[i]表示将字符串s的前i+1个字符(即s[0...i])分割成多个回文子串所需的最少分割次数。
- 定义
- 初始化:
dp2[0]初始化为 0,因为空字符串不需要分割。
- 状态转移:
- 对于每个位置
i(从 1 到n-1,其中n是字符串s的长度),我们需要找到所有可能的分割点j(从 0 到i-1),使得s[j+1...i]是一个回文串。这可以通过查询之前计算好的dp1数组来实现,其中dp1[j+1][i]表示s[j+1...i]是否为回文串。 - 如果找到了这样的
j,那么我们可以将s[0...i]分割为s[0...j]和s[j+1...i]两部分,其中s[j+1...i]已经是一个回文串,不需要进一步分割。因此,s[0...i]的最少分割次数就是s[0...j]的最少分割次数(即dp2[j])加上 1(因为我们在j和i之间进行了一次分割)。 - 我们需要遍历所有可能的
j,并更新dp2[i]为这些分割方案中的最小值。
- 对于每个位置
- 结果:
- 最终,
dp2[n-1]就是整个字符串s的最少分割次数。
- 最终,
代码示例
class Solution {
public:int minCut(string s) {int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n, false));for (int i = 0; i < n; i++) {dp[i][i] = true; // 单个都是回文子串if (i + 1 < n && s[i] == s[i + 1]) { // 两个相同的字符构成回文子串dp[i][i + 1] = true;}}for (int len = 3; len <= n; len++) { // 从字串长度为3开始遍历for (int i = 0; i < 1 + n - len; i++) { // i+len-1<nint j = i + len - 1;if (s[i] == s[j] && dp[i + 1][j - 1] == true) {dp[i][j] = true;}}}vector<int> f(n,INT_MAX); // f[i]: 从0到i 的子串 所符合要求的 最少分割次数f[0] = 0;for (int i = 1; i < n; i++) {if (dp[0][i] == true) { // 从0到i 的子串是回文串f[i] = 0;} else {for (int j = 0; j <= i; j++) {if (dp[j][i]) {f[i] = min(f[j - 1] + 1, f[i]);}}}}return f[n - 1];}
};分割回文串Ⅳ
题目描述
给你一个字符串 s ,如果可以将它分割成三个 非空 回文子字符串,那么返回 true ,否则返回 false 。
当一个字符串正着读和反着读是一模一样的,就称其为 回文字符串 。
示例 1:
输入:s = "abcbdad"
输出:true
解释:"abcbdd" = "a" + "bcb" + "dad",三个子字符串都是回文的。
示例 2:
输入:s = "abaccdef"
输出:false
解释:s 没办法被分割成 3 个回文子字符串。
解题思路
这一题与上题相似,要解决这个问题,我们可以采用一种比较直观的方法,即遍历所有可能的分割点,然后检查每个分割点形成的三个子字符串是否都是回文串。为了高效地检查一个子字符串是否是回文串,我们可以先预处理一个二维数组(或者使用一个函数),用于快速判断任意子字符串是否为回文。
第一步:初始化动态规划数组
- 定义一个二维布尔数组
dp,其中dp[i][j]表示字符串s从索引i到索引j(包含两端)的子串是否是回文子串。 - 初始化对角线元素
dp[i][i]为true,因为单个字符自然是回文子串。 - 初始化相邻元素
dp[i][i+1]为true,如果s[i]和s[i+1]相等,因为两个相同的字符也构成回文子串。
第二步:填充动态规划数组
- 使用两层循环遍历所有可能的子串长度(从3开始,因为长度为1和2的情况已经在第一步中处理过了)和起始位置。
- 对于每个子串,检查其首尾字符是否相等,并且去掉首尾字符后的子串(即
dp[i+1][j-1])是否是回文子串。如果这两个条件都满足,则当前子串是回文子串,将dp[i][j]设置为true。
第三步:检查是否存在有效的分割
- 使用两层循环遍历所有可能的分割点(第一个和第二个分割点),以检查是否存在一种分割方式,使得字符串
s被分为三个非空回文子串。 - 对于每个分割点组合
(i, j),其中i是第一个分割点的位置(不包括),j是第二个分割点的位置(不包括),检查dp[0][i-1]、dp[i][j-1]和dp[j][n-1]是否都为true。如果是,则表示找到了一个有效的分割方式,返回true。 - 如果遍历完所有可能的分割点组合后都没有找到有效的分割方式,则返回
false。
代码示例
class Solution {
public:bool checkPartitioning(string s) {int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n, false));for (int i = 0; i < n; i++) {dp[i][i] = true; // 单个都是回文子串if (i + 1 < n && s[i] == s[i + 1]) { // 两个相同的字符构成回文子串dp[i][i + 1] = true;}}for (int len = 3; len <= n; len++) { // 从字串长度为3开始遍历for (int i = 0; i < 1 + n - len; i++) { // i+len-1<nint j = i + len - 1;if (s[i] == s[j] && dp[i + 1][j - 1] == true) {dp[i][j] = true;}}}for (int i = 0; i < n - 1; i++) {for (int j = i + 1; j < n - 1; j++) {if (dp[0][i] && dp[i + 1][j] && dp[j + 1][n - 1]) {return true;}}}return false;}
};相关文章:

动态规划-分割回文串ⅡⅣ
在本篇博客中将介绍分割回文串Ⅱ以及分割回文串Ⅳ这两个题目。 分割回文串Ⅱ 题目描述 给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文串。 返回符合要求的 最少分割次数 。 示例: 输入:s "aabac" 输…...

Python编码系列—Python项目维护与迭代:持续进化的艺术
🌟🌟 欢迎来到我的技术小筑,一个专为技术探索者打造的交流空间。在这里,我们不仅分享代码的智慧,还探讨技术的深度与广度。无论您是资深开发者还是技术新手,这里都有一片属于您的天空。让我们在知识的海洋中…...
【鸿蒙开发工具报错】Build task failed. Open the Run window to view details.
Build task failed. Open the Run window to view details. 问题描述 在使用deveco-studio 开发工具进行HarmonyOS第一个应用构建开发时,通过Previewer预览页面时报错,报错信息为:Build task failed. Open the Run window to view details.…...

k8s集群部署:容器运行时
1. 卸载旧版本 Docker # 卸载旧版本的 Docker 组件 sudo yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotate \docker-engine注释: 该命令会移除系统中现有的 Docker 及其相关组件࿰…...

PHP7 的内核结构
PHP7 是 PHP 语言的一个重要版本,带来了许多性能提升和语言特性改进。要深入了解 PHP7 的内核,我们需要探讨其设计和实现的关键方面,包括 PHP 的执行模型、内存管理、编译和优化过程等。 1. PHP7 的内核结构 1.1 执行模型 PHP 是一种解释型…...
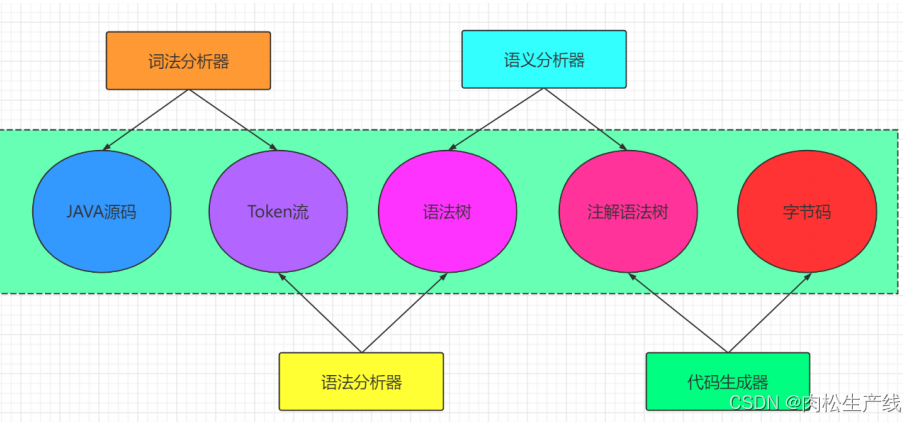
JVM合集
序言: 1.什么是JVM? JVM就是将javac编译后的.class字节码文件翻译为操作系统能执行的机器指令翻译过程: 前端编译:生成.class文件就是前端编译后端编译:通过jvm解释(或即时编译或AOT)执行.class文件时跨平台的,jvm并不是跨平台的通过javap进行反编译2.java文件是怎么变…...
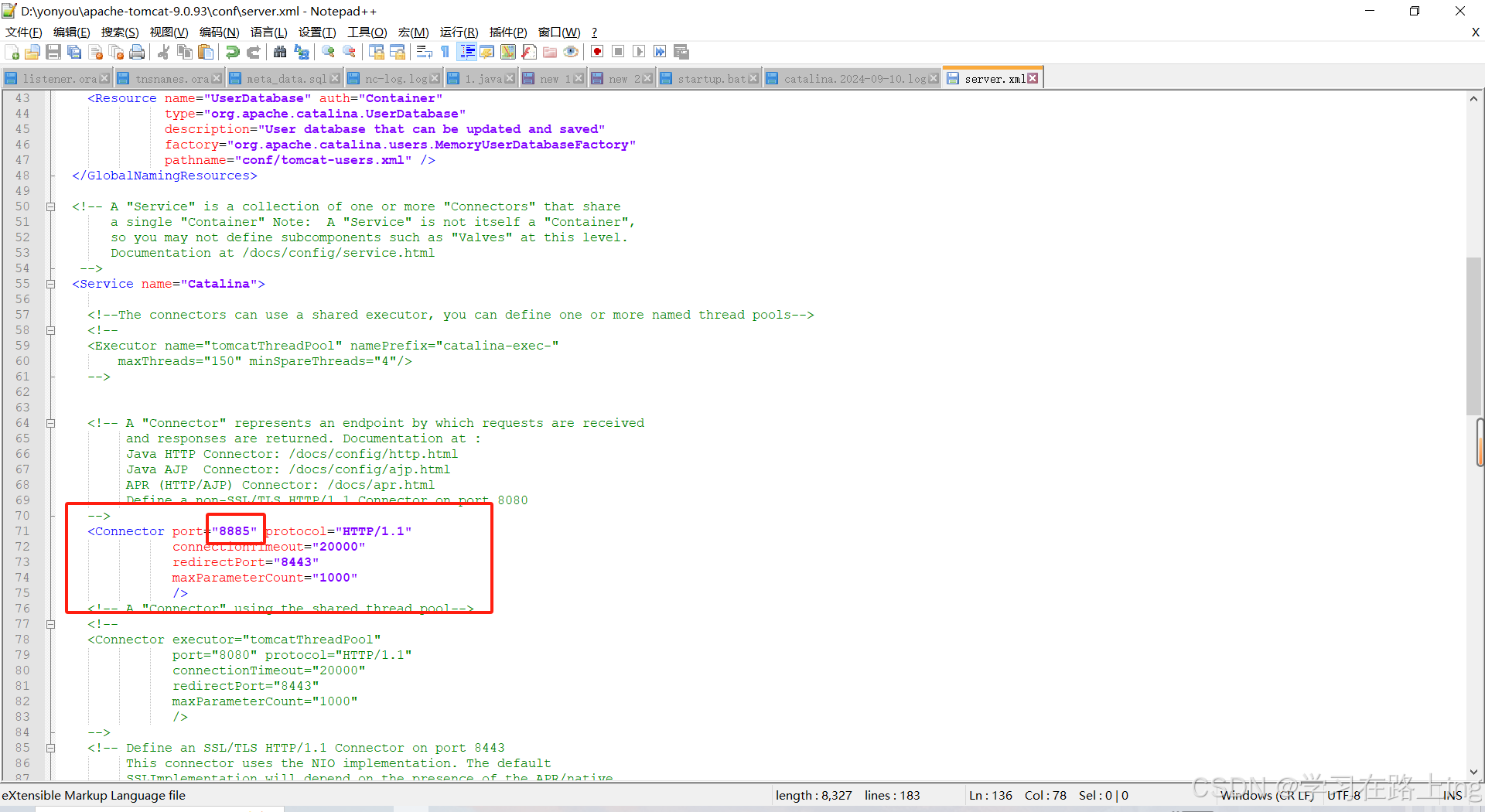
tomcat端口被占用解决方法
在安装目录的conf下修改server.xml文件,修改后保存重启即可...
全新的训练算法:Reflection 70B进入大众的视野
在2024年9月6日,大模型的圈子迎来了一位新成员——Reflection 70B,它横扫了MMLU、MATH、IFEval、GSM8K等知名的模型基准测试,完美超越了GPT-4o,同时也超越了Claude3.5 Sonnet成为了新的大模型之王,Reflection 70B到底是…...

静态标注rtk文件参数解析
目录 在静态标注中,rtk(Real-Time Kinematic)文件的主要作用 rtk文件包含几种类型数据 具体作用 具体示例 %RAWIMUSA #INSPVAXA $GPRMC 背景: 最近工作中涉及到静态标注 slam相关,因为初入门,对于rtk文件中有很多参数&…...

TensorFlow和PyTorch小知识
TensorFlow和PyTorch是当前最流行的两个开源机器学习库,它们都广泛用于研究和工业界的深度学习项目。下面是对它们的介绍: 1,TensorFlow - **开发背景:** TensorFlow最初由Google Brain Team开发,并于2015年11月开源…...

Java证书信息收集
1.Java二级 【NCRE 二级Java语言程序设计02】考试流程及二级Java大纲_java语言程序设计计算机二级-CSDN博客...

flink写入hudi MOR表
第一步:创建flink内存表从kafka读取数据: DROP TABLE IF EXISTS HUDI_KAFKA_DEBEZIUM_ZHANG; CREATE TABLE IF NOT EXISTS HUDI_KAFKA_DEBEZIUM_ZHANG( ID STRING comment 编码 ,NAME STRING comment 名称 ,PRIMARY KEY(RCLNT,RLDNR,RRCTY,RVERS,RYEAR,…...
 :三个世界--“存在的意义”-“‘我’的价值的实现” 之2)
智能工厂程序设计 之-2 (Substrate) :三个世界--“存在的意义”-“‘我’的价值的实现” 之2
Q13、我刚看了一下前门前面的讨论。有一段文字您的重新 理解一下。那就是: 对题目 的另一角度( “智能工厂的程序设计”的三个层次词 分别关注的问题 及其 解决 思路的描述)的解释: 三个不同层次(深度)&…...

概要设计例题
答案:A 知识点: 概要设计 设计软件系统的总体结构:采用某种方法,将一个复杂的系统按照功能划分成模块;确定每个模块的功能;确定模块之间的调用关系;确定模块之间的接口,即模块之间…...

注册表模式:使用注册表和装饰器函数的模块化设计
在现代软件开发中,模块化设计是提高代码可维护性和可扩展性的关键技术之一。本文将探讨如何使用注册表(Registry)和装饰器函数(Decorator Function)来实现模块化设计,提升代码的灵活性和可扩展性。 什么是…...
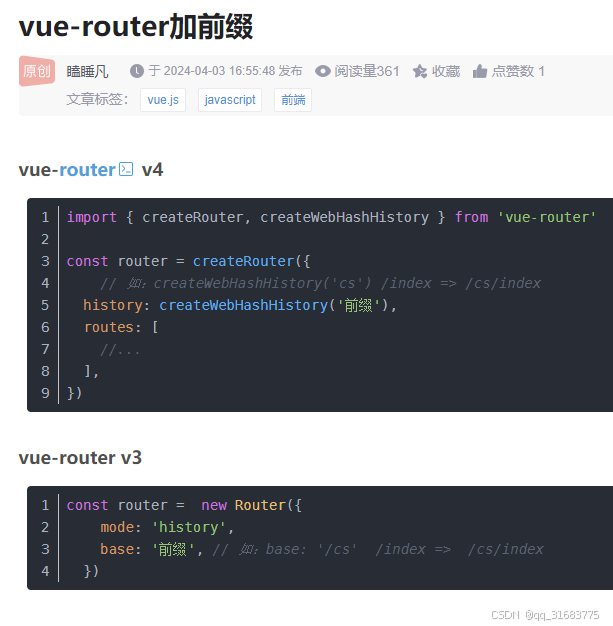
怎样将vue项目 部署在ngixn的子目录下
如果同一服务器的80端口下,需要部署两个或以上数量的vue项目,那么就需要将其中一个vue项目部署在根目录下,其他的项目部署在子目录下. 像这样的配置 访问根目录 / 访问灭火器后台管理,访问 /mall/ 访问商城的后台管理 那么商场的vue项目,这样配置,才能在/mall/下正常访问? 1…...
FPGA开发:Verilog数字设计基础
EDA技术 EDA指Electronic Design Automation,翻译为:电子设计自动化,最早发源于美国的影像技术,主要应用于集成电路设计、FPGA应用、IC设计制造、PCB设计上面。 而EDA技术就是指以计算机为工具,设计者在EDA软件平台上…...

哈希表,算法
一.什么是哈希表 哈希表是一种用于快速数据存取的数据结构。它通过哈希函数将键(key)映射到表中的一个位置,从而实现高效的插入、删除和查找操作。 二.哈希冲突 哈希冲突发生在多个键通过哈希函数映射到哈希表的同一位置时。由于哈希表的大…...

Java数组的定义及遍历
数组的声明 长度不能超过定义的长度。超过则会报错通过下标来访问 数组的遍历 最常用最简单的方法是增强for循环。...

【电路笔记】-反相运算放大器
反相运算放大器 文章目录 反相运算放大器1、概述2、理想反相运算放大器3、实际反相运算放大器3.1 闭环增益3.2 输入阻抗3.3 输出阻抗4、反相运算放大器示例5、总结1、概述 上一篇关于同相运算放大器的文章中已介绍了该运算放大器配置的所有细节,该配置在同相引脚 (+) 上获取输…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...
