代码随想录训练营 Day56打卡 图论part06 108. 冗余连接 109. 冗余连接II

代码随想录训练营 Day56打卡 图论part06

一、卡码108. 冗余连接

题目描述
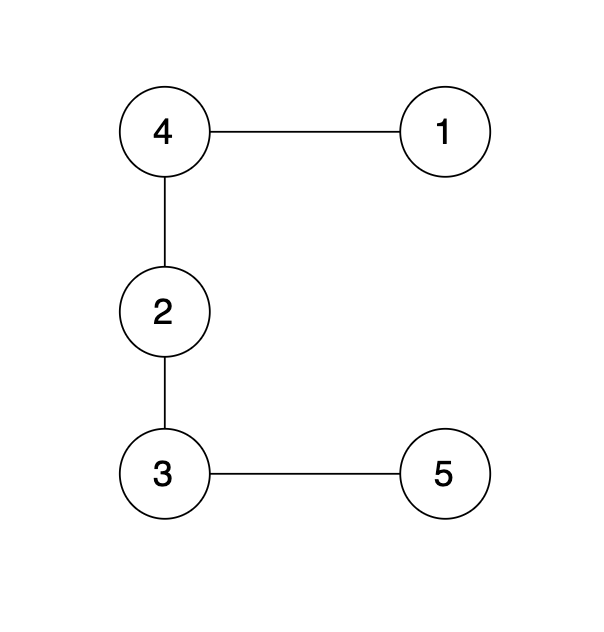
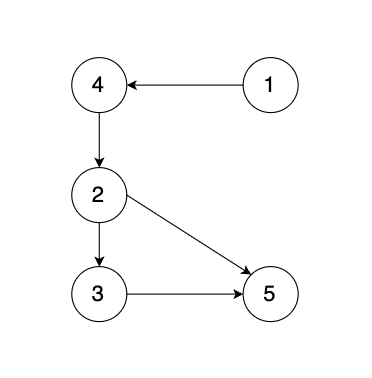
有一个图，它是一棵树，他是拥有 n 个节点（节点编号1到n）和 n - 1 条边的连通无环无向图（其实就是一个线形图），如图：

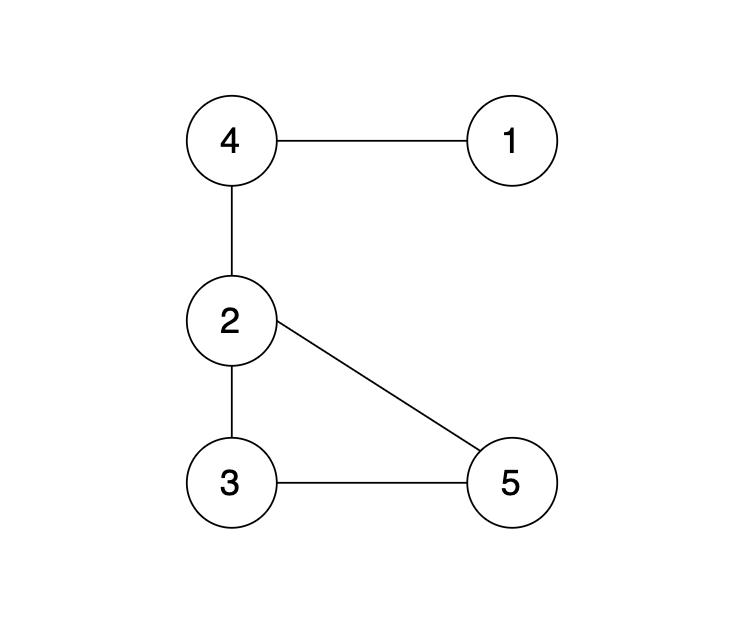
现在在这棵树上的基础上，添加一条边（依然是n个节点，但有n条边），使这个图变成了有环图，如图：

先请你找出冗余边，删除后，使该图可以重新变成一棵树。
输入描述
第一行包含一个整数 N，表示图的节点个数和边的个数。
后续 N 行，每行包含两个整数 s 和 t，表示图中 s 和 t 之间有一条边。
输出描述
输出一条可以删除的边。如果有多个答案，请删除标准输入中最后出现的那条边。
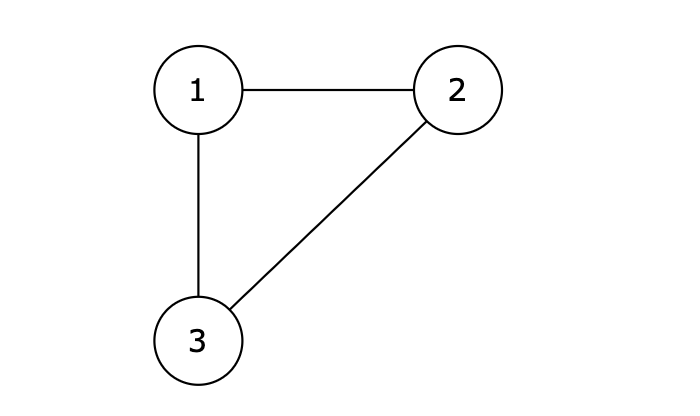
输入示例
3
1 2
2 3
1 3
输出示例
1 3
提示信息

图中的 1 2，2 3，1 3 等三条边在删除后都能使原图变为一棵合法的树。但是 1 3 由于是标准输出里最后出现的那条边，所以输出结果为 1 3

1. 树的性质：一棵树有 n 个节点和 n-1 条边，是一个连通且无环的图。如果给一棵树多加一条边，那么它就会形成一个环。
2. 寻找冗余边：使用并查集来判断每次加边时，是否会形成环。如果发现某一条边连接的两个节点已经属于同一个连通分量（即它们已经连通），说明这条边是冗余的，即它会导致环的出现。
3. 返回结果：根据题目要求，返回输入中最后出现的那条冗余边。

代码实现

class Solution:def findRedundantConnection(self, edges: list[list[int]]) -> list[int]:n = len(edges)  # 由于题目给定 n 条边，所以有 n 个节点parent = list(range(n + 1))  # 初始化并查集，每个节点的父节点初始化为它自己# 并查集的 find 函数，使用路径压缩优化def find(index: int) -> int:if parent[index] != index:  # 如果当前节点的父节点不是自己parent[index] = find(parent[index])  # 递归找到根节点，并将路径上的所有节点直接指向根节点return parent[index]  # 返回根节点# 并查集的 union 函数，合并两个节点所在的集合def union(index1: int, index2: int):parent[find(index1)] = find(index2)  # 将 index1 的根节点连接到 index2 的根节点# 遍历所有边，执行并查集的合并操作for node1, node2 in edges:if find(node1) != find(node2):  # 如果 node1 和 node2 不在同一个集合中union(node1, node2)  # 合并它们的集合else:return [node1, node2]  # 如果 node1 和 node2 已经在同一个集合中，说明这条边是冗余边return []  # 题目保证输入合法，所以不会执行到这里

卡码题目链接
题目文章讲解

二、卡码109. 冗余连接II

题目描述
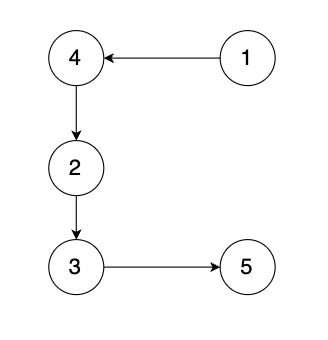
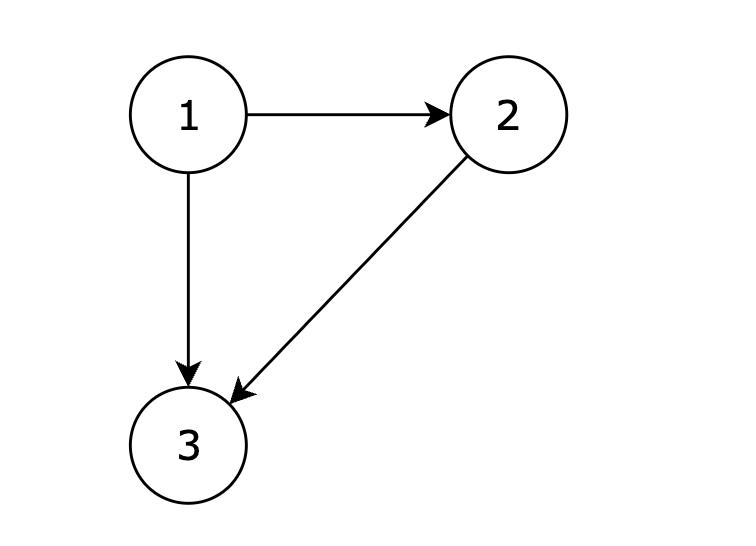
有一种有向树,该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。有向树拥有 n 个节点和 n - 1 条边。如图：

现在有一个有向图，有向图是在有向树中的两个没有直接链接的节点中间添加一条有向边。如图：

输入一个有向图，该图由一个有着 n 个节点(节点编号 从 1 到 n)，n 条边，请返回一条可以删除的边，使得删除该条边之后该有向图可以被当作一颗有向树。
输入描述
第一行输入一个整数 N，表示有向图中节点和边的个数。
后续 N 行，每行输入两个整数 s 和 t，代表这是 s 节点连接并指向 t 节点的单向边
输出描述
输出一条可以删除的边，若有多条边可以删除，请输出标准输入中最后出现的一条边。
输入示例
3
1 2
1 3
2 3
输出示例
2 3
提示信息

在删除 2 3 后有向图可以变为一棵合法的有向树，所以输出 2 3

这道题的目的是在有向图中找到一条冗余边，该冗余边可以是多余的边或导致图中形成环路的边。具体解决思路是通过并查集和父节点数组相结合，来处理节点的父节点冲突以及环路检测问题。

题解思路

1. 分析图的性质：
   树的性质：一棵树有 n 个节点和 n-1 条边，是一个无环的连通图。
   有向图的情况：给定的图有 n 个节点和 n 条边，多了一条附加的边，因此图可能会出现两种情况：
       · 有一个节点有两个父节点，即一个节点被指向两次。
       · 有环路，即一个节点可以通过有向边回到自己。
2. 解决方法：
   记录每个节点的父节点：使用数组 parent 来记录每个节点的父节点。如果发现某个节点有两个父节点，说明存在冲突（conflict）。
   使用并查集检测环路：通过并查集（Union-Find）来检测是否有环路（cycle）。如果在合并时发现两个节点已经属于同一集合，说明这条边会导致环路。
   根据冲突和环路的情况返回结果：
   如果有冲突但没有环路，那么冲突的边就是冗余边。
   如果同时有冲突和环路，优先返回与环路相关的边。
   如果没有冲突但有环路，返回环路中的最后一条边。

举个栗子

为什么优先删除与环路相关的边？
如果有冲突但没有环路，那么说明其中一条边只是使某个节点有两个父节点，此时直接删除指向该节点的后出现的那条边即可。

但如果同时存在父节点冲突和环路，此时导致问题的根源是环路，因为冗余边不仅让一个节点有两个父节点，还让整个图形成了一个环。优先删除与环路相关的边可以确保解决问题。

假设输入的图如下：

edges = [[1, 2], [2, 3], [3, 4], [4, 2], [1, 5]]

图的结构：

   1/ \2 - 5|3|4|2  <-- 环路

• 父节点冲突：边 [4, 2] 让节点 2 有两个父节点（分别是 1 和 4）。
• 环路：2 → 3 → 4 → 2 形成一个环。

此时，我们要优先删除形成环的那条边，即 [4, 2]，这样可以确保我们既消除了环路，又让图成为一棵树。

因此，在有冲突和环路的情况下，删除环路中的冗余边更能有效解决问题，避免冗余的边继续影响树的结构。

冲突是因为一个节点有多个父节点。
环路是因为多余的边使得整个图不再是树。

代码实现

class UnionFind:def __init__(self, n):# 初始化并查集，每个节点的祖先初始化为自己self.ancestor = list(range(n))# 合并两个节点所在的集合def union(self, index1: int, index2: int):# 找到两个节点的根，并将其中一个根指向另一个根self.ancestor[self.find(index1)] = self.find(index2)# 查找节点的根，同时进行路径压缩def find(self, index: int) -> int:if self.ancestor[index] != index:# 路径压缩，将当前节点的父节点直接指向根self.ancestor[index] = self.find(self.ancestor[index])return self.ancestor[index]class Solution:def findRedundantDirectedConnection(self, edges: list[list[int]]) -> list[int]:n = len(edges)  # 图的节点数uf = UnionFind(n + 1)  # 初始化并查集parent = list(range(n + 1))  # 每个节点的父节点初始化为自己conflict = -1  # 记录冲突边的索引cycle = -1  # 记录环路边的索引# 遍历所有边for i, (node1, node2) in enumerate(edges):if parent[node2] != node2:# 如果 node2 已经有父节点，说明冲突发生，记录这条边conflict = ielse:# 否则，更新 node2 的父节点为 node1parent[node2] = node1# 判断是否形成环路if uf.find(node1) == uf.find(node2):# 如果 node1 和 node2 已经属于同一个集合，说明形成了环路cycle = ielse:# 如果没有形成环路，将 node1 和 node2 合并到同一个集合uf.union(node1, node2)# 如果没有冲突边，返回导致环路的那条边if conflict < 0:return [edges[cycle][0], edges[cycle][1]]else:# 处理冲突边conflictEdge = edges[conflict]if cycle >= 0:# 如果有环路，返回与环路相关的边return [parent[conflictEdge[1]], conflictEdge[1]]else:# 如果没有环路，直接返回冲突边return [conflictEdge[0], conflictEdge[1]]

时间复杂度：

• 查找和合并的均摊时间复杂度为 O(α(n))，其中 α(n) 是反阿克曼函数，近似为常数。
• 遍历所有边的时间复杂度为 O(n)。
• 总体复杂度接近 O(n)。

卡码题目链接
题目文章讲解