期望极大算法(Expectation Maximization Algorithm,EM)
定义
输入:观测变量数据Y,隐变量数据Z,联合分布P(Y,Z| θ \theta θ),条件分布PP(Z,Y| θ \theta θ);
输出:模型参数 θ \theta θ
(1)选择参数的初值 θ ( 0 ) , 开始迭代 ; \theta^{(0)},开始迭代; θ(0),开始迭代;
(2)E步:记 θ ( i ) 为第 i 次迭代参数 \theta^{(i)}为第i次迭代参数 θ(i)为第i次迭代参数\theta 的估计值 , 在第 的估计值,在第 的估计值,在第i+1$次迭代的E步,计算
Q ( θ , θ ( i ) ) = E Z [ l o g P ( Y , Z ∣ θ ) ∣ Y , θ ( i ) ] = ∑ Z l o g P ( Y , Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) Q(\theta,\theta^{(i)}) = E_Z\big[ log P(Y,Z|\theta)|Y,\theta^{(i)} \big] = \sum_{Z}log P(Y,Z|\theta) P(Z|Y,\theta^{(i)}) Q(θ,θ(i))=EZ[logP(Y,Z∣θ)∣Y,θ(i)]=Z∑logP(Y,Z∣θ)P(Z∣Y,θ(i))
P ( Z ∣ Y , θ ( i ) ) P(Z|Y,\theta^{(i)}) P(Z∣Y,θ(i)):给定观测数据 Y Y Y和当前的参数估计 θ ( i ) \theta^{(i)} θ(i)下隐变量数据 Z Z Z的条件概率分布;
(3)M步:求使 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i))极大化的 θ \theta θ,确定第 i + 1 i+1 i+1次迭代的参数的估计值 θ ( i + 1 ) \theta^{(i+1)} θ(i+1)
θ ( i + 1 ) = a r g ∗ m a x θ Q ( θ , θ ( i ) ) \theta^{(i+1)} = arg * \mathop{max}\limits_{\theta} Q(\theta,\theta^{(i)}) θ(i+1)=arg∗θmaxQ(θ,θ(i))
(4)重复第(2)步和第(3)步,直到收敛。
输入空间
T = { ( x 1 , x 2 , … , x N } T=\left\{(x_1,x_2,\dots,x_N\right\} T={(x1,x2,…,xN}
import numpy as np
import random
import math
import timedef loadData(mu0, sigma0, mu1, sigma1, alpha0, alpha1):'''初始化数据集这里通过服从高斯分布的随机函数来生成数据集:param mu0: 高斯0的均值:param sigma0: 高斯0的方差:param mu1: 高斯1的均值:param sigma1: 高斯1的方差:param alpha0: 高斯0的系数:param alpha1: 高斯1的系数:return: 混合了两个高斯分布的数据'''#定义数据集长度为1000length = 1000#初始化第一个高斯分布,生成数据,数据长度为length * alpha系数,以此来#满足alpha的作用data0 = np.random.normal(mu0, sigma0, int(length * alpha0))#第二个高斯分布的数据data1 = np.random.normal(mu1, sigma1, int(length * alpha1))#初始化总数据集#两个高斯分布的数据混合后会放在该数据集中返回dataSet = []#将第一个数据集的内容添加进去dataSet.extend(data0)#添加第二个数据集的数据dataSet.extend(data1)#对总的数据集进行打乱(其实不打乱也没事,只不过打乱一下直观上让人感觉已经混合了# 读者可以将下面这句话屏蔽以后看看效果是否有差别)random.shuffle(dataSet)#返回伪造好的数据集return dataSet
# mu0是均值μ
# sigmod是方差σ
#在设置上两个alpha的和必须为1,其他没有什么具体要求,符合高斯定义就可以
alpha0 = 0.3; mu0 = -2; sigmod0 = 0.5
alpha1 = 0.7; mu1 = 0.5; sigmod1 = 1#初始化数据集
dataSetList = loadData(mu0, sigmod0, mu1, sigmod1, alpha0, alpha1)
np.shape(dataSetList)
print('alpha0:%.1f, mu0:%.1f, sigmod0:%.1f, alpha1:%.1f, mu1:%.1f, sigmod1:%.1f'%(alpha0, mu0, sigmod0, alpha1, mu1, sigmod1))
统计学习方法
模型
a r g ∗ m a x θ Q ( θ , θ ( i ) ) arg * \mathop{max}\limits_{\theta} Q(\theta,\theta^{(i)}) arg∗θmaxQ(θ,θ(i))
策略
L ( θ ) = l o g ( ∑ Z P ( Y ∣ Z , θ ) P ( Z ∣ θ ) ) L(\theta) = log\bigg( \sum_{Z} P(Y|Z,\theta) P(Z|\theta) \bigg) L(θ)=log(Z∑P(Y∣Z,θ)P(Z∣θ))
算法
高斯混合模型
P ( y ∣ θ ) = ∑ k = 1 K α k ϕ ( y ∣ θ k ) , α k : 系数 , α k ≥ 0 , ∑ k = 1 K α k = 1 ; ϕ ( y ∣ θ k ) : 高斯分布密度 , θ k = ( μ k , σ k 2 ) P(y|\theta) = \sum_{k=1}^K \alpha_k \phi(y|\theta_k),\alpha_k:系数,\alpha_k \geq 0,\sum_{k=1}^K \alpha_k = 1;\phi(y|\theta_k):高斯分布密度,\theta_k=(\mu_k,\sigma_k^2) P(y∣θ)=k=1∑Kαkϕ(y∣θk),αk:系数,αk≥0,k=1∑Kαk=1;ϕ(y∣θk):高斯分布密度,θk=(μk,σk2)
ϕ ( y ∣ θ k ) = 1 2 π σ k e x p ( − ( y − μ k ) 2 2 σ k 2 ) \phi(y|\theta_k) = \frac{1}{\sqrt{2\pi}\sigma_k} exp \bigg( - \frac{(y-\mu_k)^2}{2\sigma_k^2} \bigg) ϕ(y∣θk)=2πσk1exp(−2σk2(y−μk)2)
def calcGauss(dataSetArr, mu, sigmod):'''根据高斯密度函数计算值:param dataSetArr: 可观测数据集:param mu: 均值:param sigmod: 方差:return: 整个可观测数据集的高斯分布密度(向量形式)'''result = (1 / (math.sqrt(2 * math.pi) * sigmod)) * \np.exp(-1 * (dataSetArr - mu) * (dataSetArr - mu) / (2 * sigmod**2))#返回结果return result
Q ( θ , θ ( i ) ) = E Z [ l o g P ( Y , Z ∣ θ ) ∣ Y , θ ( i ) ] = ∑ Z l o g P ( Y , Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) Q(\theta,\theta^{(i)}) = E_Z\big[ log P(Y,Z|\theta)|Y,\theta^{(i)} \big] = \sum_{Z}log P(Y,Z|\theta) P(Z|Y,\theta^{(i)}) Q(θ,θ(i))=EZ[logP(Y,Z∣θ)∣Y,θ(i)]=Z∑logP(Y,Z∣θ)P(Z∣Y,θ(i))
P ( Z ∣ Y , θ ( i ) ) : 给定观测数据 Y 和当前的参数估计 θ ( i ) 下隐变量数据 Z 的条件概率分布; P(Z|Y,\theta^{(i)}):给定观测数据Y和当前的参数估计\theta^{(i)}下隐变量数据Z的条件概率分布; P(Z∣Y,θ(i)):给定观测数据Y和当前的参数估计θ(i)下隐变量数据Z的条件概率分布;
def E_step(dataSetArr, alpha0, mu0, sigmod0, alpha1, mu1, sigmod1):'''依据当前模型参数,计算分模型k对观数据y的响应度:param dataSetArr: 可观测数据y:param alpha0: 高斯模型0的系数:param mu0: 高斯模型0的均值:param sigmod0: 高斯模型0的方差:param alpha1: 高斯模型1的系数:param mu1: 高斯模型1的均值:param sigmod1: 高斯模型1的方差:return: 两个模型各自的响应度'''#计算y0的响应度#先计算模型0的响应度的分子gamma0 = alpha0 * calcGauss(dataSetArr, mu0, sigmod0)#模型1响应度的分子gamma1 = alpha1 * calcGauss(dataSetArr, mu1, sigmod1)#两者相加为E步中的分布sum = gamma0 + gamma1#各自相除,得到两个模型的响应度gamma0 = gamma0 / sumgamma1 = gamma1 / sum#返回两个模型响应度return gamma0, gamma1
θ ( i + 1 ) = a r g ∗ m a x θ Q ( θ , θ ( i ) ) \theta^{(i+1)} = arg * \mathop{max}\limits_{\theta} Q(\theta,\theta^{(i)}) θ(i+1)=arg∗θmaxQ(θ,θ(i))
def M_step(muo, mu1, gamma0, gamma1, dataSetArr):mu0_new = np.dot(gamma0, dataSetArr) / np.sum(gamma0)mu1_new = np.dot(gamma1, dataSetArr) / np.sum(gamma1)sigmod0_new = math.sqrt(np.dot(gamma0, (dataSetArr - muo)**2) / np.sum(gamma0))sigmod1_new = math.sqrt(np.dot(gamma1, (dataSetArr - mu1)**2) / np.sum(gamma1))alpha0_new = np.sum(gamma0) / len(gamma0)alpha1_new = np.sum(gamma1) / len(gamma1)#将更新的值返回return mu0_new, mu1_new, sigmod0_new, sigmod1_new, alpha0_new, alpha1_new
def EM_Train(dataSetList, iter = 500):'''根据EM算法进行参数估计:param dataSetList:数据集(可观测数据):param iter: 迭代次数:return: 估计的参数'''#将可观测数据y转换为数组形式,主要是为了方便后续运算dataSetArr = np.array(dataSetList)#步骤1:对参数取初值,开始迭代alpha0 = 0.5; mu0 = 0; sigmod0 = 1alpha1 = 0.5; mu1 = 1; sigmod1 = 1#开始迭代step = 0while (step < iter):#每次进入一次迭代后迭代次数加1step += 1#步骤2:E步:依据当前模型参数,计算分模型k对观测数据y的响应度gamma0, gamma1 = E_step(dataSetArr, alpha0, mu0, sigmod0, alpha1, mu1, sigmod1)#步骤3:M步mu0, mu1, sigmod0, sigmod1, alpha0, alpha1 = \M_step(mu0, mu1, gamma0, gamma1, dataSetArr)#迭代结束后将更新后的各参数返回return alpha0, mu0, sigmod0, alpha1, mu1, sigmod1
alpha0, mu0, sigmod0, alpha1, mu1, sigmod1 = EM_Train(dataSetList)
print('Parameters predict:')
print('alpha0:%.1f, mu0:%.1f, sigmod0:%.1f, alpha1:%.1f, mu1:%.1f, sigmod1:%.1f' % (alpha0, mu0, sigmod0, alpha1, mu1, sigmod1))
假设空间(Hypothesis Space)
{ a r g ∗ m a x θ Q ( θ , θ ( i ) ) } \left\{ arg * \mathop{max}\limits_{\theta} Q(\theta,\theta^{(i)}) \right\} {arg∗θmaxQ(θ,θ(i))}
输出
θ \theta θ
相关文章:
)
期望极大算法(Expectation Maximization Algorithm,EM)
定义 输入:观测变量数据Y,隐变量数据Z,联合分布P(Y,Z| θ \theta θ),条件分布PP(Z,Y| θ \theta θ); 输出:模型参数 θ \theta θ (1)选择参数的初值 θ ( 0 ) , 开始迭代 ; \theta^{(0)},开始迭代; θ(0),开始迭代; (2)E步:记 θ ( i ) 为第 i 次迭代参数 \theta^{(i)}为第…...
初级练习[4]:多表查询——表联结
目录 多表查询:表联结示例 查询有两门以上的课程不及格的同学的学号及其平均成绩 查询所有学生的学号、姓名、选课数、总成绩 查询平均成绩大于85的所有学生的学号、姓名和平均成绩 查询学生的选课情况:学号,姓名,课程号,课程名称 查询出每门课程的及格人数和不及格人数 …...
基于JAVA+SpringBoot+Vue的中药实验管理系统
基于JAVASpringBootVue的中药实验管理系统 前言 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN[新星计划]导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末附源码下载链接🍅 哈…...

移动硬盘读取出错结构损坏?数据恢复实战指南
移动硬盘困境:读取出错与结构损坏 在日常的数据存储与传输中,移动硬盘以其大容量、便携性成为了众多用户的首选。然而,当移动硬盘遭遇读取出错或结构损坏的困境时,那些珍贵的文件、照片、视频等数据便岌岌可危,让人心…...

Web安全之HTTPS调用详解和证书说明案例示范
随着互联网的高速发展,网络安全成为了一个不可忽视的话题,特别是在涉及用户敏感信息的业务系统中。在此背景下,使用HTTPS取代HTTP成为了大势所趋。本文将以电商交易系统为例,详细介绍HTTPS的重要性,并探讨如何通过HTTP…...

man命令学习记录
使用man来查看命令的用法 man ls 想了解Linux命令的用法假设你想查ls命令的更多信息,输入man ls,就会打开man page(man是manual的缩写,因此man page就是“手册页面”),显示关于ls命令各个方面的信息。 通常…...

Linux三剑客-grep
grep介绍 全拼: Global search REgular expression and Print out line. 作用: 文本搜索工具,根据用户指定的“模式(过滤条件)”对目标文本逐行进行匹配检查,打印匹配到的行。 模式: 有正则表达…...

备忘录模式memento
学习笔记,原文链接 https://refactoringguru.cn/design-patterns/memento 允许生成对象状态的快照并在以后将其还原。备忘录不会影响它所处理的对象的内部结构, 也不会影响快照中保存的数据。...

5-【JavaWeb】JUnit 单元测试及JUL 日志系统
1. 使用 JUnit 进行单元测试 JUnit 是 Java 中非常流行的单元测试框架,MyBatis 与 JUnit 可以很好地结合,来测试持久层代码的正确性。 1.1 添加 JUnit 依赖 在使用 JUnit 之前,需要在 pom.xml 中引入 JUnit 依赖。 <dependency><…...

多人开发小程序设置体验版的痛点
抛出痛点 在分配任务时,我们将需求分为三个分支任务,分别由前端A、B、C负责: 前端A: HCC-111-实现登录功能前端B: HCC-112-实现用户注册前端C: HCC-113-实现用户删除 相应地,我们创建三个功能分支: feature_HCC-111-实现登录功能feature_HCC-112-实现用户注册feature_HCC-1…...

【Kubernetes】常见面试题汇总(七)
目录 20.简述 Kubernetes 创建一个 Pod 的主要流程? 21.简述 Kubernetes 中 Pod 的重启策略? 20.简述 Kubernetes 创建一个 Pod 的主要流程? Kubernetes 中创建一个 Pod 涉及多个组件之间联动,主要流程如下: &#…...

EmguCV学习笔记 C# 11.1 DnnInvoke类
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。 EmguCV是一个基于OpenCV的开源免费的跨平台计算机视觉库,它向C#和VB.NET开发者提供了OpenCV库的大部分功能。 教程VB.net版本请访问…...

论文解读 | ACL2024 Outstanding Paper:因果指导的主动学习方法:助力大语言模型自动识别并去除偏见...
点击蓝字 关注我们 AI TIME欢迎每一位AI爱好者的加入! 点击阅读原文观看作者直播讲解回放! 作者简介 孙洲浩,哈尔滨工业大学SCIR实验室博士生 概述 尽管大语言模型(LLMs)展现出了非常强大的能力,但它们仍然…...
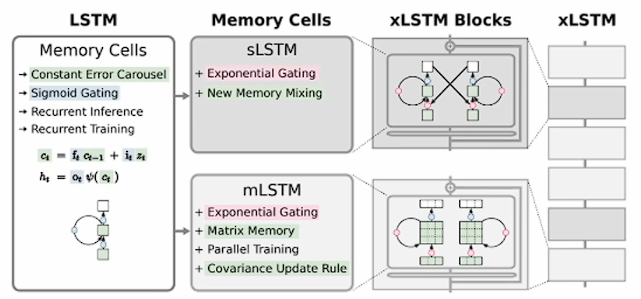
xLSTM模型学习笔记
笔记来源:bilibili LSTM 回顾 原始的 LSTM 是为了解决 RNN 时序反向传播中梯度消失和爆炸问题而提出的。 其所谓的门控机制,其实就是一种时序上的注意力机制,相当于把不同时间进行"掺和",是对时序信息的一种选择性控制…...

woocommerce 调用当前product_tag 为标题
要在 WooCommerce 中调用当前产品标签(product tag)作为标题,你可以使用以下代码。这段代码将获取当前产品标签的名称,并将其显示为标题。 <?php // 获取当前产品标签名称 $current_tag single_term_title(, false);// 检查是…...

音视频开发:基于sdl的pcm播放器
源码 /*** SDL2播放PCM*** 本程序使用SDL2播放PCM音频采样数据。SDL实际上是对底层绘图* API(Direct3D,OpenGL)的封装,使用起来明显简单于直接调用底层* API。* 测试的PCM数据采用采样率44.1k, 采用精度S16SYS, 通道数2** 函数调…...

[产品管理-6]:NPDP新产品开发 - 4 - 战略 - 创新支持战略,支持组织的总体创新战略(平台战略、技术战略、营销战略、知识产权战略、能力建设战略)
目录 一、创新支持战略概述 二、平台战略:大平台小产品战略 2.1 概述 1、平台战略的定义 2、平台战略的特点 3、平台战略的应用领域 4、平台战略的成功案例 5、平台战略的发展趋势 2.2 大平台小产品战略 1)大平台的建设 2)、小产品…...

Cursor:程序员的AI助手,开启智能编程新时代
在当今快节奏的软件开发世界,效率和准确性是成功的关键。而 Cursor,作为一款创新的人工智能编程工具,正在极大地改变着编程的面貌,为开发者带来前所未有的便捷与惊喜。 智能代码生成 Cursor 利用强大的人工智能模型,…...

OpenAI 刚刚发布了新的Sora视频——实现的真人效果令人惊叹
在 YouTube 上发布了两段由专业创作者制作的新的“Sora Showcase”视频。这些视频展示了尚未发布的 Sora AI 视频模型的惊人潜力。 Sora 于今年二月首次宣布,但由于生成时间、成本和错误信息的潜在风险,光年AI 仅向一小部分创作者 开放了该模型。 自So…...

计算机视觉学习路线
计算机视觉是一门让机器理解和解释视觉世界的科学,它涉及到图像识别、图像处理、模式识别等多个方向。学习计算机视觉的路线通常包括以下几个阶段: 数学和编程基础:需要掌握微积分、线性代数、概率论等数学知识,以及Python或C等编…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...
