当前位置： 首页 > news >正文

告别植物神经紊乱，这5种运动让你身心平衡，活力满满！‍♀️✨

news 2026/2/9 1:23:32

Hey小伙伴们~👋 最近是不是感觉压力山大，晚上辗转反侧，白天又无精打采？😴😔 这可能是植物神经紊乱在悄悄作祟哦！别怕，今天就来给大家种草几个超有效的运动方式，帮你找回那个元气满满的自己！💪✨

1. ‌深呼吸瑜伽‌ 🧘‍♀️

首先登场的是我们的心灵导师——深呼吸瑜伽！找个安静的地方，铺开你的瑜伽垫，随着轻柔的音乐，慢慢吸气到腹部，再缓缓呼出。每一个呼吸都是对身心的温柔抚慰，能有效缓解紧张情绪，平衡植物神经。🌬️💖

2. ‌慢跑解压‌ 🏃‍♀️

穿上跑鞋，迎着晨光或晚霞，来一场说走就走的慢跑吧！慢跑不仅能促进血液循环，增强心肺功能，更重要的是，它能让你在运动中释放压力，找回内心的平静。记得，不必追求速度，享受过程最重要！🏃‍♂️🌈

3. ‌游泳放松‌ 🏊‍♀️

如果你喜欢水，那么游泳绝对是你的不二之选！水的浮力能减轻身体负担，同时全身肌肉在水中的均匀运动，能有效缓解肌肉紧张，对改善植物神经紊乱有奇效。而且，游泳还是一项低冲击运动，适合各种体质的小伙伴哦！🌊💪

4. ‌太极养生‌ 🧘‍♂️

太极，这门古老的养生艺术，讲究的是内外兼修，动静结合。通过缓慢而连贯的动作，配合深呼吸，太极能够调和气血，平衡阴阳，对改善植物神经紊乱有着不可小觑的作用。每天几分钟，让你感受到身心的和谐统一。🌿💫

5. ‌舞蹈释放‌ 💃

最后，来一场说走就走的舞蹈吧！无论是街舞、爵士还是拉丁，随着音乐的节奏摇摆，让身体自由表达，所有的烦恼和压力都会随着汗水一起流走。舞蹈不仅能锻炼身体的协调性，更能激发内心的快乐因子，让你重拾生活的乐趣！🎵💃

小伙伴们，记得哦，运动是治愈一切不开心的良药！💊 但别忘了，持之以恒才是关键。选择一项或几项你喜欢的运动，坚持下去，相信不久的将来，你会发现自己变得更加自信、健康、有活力！💪🌟

相关文章：

告别植物神经紊乱，这5种运动让你身心平衡，活力满满！‍♀️✨

Hey小伙伴们~👋 最近是不是感觉压力山大，晚上辗转反侧，白天又无精打采？😴😔 这可能是植物神经紊乱在悄悄作祟哦！别怕，今天就来给大家种草几个超有效的运动方式，帮你找回那…...

编程日记 2024/9/12 12:21:26

又一个iPhone时代开始

今年的苹果秋季发布会在昨晚召开了，今天早上我们也看到了很多相关的新闻。我猜你看完后的感觉可能是，这不过又是一次普普通通的参数升级。又是提升了百分之多少，又是增加了多少倍——非常简单的一些更新。比如说芯片升级了、相机的摄像头一会…...

编程日记 2024/9/12 12:19:24

在 CentOS 中永久关闭防火墙的步骤

在 CentOS 中永久关闭防火墙的步骤 在 CentOS 系统中，防火墙通常由 firewalld 服务管理。如果你希望在系统中永久关闭防火墙，可以按照以下步骤操作： 1. 停止防火墙服务 首先，你需要停止当前正在运行的防火墙服务。可以使用以下…...

编程日记 2024/9/12 12:18:23

【数据库】详解基本SQL语句用法

一、SELECTING DATA FROM TABLES【查询数据】 SELECT命令是表上所有查询的基础，因此给出它的完整描述以显示它的功能。在描述之后提供各种格式的示例。 1.1 整体描述 SELECT column1, column2, ... FROMtable1 [INNER | LEFT | RIGHT] JOIN table2 on conditions…...

编程日记 2024/9/12 12:17:22

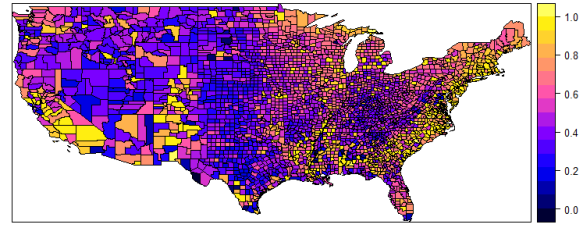
R语言地理加权回归、主成份分析、判别分析等空间异质性数据分析

在自然和社会科学领域有大量与地理或空间有关的数据，这一类数据一般具有严重的空间异质性，而通常的统计学方法并不能处理空间异质性，因而对此类型的数据无能为力。以地理加权回归为基础的一系列方法：经典地理加权回归，…...

编程日记 2024/9/12 12:16:21

数学建模笔记—— 非线性规划

数学建模笔记—— 非线性规划 非线性规划1. 模型原理1.1 非线性规划的标准型1.2 非线性规划求解的Matlab函数 2. 典型例题3. matlab代码求解3.1 例1 一个简单示例3.2 例2 选址问题1. 第一问 线性规划2. 第二问 非线性规划 非线性规划 非线性规划是一种求解目标函数或约束条件中…...

编程日记 2024/9/12 12:13:18

JavaScript中的控制流语句：break、continue、return、throw

在JavaScript编程中，控制流语句是控制代码执行流程的重要工具。这些语句包括break、continue、return和throw，它们可以在循环、函数以及其他代码块中使用，以改变正常的执行顺序。下面我们将逐一探讨这些语句的用途和示例。 break break语句…...

编程日记 2024/9/12 12:12:16

移动通信为啥要用双极化天线？

❝本文简单介绍下移动通信为啥要用双极化天线及其简单概述。 移动通信为啥要用双极化天线？ - RFASK射频问问❝本文简单介绍下移动通信为啥要用双极化天线及其简单概述。什么是极化？电磁波的极化通常是用其电场矢量的空间指向来描述：在空间某…...

编程日记 2024/9/12 12:10:15

C语言从头学59——学习头文件math.h（二）

继续学习头文件<math.h>&#xff0c;编号接续前文。 六、三角函数 math.h中的三角函数包括&#xff1a; acos()&#xff1a;反余弦&#xff0c;参数范围-1至1&#xff0c;返回值double类型&#xff1a;0~PI asin()&#xff1a;反正弦&#xff0c;参…...

编程日记 2024/9/12 12:08:13

Leetcode 3283. Maximum Number of Moves to Kill All Pawns

Leetcode 3283. Maximum Number of Moves to Kill All Pawns 1. 解题思路2. 代码实现 题目链接&#xff1a;3283. Maximum Number of Moves to Kill All Pawns 1. 解题思路 这一题坦率地说没有想到什么好的思路&#xff0c;因此只能非常暴力地按照题意进行了一下构造。 显然…...

编程日记 2024/9/12 12:07:12

智能物流新“黑神话”：各位“天命人”，这份行业应用锦集请收下！

全球工业革新浪潮中&#xff0c;智能物流正成为制造业转型升级的核心驱动力之一。高柔性的智能物流解决方案可以帮助企业应对复杂的物流挑战&#xff0c;实现生产到仓储全过程的智能化、柔性化和高度集成&#xff0c;带来显著的经济效益。 作为行业领先的全场景柔性物流综合解…...

编程日记 2024/9/12 12:03:08

SpringSecurity原理解析（五）：HttpSecurity 类处理流程

1、SpringSecurity 在spring boot中与SSM项目中基于配置文件的区别 通过前边的笔记我们可以知道&#xff0c;在传统的SSM项目中 SpringSecurity的使用是基于配置文件 的&#xff0c;然后spring 容器初始化的时候将 SpringSecurity 中的各种标签解析成对应的Bean对象&#xff0c…...

编程日记 2024/9/12 12:02:06

C++系列-匿名对象

匿名对象 &#x1f4a2;什么是匿名对象&#x1f4a2;匿名对象的创建方式及作用域&#x1f4a2;匿名对象的对象类型&#x1f4a2;&#x1f4a2;匿名的基本数据类型对象&#x1f4a2;&#x1f4a2;匿名的自定义的类类型对象&#x1f4a2;&#x1f4a2;匿名的标准库的类对象 &…...

编程日记 2024/9/12 12:01:04

tofixed和math.round什么区别

1、floor 返回不大于的最大整数&#xff08;向下取整&#xff09; 2、round 则是4舍5入的计算&#xff0c;入的时候是到大于它的整数&#xff08;当-1.5时可见&#xff0c;四舍五入后得到的结果不是我们期待的&#xff0c;解决办法是先对他取绝对值&#xff0c;然后在用round方…...

编程日记 2024/9/12 11:56:59

OPENAIGC开发者大赛高校组金奖 | 基于混合大语言模型与多模态的全过程通用AI Agent

在第二届拯救者杯OPENAIGC开发者大赛中&#xff0c;涌现出一批技术突出、创意卓越的作品。为了让这些优秀项目被更多人看到&#xff0c;我们特意开设了优秀作品报道专栏&#xff0c;旨在展示其独特之处和开发者的精彩故事。 无论您是技术专家还是爱好者&#xff0c;希望能带给您…...

编程日记 2024/9/12 11:55:58

MySql批量迁移数据库

导出数据库 将指定数据库实例&#xff08;MYSQL_HOST、MYSQL_PORT、MYSQL_USER、MYSQL_PASSWORD&#xff09;中的所有数据库&#xff08;表结构、数据&#xff09;导出到指定目录&#xff08;BACKUP_DIR&#xff09;下的多个单独的SQL脚本&#xff0c;每个SQL脚本名称即为数据…...

编程日记 2024/9/12 11:53:56

一、selenium自动化简介selenium工具集

文章目录 一、简介二、组成部分三、selenium工具集3.1 Selenium IDE3.2 Selenium WebDriver3.3 Selenium Grid3.4 Appium 一、简介 官方网站 Selenium 是支持 web 浏览器自动化的一系列工具和库的综合项目。 它提供了扩展来模拟用户与浏览器的交互&#xff0c;用于扩展浏览器分…...

编程日记 2024/9/12 11:52:56

CCF推荐B类会议和期刊总结：（计算机网络领域）

CCF推荐B类会议和期刊总结&#xff08;计算机网络领域&#xff09; 在计算机网络领域&#xff0c;中国计算机学会&#xff08;CCF&#xff09;推荐的B类会议和期刊代表了该领域的较高水平。以下是对所有B类会议和期刊的总结&#xff0c;包括全称、出版社、dblp文献网址以及所属…...

编程日记 2024/9/12 11:51:55

[Web安全 网络安全]-文件包含漏洞

文章目录&#xff1a; 一&#xff1a;前言 1.什么是文件包含漏洞 2.文件包含漏洞的成因 3.文件包含漏洞的分类 4.文件包含漏洞的防御策略 5.文件包含函数&#xff08;触发点Sink&#xff09; 6.环境 6.1 靶场 6.2 其他工具 二&#xff1a;文件包含LFI labs靶场实验…...

编程日记 2024/9/12 11:50:54

使用soui4实现一个拾色器

拾色器类 #pragma once class CClrPickerCtrl : public SWindow {DEF_SOBJECT(SWindow, L"clrpicker") public:CClrPickerCtrl(void);~CClrPickerCtrl(void);//跟solider控件设置色调void SetSliderPos(int nPos);//获取选取位置的颜色COLORREF GetColor(); protect…...

编程日记 2024/9/12 11:49:52

大话软工笔记—需求分析概述

需求分析&#xff0c;就是要对需求调研收集到的资料信息逐个地进行拆分、研究&#xff0c;从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要&#xff0c;后续设计的依据主要来自于需求分析的成果&#xff0c;包括: 项目的目的…...

编程新知 2026/1/28 10:58:50

【OSG学习笔记】Day 18: 碰撞检测与物理交互

物理引擎&#xff08;Physics Engine&#xff09; 物理引擎 是一种通过计算机模拟物理规律&#xff08;如力学、碰撞、重力、流体动力学等&#xff09;的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互&#xff0c;广泛应用于 游戏开发、动画制作、虚…...

编程新知 2026/2/4 2:08:30

React19源码系列之 事件插件系统

事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

编程新知 2026/2/7 8:31:55

论文解读：交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架（一）

宇树机器人多姿态起立控制强化学习框架论文解析 论文解读&#xff1a;交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架&#xff08;一&#xff09; 论文解读&#xff1a;交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

编程新知 2025/8/27 0:58:09

浅谈不同二分算法的查找情况

二分算法原理比较简单&#xff0c;但是实际的算法模板却有很多&#xff0c;这一切都源于二分查找问题中的复杂情况和二分算法的边界处理&#xff0c;以下是博主对一些二分算法查找的情况分析。 需要说明的是&#xff0c;以下二分算法都是基于有序序列为升序有序的情况&#xf…...

编程新知 2025/9/14 7:37:32

从 GreenPlum 到镜舟数据库：杭银消费金融湖仓一体转型实践

作者&#xff1a;吴岐诗&#xff0c;杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言&#xff1a;融合数据湖与数仓的创新之路 在数字金融时代&#xff0c;数据已成为金融机构的核心竞争力。杭银消费金…...

编程新知 2026/1/31 12:30:32

探索Selenium：自动化测试的神奇钥匙

目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

编程新知 2025/11/19 18:06:51

c++第七天 继承与派生2

这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分&#xff1a;派生类构造函数与析构函数 当创建一个派生类对象时&#xff0c;基类成员是如何初始化的&#xff1f; 1.当派生类对象创建的时候&#xff0c;基类成员的初始化顺序 …...

编程新知 2026/2/2 21:55:02

uniapp 集成腾讯云 IM 富媒体消息（地理位置/文件）

UniApp 集成腾讯云 IM 富媒体消息全攻略&#xff08;地理位置/文件&#xff09; 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型&#xff0c;核心实现方式&#xff1a; 标准消息类型&#xff1a;直接使用 SDK 内置类型&#xff08;文件、图片等&#xff09;自…...

编程新知 2025/10/25 5:53:05

数据结构：递归的种类（Types of Recursion）

目录 尾递归&#xff08;Tail Recursion&#xff09; 什么是 Loop&#xff08;循环&#xff09;&#xff1f; 复杂度分析 头递归&#xff08;Head Recursion&#xff09; 树形递归&#xff08;Tree Recursion&#xff09; 线性递归&#xff08;Linear Recursion&#xff09;…...

编程新知 2026/2/7 2:25:07