MATLAB-基于高斯过程回归GPR的数据回归预测
目录
目录
1 介绍
1. 1 高斯过程的基本概念
1.2 核函数(协方差函数)
1.3 GPR 的优点
1.4. GPR 的局限
2 运行结果
3 核心代码
1 介绍
高斯过程回归(Gaussian Process Regression, GPR)是一种强大的非参数贝叶斯方法,用于回归和预测任务。GPR 通过假设目标函数服从一个高斯过程(GP),来对未知数据点的分布进行建模,并通过观察数据推断新的预测值。以下是 GPR 的原理解释:
1. 1 高斯过程的基本概念
高斯过程是随机变量的集合,其中任何有限子集的分布都是多元高斯分布。可以将它视为对函数的分布假设,其中每个点的输出(即目标值)都服从一个高斯分布。
1.2 核函数(协方差函数)
核函数 k(x,x′) 是 GPR 的核心,定义了输入点之间的相似性和依赖关系。常见的核函数包括:
-
平方指数核函数(Squared Exponential Kernel): 适用于平滑、连续的函数建模。
1.3 GPR 的优点
- 非参数方法:GPR 不需要预定义特定的函数形式,它根据数据自动调整模型的复杂度。
- 不确定性估计:GPR 不仅提供预测值,还能估计预测的置信区间(通过方差估计)。
- 灵活性:通过选择合适的核函数,GPR 可以适应不同的函数特性(如平滑、周期性等)。
1.4. GPR 的局限
- 计算复杂度高:GPR 的训练涉及核矩阵的求逆,其计算复杂度是 O(n3)\mathcal{O}(n^3)O(n3)(nnn 为样本数量),这使得它在处理大规模数据时较慢。
- 模型选择依赖核函数:核函数的选择对模型的效果有很大的影响,选择不当可能导致模型表现不佳。
2 运行结果

3 核心代码
%% 清空环境变量
warning off % 关闭报警信息
close all % 关闭开启的图窗
clear % 清空变量
clc % 清空命令行%% 导入数据
P_train = xlsread('data')';
T_train= xlsread('data')';
% 测试集——44个样本
P_test=xlsread('data','test set','B2:G45')';
T_test=xlsread('data','test set','H2:H45')';f_ =size(P_train, 1); %输入特征维度
M = size(P_train, 2);
N = size(P_test, 2);
%% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);%% 转置以适应模型
p_train = p_train'; p_test = p_test';
t_train = t_train'; t_test = t_test';相关文章:

MATLAB-基于高斯过程回归GPR的数据回归预测
目录 目录 1 介绍 1. 1 高斯过程的基本概念 1.2 核函数(协方差函数) 1.3 GPR 的优点 1.4. GPR 的局限 2 运行结果 3 核心代码 1 介绍 高斯过程回归(Gaussian Process Regression, GPR)是一种强大的非参数贝叶斯方法&…...

欧洲国际眼科盛会,中国眼科专家周进斩获六项屈光大奖
2024年第42届欧洲白内障和屈光外科医生协会(ESCRS)大会由世界青光眼协会(WGA)、欧洲白内障和屈光外科医生协会(ESCRS)主办,于2024年9月6日至10日在西班牙巴塞罗那举行。 这场眼科盛会,汇聚了来自全球130多个国家的上万名眼科医学领域的顶尖专家、学者和临…...
用户管理(2)创建普通用户)
MySQL——数据库的高级操作(二)用户管理(2)创建普通用户
在创建新用户之前,可以通过 SELECT 语句查看 mysql.user 表中有哪些用户,查询结果如下: mysql> USE mysql; Database changed mysql> SELECT Host, User, authentication_string FROM mysql.user; ----------------------------------…...

VIT论文阅读
把图片看成一个个16x16的patch堆起来的 摘要 卷积神经网络不是必备的,一个纯transformer表现也是非常好的 transformer?2500天tpu v3 介绍 大规模上预训练,小规模任务数据集上微调。扩大模型时候还没观察到瓶颈(还没出现过拟合…...

Python编程入门必备:def关键字与函数参数
在Python编程中,函数是组织代码、实现代码复用和模块化的基础单元。通过函数,可以将复杂的操作封装成独立的代码块,提高代码的可读性和维护性。本文将详细介绍Python中函数的定义和使用,包括def关键字、函数参数的各种类型以及函数…...
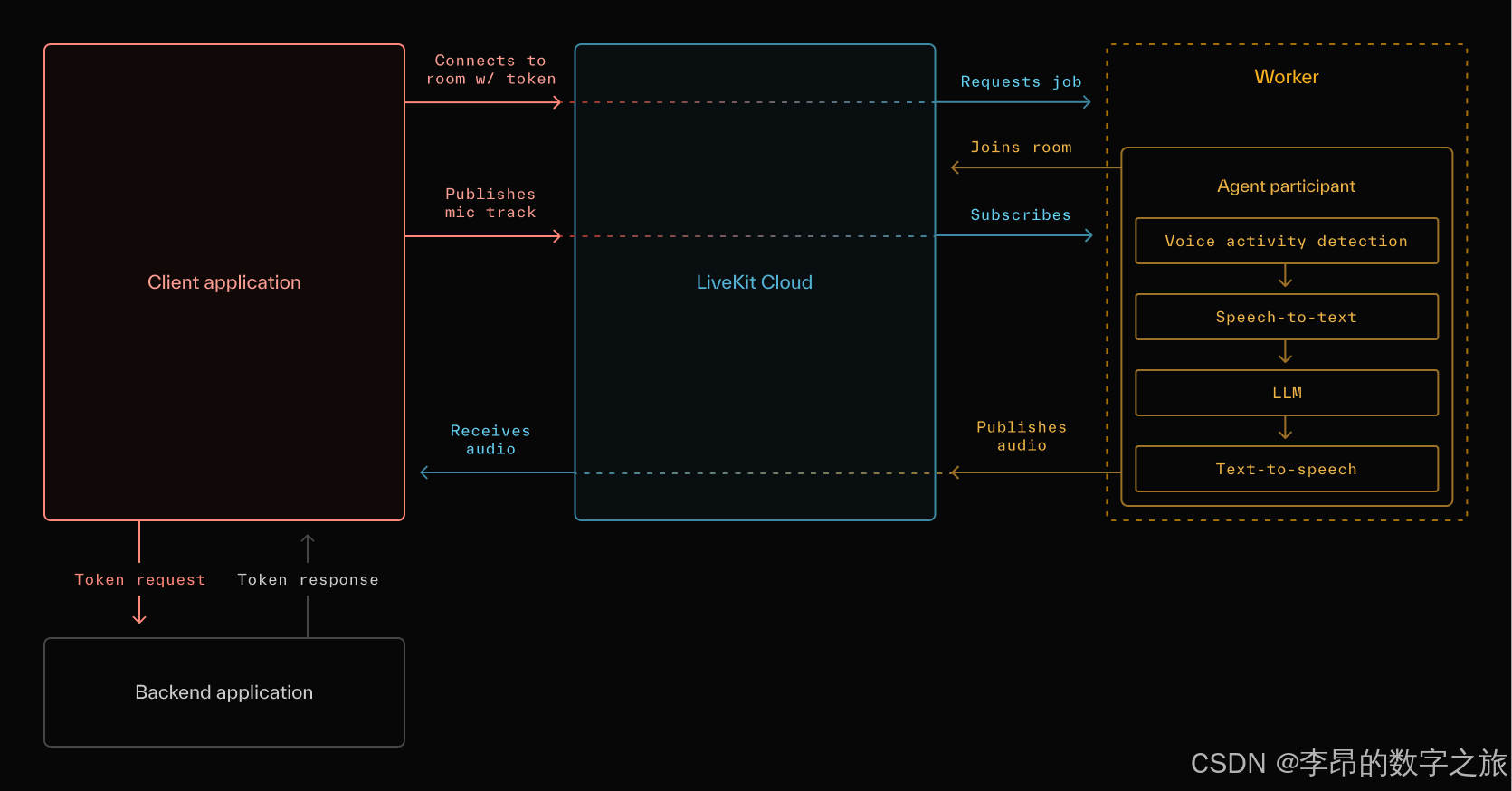
LiveKit的agent介绍
概念 LiveKit核心概念: Room(房间)Participant(参会人)Track(信息流追踪) Agent 架构图 订阅信息流 agent交互流程 客户端操作 加入房间 房间创建方式 手动 赋予用户创建房间的…...

青龙面板 升级 及其 依赖更新修复 检测and日志删除等
青龙版本升级 先关闭服务 cd qinglong目录 docker-compose down 关闭 docker pull whyour/qinglong:版本号 //版本号自行选择,如果是为了修复错误,建议版本微升,不然就直接latest 启动 docker-compose up -d 进入容器࿰…...
)
坐牢第三十七天(Qt)
作业: 使用qt做一个闹钟 widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QPixmap> #include <QBitmap> #include <QLabel> //标签类 #include <QLineEdit> //行编辑器类 #include <QPushBu…...

Vidu 全球首发「主体参照」新功能,一键同步角色特征;GPT-4o 实时音频项目负责人离职创业丨 RTE 开发者日报
开发者朋友们大家好: 这里是 「RTE 开发者日报」 ,每天和大家一起看新闻、聊八卦。我们的社区编辑团队会整理分享 RTE(Real-Time Engagement) 领域内「有话题的新闻」、「有态度的观点」、「有意思的数据」、「有思考的文章」、「…...

电子地图的主要功能与应用
电子地图,即数字地图,是利用计算机技术,以数字方式存储和查阅的地图。它不仅继承了传统纸质地图的基本功能,还通过现代科技手段实现了诸多创新应用。以下是电子地图的主要功能与应用: 一、主要功能 快速存取与显示&…...

基于Java+SpringBoot+Vue+MySQL的西安旅游管理系统网站
作者:计算机学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI等,“文末源码”。 专栏推荐:前后端分离项目源码、SpringBoot项目源码、SSM项目源码 系统展示 基于SpringBootVue的西安旅游管理系统网站【附源码文档】、…...
架构“安培架构“)
简单介绍 NVIDIA推出的图形处理单元(GPU)架构“安培架构“
概念 "安培架构"(Ampere Architecture)是 NVIDIA 推出的一款图形处理单元(GPU)架构,它是继图灵架构之后的下一代产品。安培架构最初在2020年发布,以其高性能和高效率而闻名,广泛应用…...

Qiskit:量子计算的Python工具包
Qiskit是由IBM开发的开源量子计算软件开发工具包,它提供了一套完整的工具,用于量子电路的设计、模拟、优化和执行。Qiskit支持量子算法的开发,并且可以与IBM的量子计算机硬件进行交互。 Qiskit的主要特点 量子电路设计:Qiskit允…...

Python——贪吃蛇
以下是一个简单的贪吃蛇游戏的Python代码示例: import pygame import time import random# 初始化 Pygame pygame.init()# 定义颜色 BLACK (0, 0, 0) WHITE (255, 255, 255) RED (255, 0, 0) GREEN (0, 255, 0) BLUE (0, 0, 255)# 设置屏幕尺寸 screen_width …...
)
WPF 依赖属性与附加属性(面试长问)
在WPF中,**依赖属性(Dependency Property)和附加属性(Attached Property)**是WPF依赖属性系统的重要组成部分。它们虽然都基于依赖属性系统,但用途、定义方式和使用场景有显著差异。以下是两者的详细解释及…...

Python 中的各括号用法
括号的使用 在Python中,括号和中括号有不同的用途: 圆括号 (): 函数调用:当你调用一个函数时,需要使用圆括号,即使没有参数。print("Hello, World!") # 调用print函数表达式分组:在…...

业务流程建模(BPM)的重要性及其应用
什么是业务流程建模(BPM)? 业务流程建模(BPM)是对企业内各项业务流程进行图形化描述的一种方法。它旨在通过可视化的方式帮助企业理解和分析现有的业务流程,从而发现潜在的问题并进行改进。BPM通常采用流程…...

isxdigit函数讲解 <ctype.h>头文件函数
目录 1.头文件 2.isxdigit函数使用 方源一把抓住VS2022,顷刻 炼化! 1.头文件 以上函数都需要包括头文件<ctype.h> ,其中包括 isxdigit 函数 #include<ctype.h> 2.isxdigit函数使用 isxdigit 函数是判断字符是否为十六进制数…...

Linux中安装NextCloud
切换为 root 账号 Ubutu 系统默认登录的用户为非 root 权限用户,为了能正常安装 nextCloud,需要切换为 root 账号。执行如下命令即可: sudo su 更新及安装基础包 请依次运行如下命令,有遇到询问的Is this ok [y/d/N]的时候直接键…...

【编程基础知识】什么是数据库事务
事务(Transaction)是数据库管理系统中的一个基本概念,用于确保数据库操作的原子性(Atomicity)、一致性(Consistency)、隔离性(Isolation)和持久性(Durability…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
