STM32常用数据采集滤波算法
例如,STM32进行滤波处理时,主要目的是处理数据采集过程中可能产生的噪声和尖刺信号。这些噪声可能来自电源干扰、传感器自身的不稳定性或其他外部因素。
1.一阶互补滤波
方法:取a=0~1,本次滤波结果=(1-a)本次采样值+a上次滤波结果 优点:对周期性干扰具有良好的抑制作用适用于波动频率较高的场合 缺点:相位滞后,灵敏度低滞后程度取决于a值大小不能消除滤波频率高于采样频率的1/2的干扰信号。
int firstOrderFilter(int newValue, int oldValue, float a)
{return a * newValue + (1-a) * oldValue;
}
2.中位值滤波
方法:连续采样N次(N取奇数)把N次采样值按大小排列取中间值为本次有效值 优点:能有效克服因偶然因素引起的波动干扰;对温度、液位等变化缓慢的被测参数有良好的滤波效果 缺点:对流量,速度等快速变化的参数不宜。
//中值滤波算法
int middleValueFilter(int N)
{int value_buf[N];int i,j,k,temp;for( i = 0; i < N; ++i){value_buf[i] = HAL_ADC_GetValue(&hadc1); }for(j = 0 ; j < N-1; ++j){for(k = 0; k < N-j-1; ++k){//从小到大排序,冒泡法排序if(value_buf[k] > value_buf[k+1]){temp = value_buf[k];value_buf[k] = value_buf[k+1];value_buf[k+1] = temp;}}}return value_buf[(N-1)/2];
}
3.算术平均滤波
方法:连续取N个采样值进行算术平均运算; N值较大时:信号平滑度较高,但灵敏度较低 N值较小时:信号平滑度较低,但灵敏度较高 N值的选取:一般流量,N=12;压力:N=4 优点:试用于对一般具有随机干扰的信号进行滤波。这种信号的特点是有一个平均值,信号在某一数值范围附近上下波动。 缺点:测量速度较慢或要求数据计算较快的实时控制不适用。
int averageFilter(int N)
{int sum = 0;short i;for(i = 0; i < N; ++i){sum += HAL_ADC_GetValue(&hadc1); }return sum/N;
}
4.滑动平均滤波
方法:把连续取N个采样值看成一个队列,队列的长度固定为N。每次采样到一个新数据放入队尾,并扔掉原来队首的一次数据(先进先出原则)。把队列中的N个数据进行算术平均运算,就可获得新的滤波结果。 N值的选取:流量,N=12;压力:N=4;液面,N=4~12;温度,N=1~4 优点:对周期性干扰有良好的抑制作用,平滑度高;试用于高频振荡的系统 缺点:灵敏度低;对偶然出现的脉冲性干扰的抑制作用较差,不适于脉冲干扰较严重的场合 比较浪费RAM(改进方法,减去的不是队首的值,而是上一次得到的平均值)
//平滑均值滤波
#define N 10
int value_buf[N];
int sum=0;
int curNum=0;
int moveAverageFilter()
{if(curNum < N){value_buf[curNum] = HAL_ADC_GetValue(&hadc1);sum += value_buf[curNum];curNum++;return sum/curNum;}else{sum -= sum/N;sum += HAL_ADC_GetValue(&hadc1);return sum/N;}
}
5.限幅平均滤波
方法:相当于“限幅滤波法”+“递推平均滤波法” 每次采样到的新数据先进行限幅处理再送入队列进行递推平均滤波处理 优点:对于偶然出现的脉冲性干扰,可消除有其引起的采样值偏差。 缺点:比较浪费RAM
//限幅平均滤波
#define A 50 //限制幅度阈值
#define M 12
int data[M];
int First_flag=0;
int LAverageFilter()
{int i;int temp,sum,flag=0;data[0]=HAL_ADC_GetValue(&hadc1);for(i=1;i<M;i++){temp=HAL_ADC_GetValue(&hadc1);if((temp-data[i-1])>A||((data[i-1]-temp)>A)){i--;flag++;}else{data[i]=temp;}}for(i=0;i<M;i++){sum+=data[i];} return sum/M;
}6.卡尔曼滤波
核心思想:根据当前的仪器"测量值" 和上一刻的 “预测量” 和 “误差”,计算得到当前的最优量,再预测下一刻的量。里面比较突出的是观点是:把误差纳入计算,而且分为预测误差和测量误差两种,通称为噪声。还有一个非常大的特点是:误差独立存在,始终不受测量数据的影响。
优点:巧妙的融合了观测数据与估计数据,对误差进行闭环管理,将误差限定在一定范围。适用性范围很广,时效性和效果都很优秀。
缺点:需要调参,参数的大小对滤波的效果影响较大。
//卡尔曼滤波
int KalmanFilter(int inData)
{static float prevData = 0; //先前数值 上一次滤波后的数据,作为下一次滤波的初始值static float p = 10, q = 0.001, r = 0.001, kGain = 0; // q控制误差 r控制响应速度 //更新估计误差方差p = p + q;//计算卡尔曼增益kGain = p / ( p + r ); //计算本次滤波估计值inData = prevData + ( kGain * ( inData - prevData ) ); //更新测量方差p = ( 1 - kGain ) * p; prevData = inData;return inData; //返回滤波值
}
prevData:保存上一次滤波后的数据,用于下一次的滤波。 p:估计误差方差,表示当前估计值的不确定性。 q:过程噪声方差,表示系统模型的不确定性。 r:测量噪声方差,表示测量数据的不确定性。 kGain:卡尔曼增益,决定了测量数据和估计数据对当前状态估计的影响程度。
初始化静态变量
更新估计误差方差
计算卡尔曼增益
更新估计值
更新估计误差方差
保存当前估计值
返回滤波后的值
7.限幅滤波
核心思想:根据经验判断,确定两次采样允许的最大偏差值(设为A),每次检测到新值时判断: 如果本次值与上次值之差<=A,则本次值有效,如果本次值与上次值之差>A,则本次值无效,放弃本次值,用上次值代替本次值。 优点:能克服偶然因素引起的脉冲干扰 缺点:无法抑制周期性的干扰,平滑度差
#define A 51
u16 Value1;u16 filter1()
{u16 NewValue;Value1 = ftable[b-1];NewValue = ftable[b];b++;a++;if(a==255) a=0;if(b==255) b=1;if(((NewValue - Value1) > A) || ((Value1 - NewValue) > A)){print_host(ftable[a],NewValue);return NewValue;}else{print_host(ftable[a],Value1);return Value1;}
}8.加权递推平均滤波
核心思想: 是对递推平均滤波法的改进,即不同时刻的数据加以不同的权;通常是,越接近现时刻的数据,权取得越大,给予新采样值的权系数越大,则灵敏度越高,但信号平滑度越低。 优点: 适用于有较大纯滞后时间常数的对象,和采样周期较短的系统。 缺点: 对于纯滞后时间常数较小、采样周期较长、变化缓慢的信号;不能迅速反应系统当前所受干扰的严重程度,滤波效果差。
#define FILTER8_N 12
int coe[FILTER8_N] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}; // 加权系数表
int sum_coe = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12; // 加权系数和
int filter_buf[FILTER8_N + 1];
int filter8()
{int i;int filter_sum = 0;filter_buf[FILTER8_N] = ftable[a]; a++;if(a==255) a=0;for(i = 0; i < FILTER8_N; i++) {filter_buf[i] = filter_buf[i + 1]; // 所有数据左移,低位仍掉filter_sum += filter_buf[i] * coe[i];}filter_sum /= sum_coe;
// printf("%d\n",filter_sum);return filter_sum;
}void pros8(void)
{u16 i=0;for(i=0;i<255;i++){print_host(ftable[i],filter8());}
}9.消抖滤波
方法: 设置一个滤波计数器,将每次采样值与当前有效值比较: 如果采样值=当前有效值,则计数器清零; 如果采样值<>当前有效值,则计数器+1,并判断计数器是否>=上限N(溢出); 如果计数器溢出,则将本次值替换当前有效值,并清计数器。 优点: 对于变化缓慢的被测参数有较好的滤波效果; 可避免在临界值附近控制器的反复开/关跳动或显示器上数值抖动。 缺点: 对于快速变化的参数不宜; 如果在计数器溢出的那一次采样到的值恰好是干扰值,则会将干扰值当作有效值导入系统。
#define FILTER9_N 51
u16 i = 0;
u16 Value;
u16 filter9()
{int new_value;Value = ftable[b-1];new_value = ftable[b]; b++;if(b==255) b=1;if(Value != new_value) {i++;if(i > FILTER9_N) {i = 0;Value = new_value;}}else i = 0;return Value;
}void pros9(void)
{u16 i=0;for(i=0;i<255;i++){print_host(ftable[i],filter9());}
}相关文章:

STM32常用数据采集滤波算法
例如,STM32进行滤波处理时,主要目的是处理数据采集过程中可能产生的噪声和尖刺信号。这些噪声可能来自电源干扰、传感器自身的不稳定性或其他外部因素。 1.一阶互补滤波 方法:取a0~1,本次滤波结果(1-a)本次采样值a上…...
9/12)
二分系列(二分查找)9/12
一、分情况讨论 1.左闭右闭:[left,right] 因为是左闭右闭,所以left和right都能直接取到。 #这里将>放到一起,当nums[mid]>target的时候, 要更新右边界,rightmid-1,这样就把一些相同的情况也切出去了 可以理解为找的第一个…...

如何通过可视化大屏,助力智慧城市的“城市微脑”建设?
在智慧城市的宏伟蓝图中,常常面临着一个关键挑战:如何确保这些理念和技术能够真正地惠及城市的每一个角落,每一个产业,以及每一位市民。问题的核心在于城市的具体应用场景,无论是横向的社区、园区、镇街、学校、酒店、…...

何时空仓库
某仓库现存货物 s 箱,每天上午出货 m 箱、下午进货 n 箱,若s≥m>n≥0,则第 k 天将会出现空仓的情况。请你帮仓库管理员编写程序,输入s、m 和 n,计算并输出 k。 输入格式 s,m,n (s≥m>n≥0) 输出格式 k 输入样例…...

美创获评CNVD年度原创漏洞发现贡献单位!
9月10日,第21届中国网络安全年会暨网络安全协同治理分论坛在广州成功举办。会上,美创科技首次获评“CNVD年度原创漏洞发现贡献单位”。 美创科技依托第59号安全实验室,专注数据安全技术和攻防研究。凭借深厚的技术积累与优势,被遴…...

Spring 循环依赖原理及解决方案
一、什么是循环依赖 循环依赖指的是一个实例或多个实例存在相互依赖的关系(类之间循环嵌套引用)。 举例: Component public class AService {// A中注入了BAutowiredprivate BService bService; }Component public class BService {// B中也…...
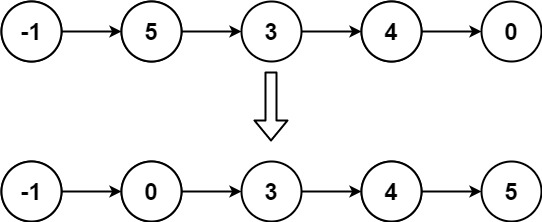
【数据结构与算法 | 灵神题单 | 插入链表篇】力扣2807, LCR 029, 147
1. 力扣2807:在链表中插入最大公约数 1.1 题目: 你一个链表的头 head ,每个结点包含一个整数值。 在相邻结点之间,请你插入一个新的结点,结点值为这两个相邻结点值的 最大公约数 。 请你返回插入之后的链表。 两个…...

瑞芯微rv1126 Linux 系统,修改系统时区,包有效方法
在 Linux 系统中,修改时区的步骤通常包括创建符号链接到正确的时区文件,并确保相关的配置文件已正确更新。然而,某些系统可能有额外的步骤或需要修改其他配置文件来使更改生效。以下是一些步骤。 1. 创建符号链接 ln -sf /usr/share/zoneinfo/Asia/Hong_Kong /etc/localti…...

系统架构设计师:数据库设计
简简单单 Online zuozuo: 简简单单 Online zuozuo 简简单单 Online zuozuo 简简单单 Online zuozuo 简简单单 Online zuozuo :本心、输入输出、结果 简简单单 Online zuozuo : 文章目录 系统架构设计师:数据库设计前言数据库基础概念数据模型三要素数据库的三级模型和两级…...

代码随想录刷题day31丨56. 合并区间,738.单调递增的数字,总结
代码随想录刷题day31丨56. 合并区间,738.单调递增的数字,总结 1.题目 1.1合并区间 题目链接:56. 合并区间 - 力扣(LeetCode) 视频讲解:贪心算法,合并区间有细节!LeetCode&#x…...
深圳建站公司-如何做网站
深圳建站公司:如何制作一个成功的网站 在信息化快速发展的今天,企业和个人越来越重视网络形象,网站成为了展示品牌、推广产品和服务的重要平台。深圳作为科技创新和经济发展的前沿城市,涌现出许多专业的建站公司,能够为…...
——随时间推移的降雨趋势案例分析(大规模气候监测))
Google Earth Engine(GEE)——随时间推移的降雨趋势案例分析(大规模气候监测)
简介 探索 Google Earth Engine环境类型中不同的数据。到目前为止,我们主要使用光学卫星数据,并探索了植被随时间和空间的趋势。然而,仅仅跟踪植被特性的变化并不足以了解是什么驱动了它们——我们需要能够将这些动态与其他环境数据联系起来。 在交互式 GEE 控制台中为您感…...

从新手到高手:用这9个策略让ChatGPT成为你的私人顾问!
ChatGPT已经出来快一年多了,但是我发现周围的小伙伴还是处在调戏ChatGPT的阶段,并没有在日常工作和生活中发挥他应由的价值。我调研下来发现最关键的痛点就是:不知道该怎么写Prompt可以让ChatGPT输出期望的回答。 哎吆,这不正是撞…...

高精度定位系统中的关键技术:GGA、EHP、RTMC、IMU、GNSS、INS 和 RTK 的协同工作
文章目录 0. 概述1. GGA:标准的定位数据格式2. EHP:增强高度精度3. RTMC:实时监控与控制4. IMU 和 INS:惯性测量和导航系统5. GNSS:全球导航卫星系统6. RTK:实时动态差分定位7. 各技术的融合与协同GPS 数据…...

Spring3~~~
目录 多例 后置处理器BeanPostProcessor XML配置 通过注解 AOP与后置处理器 JdbcTemplate jdbc.properties jdbc.xml Test 具名参数 DAO 声明式事务 GoodsDao GoodsService xml 传播机制 种类 隔离级别 超时回滚 如果是普通的java项目,xml文件放…...
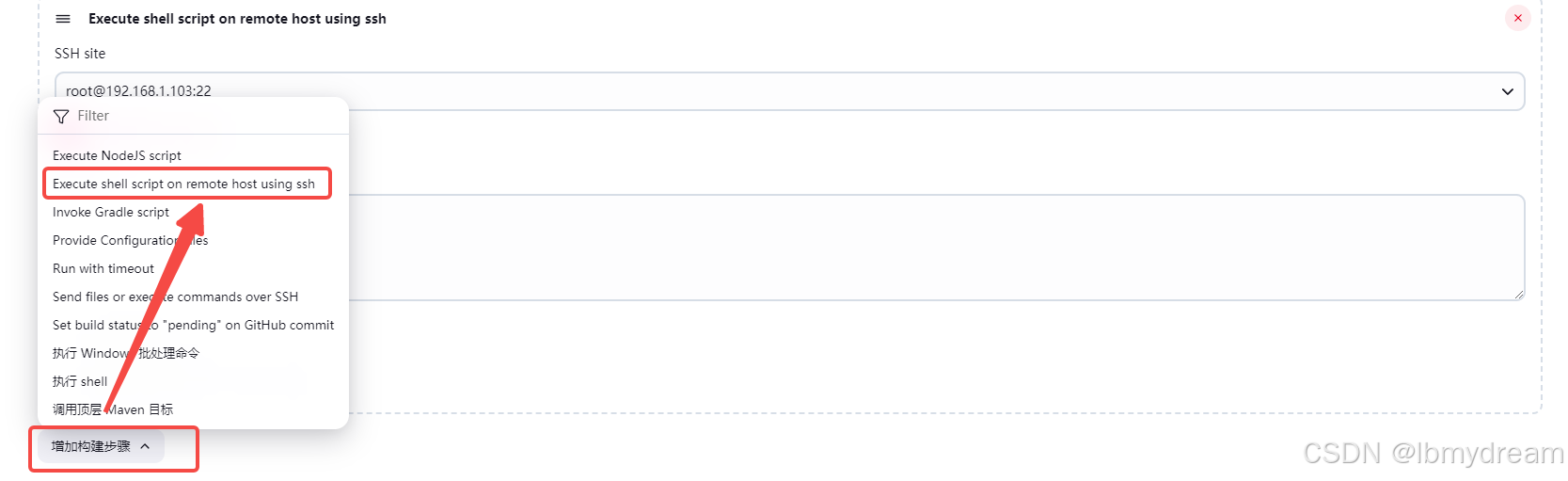
微服务CI/CD实践(五)Jenkins Docker 自动化构建部署Java微服务
微服务CI/CD实践系列: 微服务CI/CD实践(一)环境准备及虚拟机创建 微服务CI/CD实践(二)服务器先决准备 微服务CI/CD实践(三)Jenkins部署及环境配置 微服务CI/CD实践(四)…...

泰州高新区法院多层面强化固定资产管理
固定资产管理是法院的一项基础性工作,法院经费支出相当一部分用于固定资产的购置,为了提高固定资产使用质效,为执法办案提供坚实的保障,高新区法院积极探索科学合理的固定资产管理策略,更新管理思想,完善管…...

JDBC简介与应用:Java数据库连接的核心概念和技术
简短介绍 JDBC 及其重要性。 简短介绍 JDBC JDBC(Java Database Connectivity)是一种用于执行 SQL 语句的 Java API 并且独立于特定的数据库厂商。它允许开发者以一种标准的方式从 Java 应用程序中访问关系型数据库,这意味着一旦你掌握了 J…...

倒反天罡!这个AI风格模型可自由训练,还能批量生成同风格图像
在AIGC的新纪元中,模型已晋升为与算力并驾齐驱的生产力核心要素。也有不少用户反馈提到,如何利用神采PromeAI训练属于自己的风格模型?这需求必须安排!神采PromeAI「一致性模型」正式上线! 可自主训练风格化模型&#x…...

Stable Diffusion绘画 | ControlNet应用-Inpaint(局部重绘):更完美的重绘
Inpaint(局部重绘) 相当于小号的AI版PS,不但可以进行局部画面的修改,还可以去除背景中多余的内容,或者是四周画面内容的扩充。 预处理器说明 Inpaint_Global_Harmonious:重绘-全局融合算法,会对整个图片的画面和色调…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...
